PID-PID控制器參數整定與實現
2020-05-12 11:30:36
時Dout會有非常尖的尖峰,這時就要對delError進行限幅。在PID調節中,不允許出現很大的尖峰。 調好D后,NowVal會很好的跟隨TargetVal的變化而變化。 三、看圖整定參數 1-7
2020-06-23 14:54:44
PID參數的意義與整定方法資料
2015-07-31 09:17:31
PID溫度控制參數整定的方法是什么?
2021-11-22 06:13:41
怎么才能實現一個PID自整定
2023-10-12 07:46:15
PID算法及參數自整定在溫控系統中的實現
2009-03-14 17:06:09
第1章 概述 1.1 人工神經網絡研究與發展 1.2 生物神經元 1.3 人工神經網絡的構成 第2章人工神經網絡基本模型 2.1 MP模型 2.2 感知器模型 2.3 自適應線性
2012-03-20 11:32:43
將神經網絡移植到STM32最近在做的一個項目需要用到網絡進行擬合,并且將擬合得到的結果用作控制,就在想能不能直接在單片機上做神經網絡計算,這樣就可以實時計算,不依賴于上位機。所以要解決的主要是兩個
2022-01-11 06:20:53
神經網絡算法怎么去控制溫控系統,為什么不用pid控制
2023-10-27 06:10:14
求一個simulink的蓄電池用BP神經網絡PID控制電機加速勻速減速運動的模型仿真
2020-02-22 02:17:03
FPGA加速的關鍵因素是什么?EdgeBoard中神經網絡算子在FPGA中的實現方法是什么?
2021-09-28 06:37:44
【Simulink】FOA優化算法整定PID控制器參數(五)—— 一階帶時延的被控對象目錄【Simulink】FOA優化算法整定PID控制器參數(五)—— 一階帶時延的被控對象0研究背景1研究背景2
2021-08-30 06:46:44
如何去實現STM32電機的PID參數整定?如何去編寫STM32電機的PID參數整定的代碼?
2021-09-23 08:07:13
請問:我在用labview做BP神經網絡實現故障診斷,在NI官網找到了機器學習工具包(MLT),但是里面沒有關于這部分VI的幫助文檔,對于”BP神經網絡分類“這個范例有很多不懂的地方,比如
2017-02-22 16:08:08
各位大神,串級PID整定先后?發散振蕩該如何整定?
2017-05-14 10:15:36
語言,使用numpy.dot方法即可計算矩陣乘法。 以上便是一個簡單神經網絡的基本原理,對神經網絡有了基本的認識之后,我們才能進行復雜的神經網絡設計。總結本文講解了神經網絡的基本概念及其工作原理,利用
2019-03-03 22:10:19
今天學習了兩個神經網絡,分別是自適應諧振(ART)神經網絡與自組織映射(SOM)神經網絡。整體感覺不是很難,只不過一些最基礎的概念容易理解不清。首先ART神經網絡是競爭學習的一個代表,競爭型學習
2019-07-21 04:30:00
本文主要介紹PID參數的作用原理,參數整定的經典計算方法,通過看曲線整定PID參數的方法,串級控制、純滯后對象。回復帖子查看資料下載鏈接:[hide][/hide]
2021-08-05 10:10:47
為了方便大家查找技術資料,電子發燒友小編為大家整理一些精華資料,讓大家可以參考學習,希望對廣大電子愛好者有所幫助。
1.人工神經網絡算法的學習方法與應用實例(pdf彩版)
人工神經 網絡
2023-09-13 16:41:18
人工神經網絡(Artificial Neural Network,ANN)是一種類似生物神經網絡的信息處理結構,它的提出是為了解決一些非線性,非平穩,復雜的實際問題。那有哪些辦法能實現人工神經網絡呢?
2019-08-01 08:06:21
簡單理解LSTM神經網絡
2021-01-28 07:16:57
優化神經網絡訓練方法有哪些?
2022-09-06 09:52:36
全連接神經網絡和卷積神經網絡的區別
2019-06-06 14:21:42
一直以來,關于PID整定都在進行手動調試,例如試湊法、1/4衰減曲線法、齊格勒-尼柯爾斯整定法等; 雖然上述方法都可以完成對參數的整定,但是需要非常豐富的調試經驗才能達到預期的目的。同時,當需要控制
2021-08-31 08:41:30
這種情況是怎么回事;求教下相關PID參數整定方法,涉及到溫度控制方面的。另外通過Autotunning PID參數調出PID整定向導,整定出來的參數在控制過程中,效果也不太好。
2015-05-05 16:20:33
PID參數整定有什么作用?分享一些基于直流電機調速平臺的PID參數整定經驗
2021-06-30 06:42:04
卷積神經網絡(CNN)究竟是什么,鑒于神經網絡在工程上經歷了曲折的歷史,您為什么還會在意它呢? 對于這些非常中肯的問題,我們似乎可以給出相對簡明的答案。
2019-07-17 07:21:50
卷積神經網絡模型發展及應用轉載****地址:http://fcst.ceaj.org/CN/abstract/abstract2521.shtml深度學習是機器學習和人工智能研究的最新趨勢,作為一個
2022-08-02 10:39:39
卷積神經網絡的層級結構 卷積神經網絡的常用框架
2020-12-29 06:16:44
什么是卷積神經網絡?ImageNet-2010網絡結構是如何構成的?有哪些基本參數?
2021-06-17 11:48:22
.模糊參數自整定PID控制器的設計與仿真研究[J].中原工學院學報, 20O7,18(1):65-67 [5] 劉學東.模糊自整定PID控制器參數的設計[J].河北理工學院學報,2004,26(1
2019-04-17 09:40:02
轉速環,內環為電流環。本次轉速調節器采用基于BP神經網絡PID控制器,其參數由神經網絡自學習調整得到,從而克服系統運行過程中各種不利因素對系統所造成的影響,以達到較好的控制效果。電...
2021-06-28 12:03:44
神經網絡可以建立參數Kp,Ki,Kd自整定的PID控制器。基于BP神經網絡的PID控制系統結構框圖如下圖所示:控制器由兩部分組成:經典增量式PID控制器;BP神經網絡...
2021-09-07 07:43:47
FPGA實現神經網絡關鍵問題分析基于FPGA的ANN實現方法基于FPGA的神經網絡的性能評估及局限性
2021-04-30 06:58:13
如何用stm32cube.ai簡化人工神經網絡映射?如何使用stm32cube.ai部署神經網絡?
2021-10-11 08:05:42
原文鏈接:http://tecdat.cn/?p=5725 神經網絡是一種基于現有數據創建預測的計算系統。如何構建神經網絡?神經網絡包括:輸入層:根據現有數據獲取輸入的層隱藏層:使用反向傳播優化輸入變量權重的層,以提高模型的預測能力輸出層:基于輸入和隱藏層的數據輸出預測
2021-07-12 08:02:11
神經網絡(Neural Networks)是人工神經網絡(Ar-tificial Neural Networks)的簡稱,是當前的研究熱點之一。人腦在接受視覺感官傳來的大量圖像信息后,能迅速做出反應
2019-08-08 06:11:30
作者:李云紅0 引言自20世紀70年代以來,模擬電路故障診斷領域已經取得了一定的研究成果,近年來,基于神經網絡技術的現代模擬電路軟故障診斷方法已成為新的研究熱點,神經網絡的泛化能力和非線性映射能力
2019-07-05 08:06:02
PID調節器參數整定方法很多,常見的工程整定方法有臨界比例度法、衰減曲線法和經驗法。本帖以圖文形式分別介紹調節器參數整定方法。調節器參數 yunrun.com.cn/tech/440.html臨界
2017-12-26 21:40:51
通常是用什么算法實現自整定的
2023-10-23 06:08:41
怎樣去整定PID的參數呢?PID參數的整定方法有哪幾種?有哪位大神遇到過這個問題
2021-07-06 06:01:03
轉帖用經驗法整定調節器參數又稱為試湊法,是廣大儀表工數十年整定經驗的積累,是應用最為廣泛的一種調節器參數整定方法。它就是根據儀表工的經驗及控制過程的曲線形狀,直接對控制系統反復地、逐漸地試湊,最終
2017-11-14 09:06:47
吳恩達機器學習筆記之神經網絡參數的反向傳播算法
2019-05-22 15:11:21
求一個simulink的蓄電池用BP神經網絡PID控制電機加速勻速減速運動的模型仿真
2020-02-22 02:15:50
求一個基于BP神經網絡PID控制器應用于雙閉環直流調速系統BP_PID控制器學習參數怎么設置?
2021-10-13 08:10:12
小女子做基于labview的蒸發過程中液位的控制,想使用神經網絡pid控制,請問這個控制方法可以嗎?有誰會神經網絡pid控制么。。。叩謝
2016-09-23 13:43:16
小弟試過了用labview里的pid例程里的Plant作為被控對象,但是自整定不成功,求高手幫忙,謝謝
2012-04-25 09:19:52
淺談增量式PID參數整定https://bbs.elecfans.com/jishu_260252_1_1.html
2012-08-18 09:50:39
PID yunrun.com.cn/tech/681.html用經驗法整定PID參數又稱為試湊法,是廣大儀表工數十年整定經驗的積累,是應用最為廣泛的一種調節器參數整定方法。它就是根據儀表工的經驗
2018-01-04 21:07:26
自己整理的PID工程整定方法
2020-05-26 09:14:46
如何去設計模糊PID自整定控制器?關于模糊控制器算法的研究是什么?模糊PID控制器具有哪些特點?
2021-04-21 06:08:28
各位大神,請問有沒有編過模糊PID控制程序或神經網絡控制程序?
2015-01-12 10:50:48
,就引入參數自整定的概念。實質就是在首次使用時,通過 N 次測量為新的工作對象尋找一套參數,并記憶下來作為以后工作的依據。具體的整定方法有三種:臨界比例度法、衰減曲線法、經驗法。1、臨界比例度法
2020-02-23 07:00:00
PID參數的虛擬控制器。將此控制器用于時控系統,控制效果理想,魯棒性強。關鍵詞:模糊參數自整定PID MATLAB Simulink 基于LabVIEW與MATLAB的模糊參數自整定PID控制.pdf
2019-04-03 09:40:03
有關神經網絡PID 控制的文獻中使用的大都是PID 的一般控制算法,而性能相對優于一般PID 控制算法的不完全微分PID算法則很少用于神經網絡控制中。神經網絡與不完全微分的PID 算
2008-12-20 15:13:58 20
20 有關神經網絡PID 控制的文獻中使用的大都是PID 的一般控制算法,而性能相對優于一般PID 控制算法的不完全微分PID算法則很少用于神經網絡控制中。神經網絡與不完全微分的PID 算法
2009-01-07 15:40:52 3
3 本文提出一種基于BP 神經網絡的新型智能PID 控制方法和一些BP 神經網絡的基本概念。同傳統的PID控制相比較,神經網絡智能PID 控制有許多優點。把BP 神經網絡的PID 控制方法應用
2009-05-26 11:19:36 34
34 應用仿人智能魯棒性高、能對付難控對象的控制特點,結合模糊RBF 神經網絡控制技術,提出仿人模糊神經網絡控制方法,對PID 控制器參數進行優化調節。該方法采用仿人智能的
2009-06-09 10:47:36 17
17 提出利用CMAC 神經網絡與PID 的復合控制,實現非線性系統控制。由于CMAC 網絡的優點使PID 控制效果有很大提高。仿真實驗表明了該方法的有效性。關鍵詞:神經網絡;PID 控制;非
2009-06-11 09:16:51 23
23 設計了一種基于神經網絡結構的模糊控制器,并將它與PID 控制器相結合,動態的調整PID 參數。系統根據技術人員的經驗和知識,離線的進行學習,使得模糊神經網絡掌握調節PID 參
2009-06-15 09:39:38 12
12 為了消除造紙工業抄紙過程中存在的解耦問題,提出了一種基于PID 神經網絡的解耦方法。文章在介紹PID 神經網絡原理的基礎上,給出了二變量PID 神經元網絡解耦控制系統結構圖,
2009-06-15 10:10:47 19
19 闡述了CMAC 神經網絡的基本原理,并結合PID 控制的特點,將CMAC 神經網絡與PID 復合控制算法應用在工業領域的溫度控制系統中,并同傳統的Zieglar-Nichols 階躍響應法及單純形算法作了
2009-06-20 09:21:36 17
17 將神經網絡和PID 控制相結合,提出了一種基于對角遞歸神經網絡整定的PID 控制策略,并將其應用于交流伺服系統的控制。利用對角遞歸神經網絡在線自適應調整PID 控制器的參數,
2009-07-30 09:40:12 10
10 本文介紹了小腦模型神經網絡CMAC的原理及基于CMAC與PID的并行控制設計,以及該設計在換熱器控制中的應用,并對該設計在MATLAB下進行了仿真,得到了較好的控制效果。 關鍵詞:小
2009-08-03 11:41:32 10
10 為了改善工業控制系統的動態調節品質,運用BP 神經網絡控制算法設計了一種神經網絡PID 控制器,并給出了基于西門子PLC 的神經網絡PID 控制器的實現方法,仿真和實驗結果表明
2009-08-10 11:12:32 42
42 本文討論了使用BP 神經網絡PID 控制算法,并且將這種控制算法應用在漂白工段的控制當中。利用神經網絡自學習能力,在線整定PID 控制參數。實踐證明BP 神經網絡PID控制器具有
2009-08-15 10:27:36 34
34 在小腦神經網絡(CMAC)與PID 并行控制的基礎上,提出了一種新型的CMAC 控制器,即CMAC 控制器。這種把小腦神經網絡與模糊控制(Fuzzy)結合起來的控制方法,具有兩種控制方法的優
2009-09-12 16:09:36 16
16 本文討論了神經網絡PID 控制策略,利用神經網絡的自學習能力進行PID控制參數的在線整定,并使用Matlab 軟件進行了仿真研究。仿真結果表明,神經網絡PID 控制器參數調整簡單,具
2009-09-14 16:53:35 60
60 應用仿人智能魯棒性高、能對付難控對象的控制特點,結合模糊RBF 神經網絡控制技術,提出仿人模糊神經網絡控制方法,對PID 控制器參數進行優化調節。該方法采用仿人智能的
2009-12-19 11:50:03 12
12 在小腦神經網絡(CMAC)與PID并行控制的基礎上,提出了一種新型的CMAC控制器,即FCMAC控制器。這種把小腦神經網絡與模糊控制(Fuzzy)結合起來的控制方法,具有兩種控制方法的優
2010-07-20 15:41:58 10
10 詳細介紹了CMAC神經網絡結構" 中間層作用函數地址的計算方法" 輸出層權值的學習算法# 并利用CMAC神經網絡對水下機器人深度模糊控制器進行了學習$ 仿真結果表明% 訓練得到的
2010-07-22 15:49:59 25
25 【摘要】基于神經網絡實現智能PID控制的策略,它以經典的PID控制為基礎,通過神經網絡參數整定實現,進而進行自學,用于多變量系統的解耦控制。本文給出了網絡的結構和算法,對
2010-08-25 11:09:34 29
29 基于FPGA的人工神經網絡實現方法的研究
引 言 人工神經網絡(Artificial Neural Network,ANN)是一種類似生物神經網絡的信息處理結構,它的提出是為了
2009-11-17 17:17:20 1119
1119 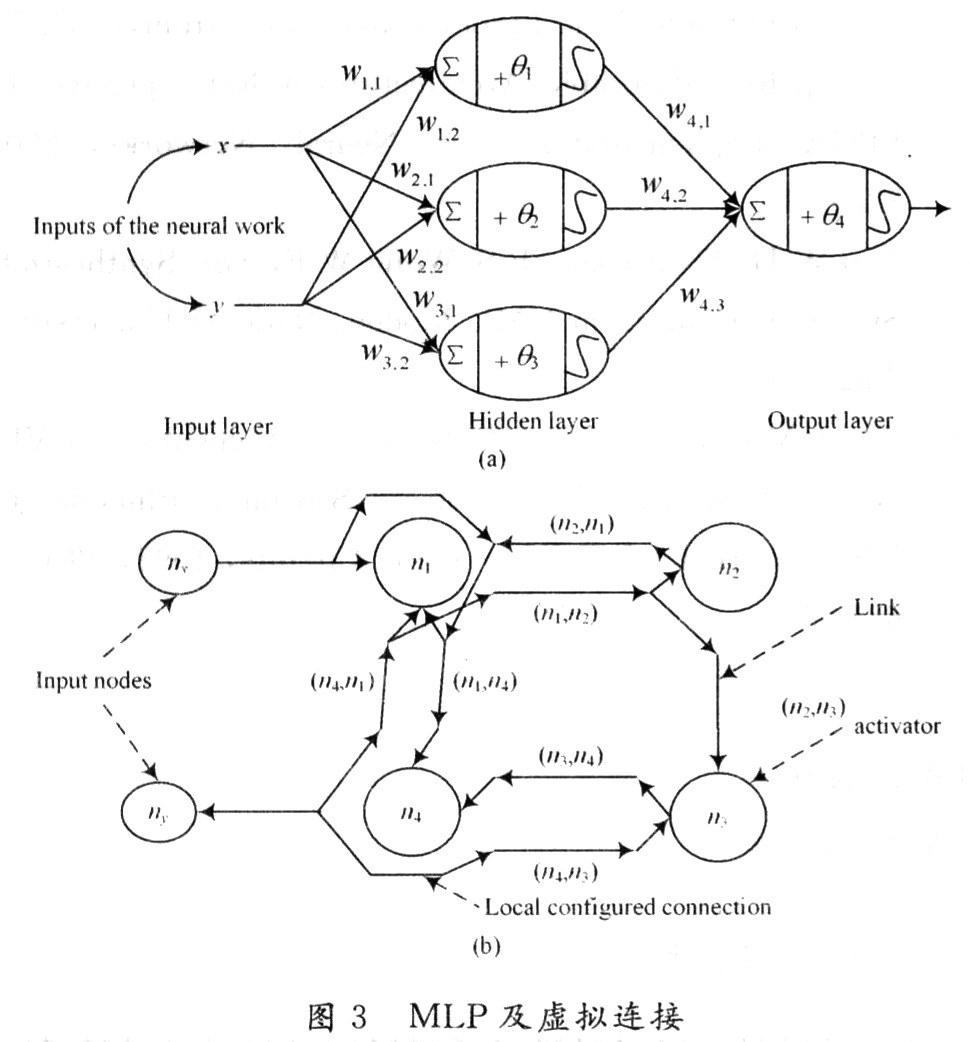
基于FPGA的人工神經網絡實現方法的研究
引言
人工神經網絡(ArtificialNeuralNetwork,ANN)是一種類似生物神經網絡的信息處理結構,它的提出是為了解決一些非線
2009-11-21 16:25:24 4633
4633 近年來,由于神經網絡的研究取得了長足的進展,基于BP神經網絡模型的速度辨識方法得到了廣泛研究,但其仍存在收斂速度慢、易陷入局部極小值等問題,因此,對神經網絡的優化
2010-06-14 06:52:32 1105
1105 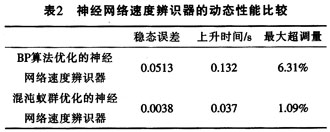
應用
CMAC神經網絡具有小腦的機能,因而,被廣泛應用于機器人的運動控制。或者反過來說,正是為了機器人的運動控制,Albus構造了CMAC神經系統,以模擬脊椎動物
2010-08-09 14:57:16 1443
1443 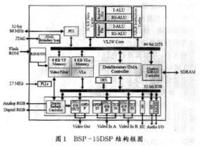
基于RBF神經網絡整定PID的風力發電變槳距控制
2011-10-14 15:42:39 25
25 針對傳統PID控制系統參數整定過程存在的在線整定困難和控制品質不理想等問題,結合BP神經網絡自學習和自適應能力強等特點,提出采用BP神經網絡優化PID控制器參數。其次,為了加快
2012-03-20 10:50:04 44
44 基于BP神經網絡的PID控制器的研究與實現:
2012-04-01 15:20:51 15
15 文中將BP神經網絡的原理應用于參數辨識過程,結合傳統的 PID控制算法,形成一種改進型BP神經網絡PID控制算法。該算法利用BP神經網絡建立系統參數模型,能夠跟蹤被控對象的變化,取
2012-07-16 15:53:08 51
51 基于神經網絡的聚類方法研究_胡偉
2017-03-16 09:37:53 0
0 PID 控制算法簡單、應用廣泛,既能消除余差,又能提高系統的穩定性,但其P 環節、I 環節、D 環節的控制參數卻參數難以整定;BP 神經網絡算法具有很強的數字運算能力,因此,可通過BP 神經網絡
2019-10-11 16:06:48 38
38 圖1顯示了模糊CMAC神經網絡的結構和運算過程。模糊CMAC神經網絡可以用于近似一個非線性映射y(x):Xn→Ym,其中Xn∈Rn是在n維輸入空間中的應用,Ym“∈Rm是在m維輸出空間中的應用[1,2]。模糊CMAC算法由決定一個復雜函數值的兩個初等函數組成,如圖1所示。
2020-04-25 17:30:00 1465
1465 
通過對傳統BP神經網絡缺點的分析,從參數選取、BP算法、激活函數、網絡結構4個方面綜述了其改進方法。介紹了各種方法的原理、應用背景及其在BP神經網絡中的應用,同時分析了各種方法的優缺點。指出不斷提高網絡的訓練速度、收斂性和泛化能力仍是今后的研究方向,并展望了BP神經網絡的研究重點。
2021-06-01 11:28:43 5
5


 ?),再將所得參數送入PID控制器,從而實現PID參數的自整定。PID參數自整定系統如圖3所示。
?),再將所得參數送入PID控制器,從而實現PID參數的自整定。PID參數自整定系統如圖3所示。


 ?,原控制器對此對象的控制性能達到要求,階躍擾動曲線如圖8中線1所示。當進行PID參數自整定,整定后的響應曲線為圖8中線2,把特征參量送入CMAC參數整定網絡,整定后參數為
?,原控制器對此對象的控制性能達到要求,階躍擾動曲線如圖8中線1所示。當進行PID參數自整定,整定后的響應曲線為圖8中線2,把特征參量送入CMAC參數整定網絡,整定后參數為 。從仿真圖中,我們可以看出PID參數的整定效果比較理想,且CMAC神經網絡的達到穩定的訓練時間也比較短。
。從仿真圖中,我們可以看出PID參數的整定效果比較理想,且CMAC神經網絡的達到穩定的訓練時間也比較短。 電子發燒友App
電子發燒友App
























評論