引言

變?nèi)莨苁菈嚎?a target="_blank">振蕩器、調(diào)頻器、鎖相環(huán)等電路的關(guān)鍵部件。傳統(tǒng)的分立電子線路常采用特制的二極管作為變?nèi)莨埽貌牧隙酁楣杌蛏榛墕尉В⒉捎猛庋庸に嚰夹g(shù)。自動頻率控制（AFC）和調(diào)諧所用的小功率變?nèi)荻O管通常采用硅的擴(kuò)散型二極管，也采用合金擴(kuò)散、外延結(jié)合、雙重?cái)U(kuò)散等特殊工藝制作。作為壓控器件，這些傳統(tǒng)變?nèi)荻O管的品質(zhì)因數(shù)很小，并且工藝也有特別的要求。這將不便和CMOS工藝兼容從而限制了它在CMOS模擬集成電路中的應(yīng)用。因而，研究用CMOS工藝制作具有變?nèi)萏匦缘腗OS管代替一般變?nèi)荻O管是普通工藝下IC設(shè)計(jì)很有意義的一項(xiàng)工作。雖然，人們對MOS電容的壓控變?nèi)萏匦赃M(jìn)行了廣泛而深入的研究，但對CMOS工藝集成的PMOS作變?nèi)莨艿难芯坎⒉欢嘁姟１疚尼槍MOS工藝下的PMOS壓控變?nèi)萏匦赃M(jìn)行研究，并對其高頻交變壓控特性建模，為CMOS工藝兼容高頻電路的晶體管級仿真提供簡化模型。

1 MOS結(jié)構(gòu)電容的壓控特性分析

1．1 理想MIS結(jié)構(gòu)電容的壓控特性

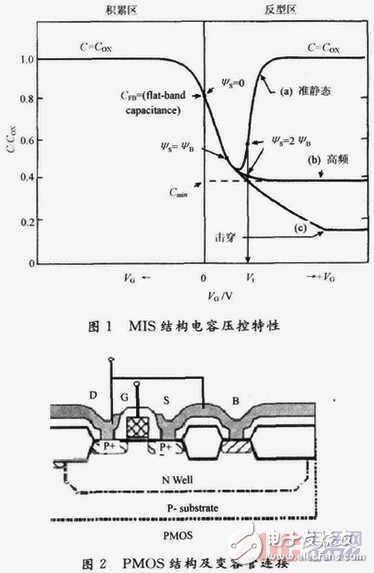
根據(jù)半導(dǎo)體表面電場效應(yīng)，通常按照多子堆積狀態(tài)、多子耗盡狀態(tài)及少子反型狀態(tài)3種彼此孤立的理想情況對MIS結(jié)構(gòu)電容的壓控特性進(jìn)行理論分析。但實(shí)際上，3種情況間出現(xiàn)過渡過程，如堆積狀態(tài)與耗盡狀態(tài)間經(jīng)過有平帶狀態(tài)、耗盡狀態(tài)過渡到反型狀態(tài)經(jīng)歷弱反型直至強(qiáng)反型態(tài)，所以其壓控特性是連續(xù)變化的。倘若交變電壓頻率較高時，反型層中少子的產(chǎn)生與復(fù)合跟不上外電場的變化，其數(shù)量基本不變、空間電荷區(qū)的電容仍然由耗盡區(qū)的電荷變化決定的。因此，在反型區(qū)內(nèi)電容的壓控特性有準(zhǔn)靜態(tài)和高頻情形之區(qū)別，如圖1所示。

1．2 PMOS的變?nèi)莨苓B接及其壓控特性分析

圖2為PMOS管連接成壓控可變電容的示意圖。具體是將漏、源和襯底短接作為電容的一極接高電平，柵極作為另一極接低電平。這種連接與MIS電容結(jié)構(gòu)有著類似的機(jī)理，所以，電容值隨襯底與柵極之間的電壓VBG變化。

對于PMOS變?nèi)莨埽谝r柵電壓VBG的作用下，變?nèi)莨艿碾娙菘梢钥醋鳀叛趸瘜与娙菖c半導(dǎo)體空間電荷區(qū)電容的串聯(lián)，即：

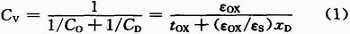
因?yàn)榉葱洼d流子溝道在VBG超過閾值電壓時建立，所以，當(dāng)VBG遠(yuǎn)遠(yuǎn)超越閾值電壓時，變?nèi)莨芄ぷ髟趶?qiáng)反型區(qū)域；在柵電位VG大于襯底電位VB時，變?nèi)莨苓M(jìn)入積累區(qū)，此時柵氧化層與半導(dǎo)體之間的界面電壓為正且足夠高使得電子可以自由移動。這樣，在反型區(qū)和積累區(qū)的變?nèi)莨艿碾娙葜担?/p>

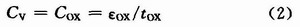
閾值反型點(diǎn)是當(dāng)達(dá)到最大耗盡寬度且反型層電荷密度為零時得到的最小電容：

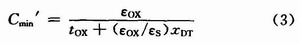
平帶是發(fā)生在堆積和耗盡模式間，電容為：

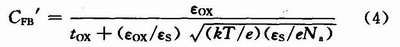
式（1）～式（4）中牽扯到的各參量的意義分別為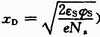：為耗盡層的厚度，εs是半導(dǎo)體的介電常數(shù)、φs稱為表面勢；Na為受主原子的濃度；e為基本電荷的電量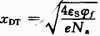；為反型轉(zhuǎn)折點(diǎn)的空間電荷區(qū)最大寬度，φf=Vtln（Na／ni）為雜質(zhì)半導(dǎo)體襯底的相對費(fèi)米勢，Vt= kT／e為熱電壓，ni為本征載流子濃度，k為玻爾茲曼常數(shù)，T為絕對溫度；εox為氧化層的介電常數(shù)；tox為氧化層厚度。

由于處于耗盡區(qū)、弱反型區(qū)和中反型區(qū)3個區(qū)域中的PMOS只有很少的移動載流子，這使得PMOS電容Cv減小（比Cox小）。此時，Cv可以看成由氧化層電容Cox和半導(dǎo)體表面空間電荷層電容（由Cb與Ci的并聯(lián)電容值，Cb表示耗盡區(qū)域電容，而Ci與柵氧化層界面的空穴數(shù)量變化相關(guān)）串聯(lián)構(gòu)成，如式（1）所示。從反型載流子溝道建立開始到強(qiáng)反型區(qū)又可細(xì)分為3個工作區(qū)域：弱反型區(qū)、中反型區(qū)和強(qiáng)反型區(qū)。如果Cb（Ci）占主

導(dǎo)地位，則MOS器件工作在中反型（耗盡）區(qū)；如果2個電容都不占主導(dǎo)地位，MOS器件工作在弱反型區(qū)。

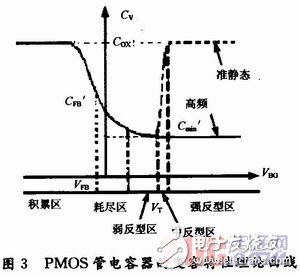
進(jìn)入強(qiáng)反型區(qū)后分為高頻和低頻兩種測試情形，高頻條件下少數(shù)載流子的產(chǎn)生與復(fù)合均跟不上信號的變化，于是Cv不隨偏壓的變化；而低頻（準(zhǔn)靜態(tài)）下它能隨偏壓而變化。理論上，常常在各區(qū)段抓住影響MOS管電容Cv的主要因素進(jìn)行研究，但各個次要因素與主要因素相互作用，構(gòu)成連續(xù)的變?nèi)萏匦郧€如圖3所示。可見，PMOS管電容器的變?nèi)萏匦岳碚撉€與一般MIS結(jié)構(gòu)電容的特性變化趨勢相似。

2 PMOS管變?nèi)萏匦越Ｅc仿真

2．1 PMOS管變?nèi)莞哳l特性建模

用HSpice和Candence Spectre進(jìn)行晶體管級電路模擬仿真時，軟件根據(jù)晶體管靜態(tài)條件下所建模型對PMOS變?nèi)莨軠?zhǔn)靜態(tài)特性的獲取較為方便，但對其高頻特性顯得無能為力。以下將基于PMOS變?nèi)莨軠?zhǔn)靜態(tài)特性的基本參數(shù)，采用特性曲線擬合的辦法，對PMOS變?nèi)莨芨哳l（即動態(tài)）特性進(jìn)行建模。

由圖3可見，Cv隨VBG變化的高頻特性曲線類似于雙曲正切函數(shù)曲線，選取曲線的關(guān)鍵點(diǎn)（-∞，Cox）、（VT，Cmin’）并引入電容變化指數(shù)γ（類似于變?nèi)荻O管的結(jié)電容變化指數(shù)）與此特性曲線進(jìn)行擬合，得PMOS管高頻變?nèi)軻BG～CV特性的模型函數(shù)：

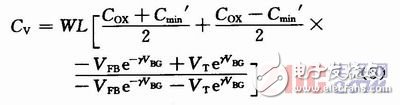
2．2 PMOS管變?nèi)萏匦苑抡?/h3>

2．2．1 變?nèi)莨軠?zhǔn)靜態(tài)特性的Hspice仿真

為獲得式（5）中所需的基本參數(shù)，且便于和理論分析的特性曲線作對比，選取Charted 0．35μm工藝庫，用Hspiee對PMOS管連接的變?nèi)萜髋c以固定電容器相串聯(lián)，離散加入一系列靜態(tài)偏壓，根據(jù)分壓逐一地得到PMOS變?nèi)萜鞯娜葜岛蛯?yīng)的偏壓。仿真時，PMOS管尺寸取L=1μ，W=7．1μm，得到逐點(diǎn)仿真的準(zhǔn)靜態(tài)擬合曲線如圖4所示。

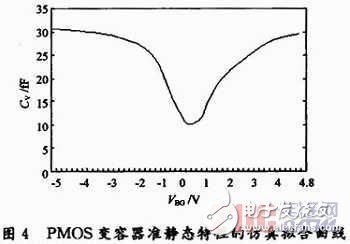
這個曲線的走勢與理論分析的變化趨勢一致。

2．2．2 變?nèi)莨芨哳l特性的Matlab仿真

取L=1μm，分別對W=7．1μm，W=4．3 μm兩種情形用Matlab仿真。其他參數(shù)為：εs=11.7×8．854×10-12F／m，γ=1／2，VFB=-1．95V，Na=5×1021m-3，ni=1.5×1014m-3，tox=7.46×10-9m，絕對溫度T為300K，VT=-0.8427V，e為基本電荷的電量；εox=3.9×8.854×10-12 F／m。仿真得到的PMOS變?nèi)萜鞲哳l特性VBG—CV曲線如圖5所示。可見，不同尺寸的PMOS變?nèi)莨埽渥畲蟆⒆钚‰娙萦袆e，隨WL的增大二者均有所增大，相當(dāng)于極板正對面積增大。這就是設(shè)計(jì)中確定變?nèi)莘秶囊罁?jù)。

2．2．3 變?nèi)萏匦苑抡娼Y(jié)果的對比

為了說明所建模型的正確性，將尺寸為L=1 μm，W=7．1μm的PMOS管用HSpice仿真的準(zhǔn)靜態(tài)變?nèi)萏匦郧€與用Matlab分別仿真L=1μm時W=

7．1μm，W=4．3 μm的高頻變?nèi)萏匦郧€放在同一VBG—CV坐標(biāo)上比較，如圖6所示。

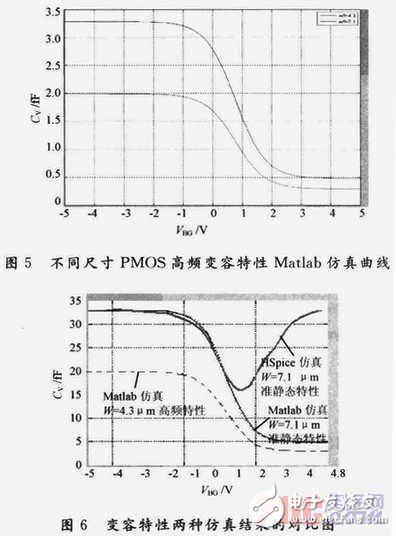
可見，PMOS變?nèi)萏匦栽跍?zhǔn)靜態(tài)與高頻特性分離以前曲線吻合得很好。由于HSpiee仿真與具體工藝參數(shù)相結(jié)合，可以認(rèn)為仿真曲線為實(shí)際準(zhǔn)靜態(tài)特性，而用Matlab對高頻模型仿真所得到的高頻變?nèi)萏匦郧€為模型曲線。并且二者共同完成了對PMOS電容器連接的變?nèi)萏匦悦枋觯浣Y(jié)果和分析結(jié)果與圖2一致。

3 結(jié)語

本文對PMOS用作變?nèi)莨軙r的特性進(jìn)行了研究，用HSpice對準(zhǔn)靜態(tài)特性進(jìn)行仿真描繪，從而確定了一些關(guān)鍵點(diǎn)。在此基礎(chǔ)上，建立了高頻變?nèi)萏匦缘暮喕Ｐ停肕atlab對模型進(jìn)行了仿真，并與HSpice得到的準(zhǔn)靜態(tài)結(jié)果局部比對、與理論分析總體比對均說明了結(jié)果的正確性。

該模型補(bǔ)充了與CMOS工藝兼容的變?nèi)莨茉O(shè)計(jì)時在高頻情況下的仿真問題；它能夠描述管子壓控變?nèi)蒿@著區(qū)段的變化規(guī)律。此模型算法可以嵌入到仿真工具里，較為準(zhǔn)確地反映控制電壓信號的頻率在10 kHz以上變?nèi)莨芴匦裕会槍Σ煌腃MOS工藝，修改變?nèi)葜笖?shù)即可，因而，此模型有普遍的適用性和較強(qiáng)的移植性。