ITU-T G.701標準對抖動的定義為：“抖動是指數字信號在短期內重要的瞬時變化相對于理想位置發生的偏移”。

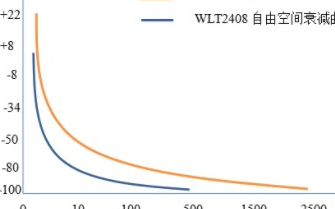
　　還有一個跟抖動很類似的概念，即漂移。一般情況下，抖動是指發生得比較快的定時偏差，而漂移是指發生的比較慢得定時偏差。ITU把漂移和抖動之間的門限定義為10Hz，偏移頻率大于10Hz的叫抖動，小于10Hz的叫做漂移。

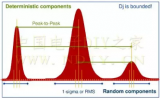
　　抖動可以分為隨機性抖動（RJ）和確定性抖動（DJ），而確定性抖動又可以分為周期性抖動（PJ）、數據相關抖動（DDJ）和占空比抖動（DCD）三種，如下圖所示：

　　縮略語：

　　TJ：Total Jitter 總抖動

　　DJ：Deterministic Jitter 確定性抖動

　　RJ：Random Jitter 隨機抖動

　　PJ：Periodic Jitter 周期性抖動

　　DDJ：Data Dependent Jitter 數據相關抖動

　　DCD：Duty Cycle Distortion 工作周期抖動

　　TIE：Time Interval Error 時間區間誤差

　　RMS：Root Mean Square 均方根

　　ISI：Inter Symbol Interference 碼間干擾

　　1.隨機抖動（RJ）

　　隨機抖動產生的原因很復雜，很難消除。器件的內部熱噪聲，晶體的隨機振動，宇宙射線等都可能引起隨機抖動。

　　隨機抖動滿足高斯分布，在理論上是無邊界的，只要測試的時間足夠長，隨機抖動也是無限大的。高斯分布概率密度函數圖形如下圖所示。

　　所以隨機抖動的鋒-鋒值必須伴同誤碼率BER表示出來，RJRMS＝概率密度函數（pdf）的標準偏差：σ，隨機抖動的鋒-鋒值RJpk-pk=N*σ，按不同的BER，N不同，如下圖所示：

　　2.確定性抖動（DJ）

　　確定性抖動不是高斯分布，通常是有邊際的，它是可重復可預測的。信號的反射、串擾、開關噪聲、電源干擾、EMI等都會產生DJ。DJ的概率密度函數圖形如下圖所示：

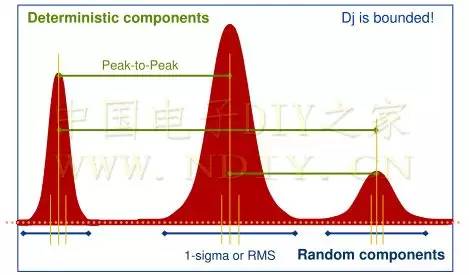
　　1）。周期性抖動（PJ）

　　以周期方式重復的抖動稱為周期性抖動，由于可以將周期波形分解為與諧波相關的正弦曲線的傅立葉級數，因此，這類抖動有時也稱為正弦抖動。周期抖動與數據流中任何定期重復的碼型無關，周期抖動一般是由耦合到系統中的外部確定的噪聲源引起的。可能的抖動源有：電源的EMI干擾與擴頻時鐘SSC的調制信號。

　　2）。數據相關抖動（DDJ）

　　DDJ一般是由于電纜或設備的帶寬限制及阻抗不匹配造成的。DDJ分為DCD和ISI兩種。

　　DCD值是相對于額定值50%的占空比偏差，一般分兩種情況：

　　①信號的上升沿和下降沿的斜率不同；

　　②信號DC平均值發生變化而導致波形的判決門限高/低于應有值；

　　ISI又稱為DDJ數據相關抖動或PDJ碼型相關抖動。

　　因為阻抗不匹配導致信號發射。被發射的信號疊加在原信號上導致信號幅度增加而最終使轉換電平所耗費的時間更多，從而產生抖動。對經常切換的“1，0，1，0…”高頻信號，其衰減比連續的“1，1，1，1，0，0，0，0…”低頻信號大。所以長的連續不變碼會到達更高的電平，在跳變時需要更多的時間才能到達門限電平，導致信號抖動。因為這個抖動的幅度與碼型相關，所以又稱碼型相關抖動。

　　總抖動鋒-鋒值：TJpk-pk=（N*RJRMS）+DJpk-pk

　　信號抖動值的測量主要分為時鐘、并行總線和高速串行數據三大類。時鐘抖動的測量指標有：Period Jitter （周期抖動），Cycle to Cycle Jitter （周期間抖動），N-Cycle Jitter （N個周期后抖動），TIE （時間間隔誤差）四種；并行總線以及其它所有的源同步數據總線中的數據與時鐘相關抖動的測量指標有：Setup/Hold time jitter（建立/保持時間抖動），Clk-out time jitter，Crossover Voltage Jitter（差分交點電壓抖動）三種；高速串行數據的抖動測量主要PLL TIE。

　　1）.Period Jitter

　　周期性抖動測量主要是針對時鐘信號，它測量實時時鐘的每一個周期，然后對實際時鐘周期進行數據統計，最后根據概率統計，給出該時鐘周期大小的分布規律，此測量將顯示信號的整體質量。測量Period Jitter必須指定一定的采樣周期數，不同的周期數，抖動的PK-PK值是不同的，JEDEC要求的采樣數最少為10000個。測量統計過程如下圖所示：

　　2）.Cycle to Cycle Jitter

　　Cycle to Cycle Jitter 是測量任意兩個相鄰周期間信號的周期變化量，通周期性抖動一樣，測量周期間抖動也必須指定一定的周期數才能確定抖動的鋒-鋒值，JEDEC中要求最少采樣1000個周期。測量統計過程如下圖所示：

　　3）。 N-Cycle Jitter

　　N個周期后抖動是測量由參考點滯后相當數量（N）個時鐘周期后沿的抖動，該參數描述的是抖動的積累效應。測量該指標時需要一個邊沿的統計常數為參考，否則測出來的抖動可能會大于一個UI。測量統計過程如下圖所示：

　　4）.TIE

　　TIE是通過使用參考時鐘或時鐘恢復提供理想邊沿，據此來測量時鐘或者數據的每個有效邊沿與理想位置的差距。TIE在通信系統中尤為重要，因為它顯示了一段時間內抖動的趨勢。下圖Period Jitter、Cycle to Cycle Jitter及TIE之間的關系：

　　三種抖動統計類型的趨勢圖如下所示：

　　5）.Setup/Hold Time Jitter

　　Setup/Hold Time Jitter主要測量信號相對了時鐘采樣邊沿的建立/保持時間波動情況，如下圖所示：

　　6）.Crossover Voltage Jitter

　　Crossover Voltage Jitter主要測量差分信號P端的上升沿與N端的交叉點波動情況，如下圖所示：

　　7）.Clk-out Time Jitter

　　這個抖動指標跟Setup/Hold Time Jitter類似，只不過Setup/Hold Time Jitter是相對于接收端而言的，而Clk-out Time Jitter是相對與發送端而言的。

　　8）.PLL TIE

　　該參數用于高速串行數據的抖動測試中，PLL TIE使用了Gloden PLL來進行時鐘恢復，將串行數據速率除以1667作為PLL的環路帶寬。

　　在實際測量中，我們經常會遇到RMS Jitter指標，實際上，RMS就是Root Mean Square（均方根），它等于概率分布密度函數的（pdf）的標準方差σ。

　　對于同時抖動的RMS值一般為pk-pk值的1/7。

　　抖動的分類

　　胡為東 美國力科公司上海代表處

　　2009年6月

　　【摘要】

　　本文簡要介紹了信號抖動在不同情況下的分類，如時鐘信號的抖動分類，數據信號的抖動分類以及這兩類抖動之間的聯系，指出了實際抖動測試過程中的注意事項，對抖動分析測試有一定的參考意義。

　　【關鍵詞】

　　峰峰值抖動 相位抖動 周期抖動固有抖動隨機抖動

　　一、峰峰值抖動、均方根抖動

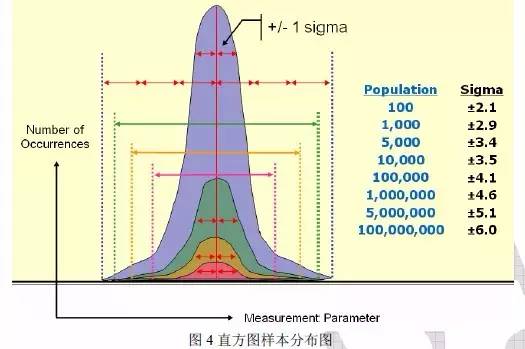
　　過去多年來用于量化抖動的最常用的方法是峰峰值抖動（Peak-to-peak Jitter）和均方根抖動（Root-Mean-Square Jitter，抖動直方圖或者抖動分布的1 或者RMS值）。但是由于隨機抖動以及非固定抖動的存在，使得抖動的峰峰值隨著觀察樣本數量的增加而增加，因此說峰峰值抖動參數用于衡量固有抖動會很有效，但是衡量隨機性抖動卻會出現很大誤差；相同的道理，由于固有抖動及非高斯性抖動和噪聲的存在，使得抖動的直方圖或者分布圖不呈現完全的高斯分布，因此統計得到的抖動的1σ或者RMS值不等于真實高斯分布的1 值。

　　峰峰值抖動和均方根抖動均是對某一類抖動的統計分析指標。

　　二、相位抖動、周期抖動、相鄰周期間抖動

　　由于時鐘系統是數字電路系統非常關鍵的一部分，直接決定了數據信號發送和接收的成敗，是整個系統的主動脈，因此時鐘的抖動一直備受關注。描述時鐘系統的抖動參量一般分為三類，即相位抖動（Phase jitter）、周期抖動（Period jitter）、相鄰周期間抖動（Cycle to cycle jitter）。

　　1、相位抖動

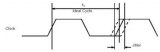
　　在數字系統中，兩個邏輯電平之間的切換通常伴隨著快沿的出現，這些邊沿在時序上的不穩定性就叫做相位抖動（phase jitter，有時也叫累積抖動，accumulated jitter，指實際邊沿位置與理想邊沿位置的偏差，以時間為單位，也可以換算成弧度，角度等）；相位抖動是相位噪聲在數字域的等效體現，它是離散量，因此只有當邊沿存在時候才有定義。

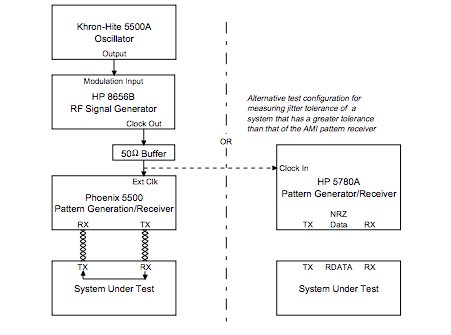
　　理想邊沿位置一般定義在數字信號一個比特位時間間隔的整數倍位置處。如下圖1所示為某一

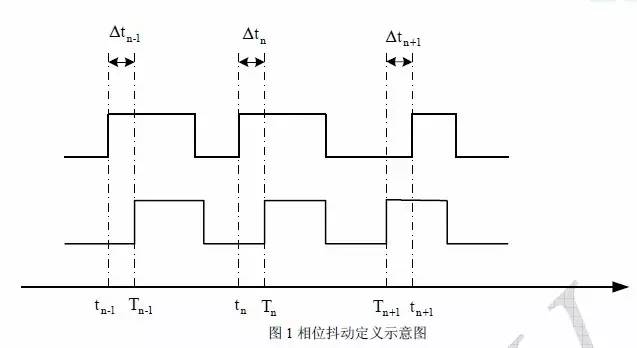
　　不會直接使用時鐘的邊沿來保證時序關系，而是看周期的穩定性，也就是周期的抖動，有時候時鐘周期越長，可能帶來保持時間余量不足的問題，這個時候就需要測量周期抖動；而相鄰周期間抖動常常可以用來衡量時鐘分頻器的穩定性。總之，這三種抖動都是衡量時鐘本身性能的指標，在不同的應用背景下需要關注不同的指標，通常時鐘芯片的手冊會給出對時鐘的抖動指標要求。

　　三、串行數據系統中抖動的分類

　　在上一篇文章中，我們提到了串行數據系統中接收端芯片的工作原理以及TIE（Time Interval Error）抖動的概念，即數據與時鐘之間的相對抖動，而不是單純指數據本身或者時鐘本身的抖動。那么如果我們假定時鐘邊沿位置（對于高速數據鏈路系統，或者叫異步系統來說，該時鐘一般是恢復時鐘）為數據的理想邊沿，那么數據的TIE抖動事實上就是前文中分析時鐘抖動時的相位抖動，唯一不同的是時鐘信號的相位抖動在每一個時鐘周期都會有一個數值；而數據信號常常有很多個連零電平或者連1電平，無邊沿存在，因此也就沒有對應的相位抖動數值。所以為了分清這兩類抖動的概念，我們姑且在本文中暫定義時鐘信號的相位抖動叫相位抖動；數據信號的相位抖動就叫做TIE抖動（時間間隔誤差）；

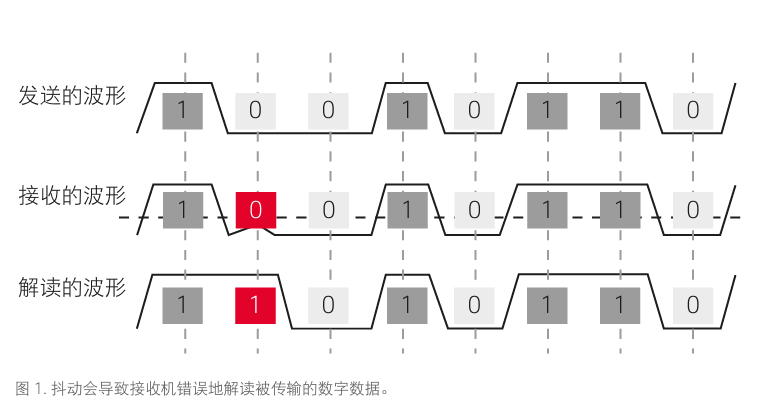
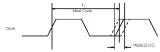
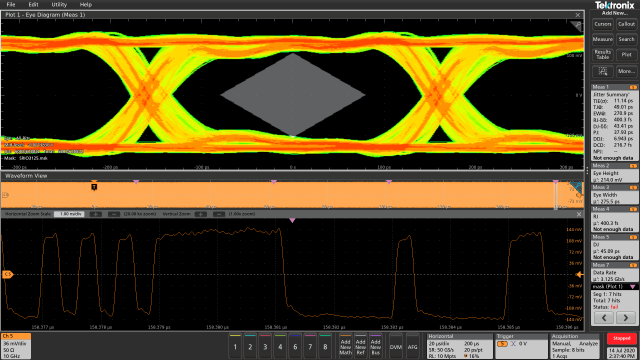
　　TIE抖動是分析串行數據抖動的最基本單位，數據信號的每一個邊沿位置都會有一個TIE抖動值。一段很長的串行數據一定會包含數個上升沿或者下降沿，如下圖所示：

　　如果將所有邊沿處的TIE抖動做一個直方圖統計，我們可能會發現這些TIE值是具有一定的統計規律的，如下圖所示分別為呈現高斯分布的TIE抖動以及呈現雙峰分布的TIE抖動：

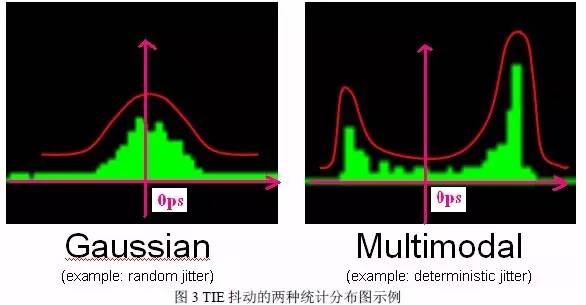
　　呈現高斯分布的抖動通常是由于熱噪聲等引起的，稱為隨機抖動（Random Jitter）；呈現雙峰且將高斯曲線分成兩部分的雙峰之間的抖動值稱為固有抖動（Deterministic Jitter）;通常來說抖動成分主要是由隨機抖動Rj和固有抖動Dj構成的，在之前的第二節我們有介紹到由于Rj的峰峰值是

　　****的，隨著累積樣本數的增加而增加，因此通常是用統計標準偏差值（幾個sigma范圍內的抖動值）來衡量的；而Dj則是用峰峰值來衡量的。當前大部分串行數據標準要求測量誤碼率為10e-12時的總體抖動（Tj）大小，而通常直方圖+/-7 sigma以內的數據樣本數才能達到10e+12。Tj就是衡量Dj與Rj的整體影響的抖動術語。誤碼率為10e-12時的總體抖動Tj=14Rj+Dj （Rj是指1sigma時的抖動或者叫RMS抖動；Dj是固有抖動的峰峰值）

　　如果我們不用統計的方式來分析TIE抖動，而是在一個很長的時間軸上來看所有的TIE抖動值的變化趨勢，即用如Lecroy示波器中的參數track的功能，我們也同樣能夠看出TIE抖動值的變化趨勢：

　　當TIE的樣本積累很多時，我們也能夠觀察到TIE參數變化的趨勢，如下圖所示，

　　上圖藍色波形即為TIE抖動參數的變化趨勢，呈現了周期性的變化，如果對其做FFT變換，會發現有周期性的頻譜成分，這類抖動就稱為周期性抖動（Pj），如下圖所示

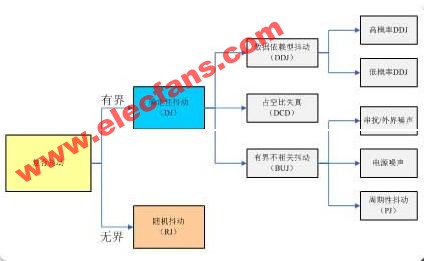
　　周期性抖動Pj為固有抖動Dj的一部分，除此以外，還有和數據碼型相關的抖動DDj（數據相關性抖動）；占空比失真引起的DCD抖動；因數據碼型中0電平和1電平切換頻率不同導致的碼間干擾抖動ISI（因為不同頻率的信號經過信道時衰減延遲是不一樣的）;由于高次諧波以及串擾引起的抖動，一般稱為OBUJ（其它的固有不相干抖動），這類抖動屬于固有抖動成分，但是數值很小，很容易和隨機抖動Rj混到一起，不易區分，Lecroy的NQ-SCALE方法能夠較好的區分出這類抖動。

　　綜上所述，串行數據的總體抖動Tj的構成如下樹狀圖：

　　四、時鐘抖動與數據抖動的聯系

　　主要有如下幾點：

　　1、數據抖動是以TIE抖動作為基本單位展開分析的，根據抖動的構成成分，將一定誤碼率情況下（特定的樣本數量）的總體抖動Tj分解為Dj，Rj，DDj，Pj等；因為數據信號不具備如時鐘信號一樣的周期重復性，因此數據信號沒有周期抖動、相鄰周期間抖動的指標。

　　2、高速串行數據標準一般要求在特定誤碼率情況下（如10e-12）的總體抖動Tj，固有抖動Dj，隨機抖動Rj等指標不能過大；而時鐘信號一般是芯片手冊給出要求，因此分析時鐘抖動時需要多大的數據量則需要引起注意，不一樣的樣本數據量，測得的抖動結果也會偏差很大。如果時鐘手冊給出的指標非常苛刻，則有可能是在1sigma范圍內的數據量進行測量分析的（數據量小，所以抖動也會小很多），參照圖4。

　　3、時鐘的相位抖動、周期抖動、相鄰周期間抖動也同樣可以作為基本單位進行統計分析，同樣也可以設定特定樣本數據時的Tj，Dj，Rj以及相關的分解（數據相關性抖動ISI等不適用于時鐘抖動，因為時鐘抖動0電平和1電平的切換率是恒定的），以便分析抖動的來源，但是如果用數據抖動的分析軟件來分析時鐘抖動的話一般只能分析相位抖動，周期抖動和相鄰周期間抖動只能通過直方圖以及參數跟蹤的方法來分析。

　　4、時鐘芯片手冊或者其它芯片手冊中給出的時鐘抖動指標通常是某一類抖動的峰峰值或者RMS值，也有要求總體抖動Tj，Dj，Rj指標的，給出這樣的指標時我們一定得搞清楚這個指標是對應于多大的樣本數據量。

　　編輯：黃飛