濾波器設計的逼近方法 - Butterworth, Chebyshev, Elliptic
引言
在學習濾波器設計時,書本上往往直接甩出濾波器的傳遞函數公式,讓人摸不著頭腦,到底這些傳遞函數公式是如何得來的呢?一般文章中也絕口不提其原理是什么,難道這背后是否有什么玄機,是不是隱藏著什么神秘的東西!
帶著疑問梳理了巴特沃斯(Butterworth)、切比雪夫(Chebyshev)、橢圓函數(Elliptic Function, Cauer)濾波器,終于對濾波器綜合和設計內容有了比較系統的理解。如果大家有興趣對這部分內容感興趣可以閱讀《威廉·卡爾(Wilhelm Cauer)的生活和工作》這篇文章,其中卡爾的網絡綜合綱領列出了濾波器綜合的3個問題,即
- 1, 可實現性(realizability)
- 2, 近似(approximation)
- 3, 實現與等價(realization and equivalence)
實際上這三個問題中第一個可實現性問題在當時已經被解決了,即 正實函數(Positive-real function, PR, PRF) 可以被無源電路實現,隨著時代發展,這部分內容已經被歸入到信號與系統中。
現在濾波器設計類書籍中討論最多的是第三個問題,即實現與等價,比如隨著計算機發展,我們還是沿著模擬濾波器的設計思路在設計數字濾波器,并且在不同平臺中實現,如何讓資源最小,速度最快等等方向發展;另外往高頻方向發展就引出了微波射頻濾波器,如微帶濾波器,腔體濾波器等等。現在工程中濾波器設計也主要集中在這一方面;有源器件發展的進步也豐富了濾波器設計。
現在關注最少的就是沒有被提及的第二個問題,即近似(逼近,Approximation),濾波器近似可以說不是工程師的強項,因為這涉及到太多太復雜的數學知識,從濾波器名字可以看出,這里用到了多少數學知識:
| 濾波器類型 | 相關人物 | 國籍 | 頭銜 |
|---|---|---|---|
| 巴特沃斯濾波器 | 巴特沃斯 | 英國 | 物理學家 |
| 切比雪夫濾波器 | 切比雪夫 | 俄羅斯 | 數學家 |
| 橢圓函數濾波器 | 雅可比 | 德國 | 數學家 |
| 卡爾 | 德國 | 數學家 | |
| 貝塞爾濾波器 | 貝塞爾 | 德國 | 數學家 |
| 勒讓德濾波器 | 勒讓德 | 法國 | 數學家 |
| 高斯濾波器 | 高斯 | 德國 | 數學家 |

可以看到一票的數學家,這方面發展現在主要集中在數學領域,比如逼近論就是數學的一個分支。
本文并不會嚴格的對數學公式進行推導,只是從工程師角度去直觀理解濾波器設計所用的逼近方法,讓人不再對濾波器設計存在盲區和疑惑。
另外下述討論的濾波器設計逼近方法都是針對低通濾波器而言。
下圖是對濾波器綜合設計流程的梳理:
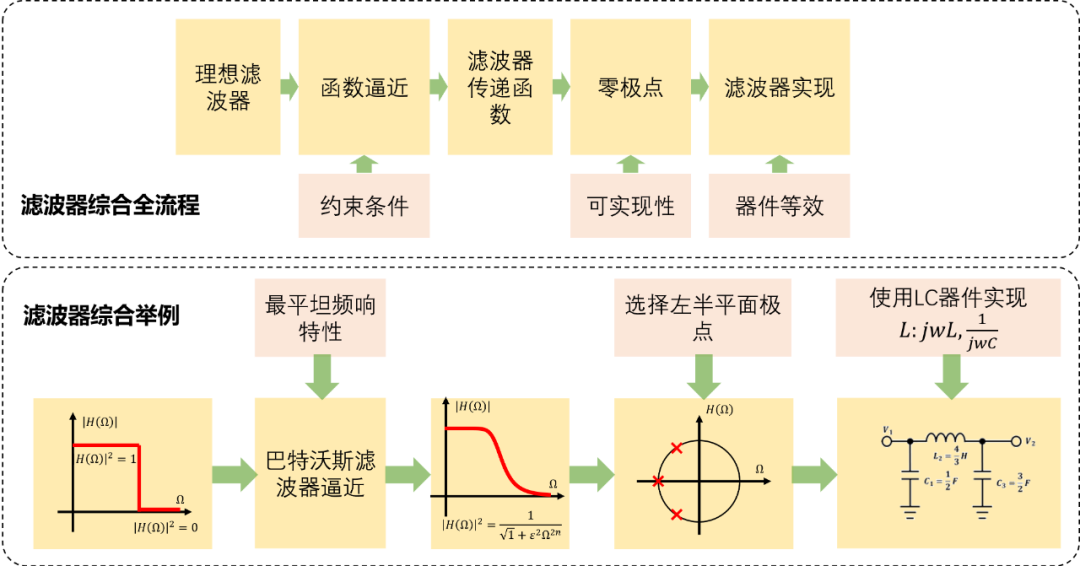
在濾波器逼近中最重要的是一步就是確定 約束條件 ,通俗一點講就是提指標。下述濾波器逼近中單獨將約束條件作為一個小結來說明。
特征函數(The Characteristic Function)
在電路中,歷史上濾波器傳遞函數定義是:
由電壓轉到功率:
再由功率反射,得到反射系數,即反射到信號源的功率和輸入總功率的比值:
聯立(1),(2)得到:
令,得到
這里的就是 特征函數 。
特征函數有個好處是它只關注濾波器形狀本身,并不關心濾波器的這個低頻分量1,從而簡化了計算,以下我們對濾波器函數的逼近最終都逼近到特征函數為止。
濾波器的衰減用如下公式計算,單位為dB:
現在濾波器設計中我們往往使用如下傳遞函數表示幅頻響應:
注意它的dB形式和衰減的dB形式函數圖像沿著橫坐標鏡像對稱。
巴特沃斯濾波器逼近
巴特沃斯濾波器是具有最平坦頻響特性的濾波器,如何理解這句話?在低通濾波器中,最平坦是指0頻率處有最平坦特性,假設特征多項式為,其中為截止頻率處的最大衰減量。
約束
由前面可知要實現一個可以綜合的網絡,首先我們要找到一個正實函數來逼近所需要的特性,要滿足0頻率處由最平坦特性,那么要求其:
- 1, 是一個階多項式(可實現性)
- 2, (低通定義,在頻率為0的位置無衰減)
- 3, (低通定義,截止頻率在1)
- 4, 在0頻率處各階導數為0(在最低頻率處具有最平坦特性)
函數逼近
由以上約束條件1,我們定義多項式為:
由約束條件2,得到:
由約束條件4,我們求其1階導數:
并且讓等于0,得到:
同理我們讓其2階導數為0,得到:
一直到第階導數為0,得到:
這時不能再求導,因為再求導就會使得,那么就不是一個階多項式了。 到這里特征多項式變為:
由約束條件3,得到:
最終得到巴特沃斯濾波器特征函數:
將巴特沃斯濾波器的幅頻響應函數重寫如下:
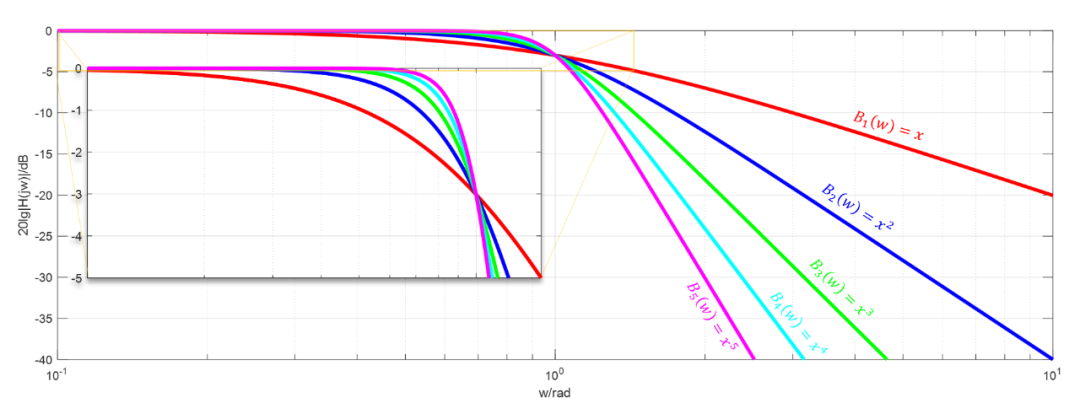
擴展
若我們想要得到處具有最平坦響應的低通濾波器,那么特征函數應該是什么樣呢?
照例還是寫下約束條件:
- 1, 是一個階多項式(可實現性)
- 2, (低通定義,在頻率為0的位置無衰減)
- 3, (低通定義,截止頻率在1)
- 4, 在1/2頻率處各階導數為0(在最低頻率處具有最平坦特性)
m階導數等于0,且,且,得到個方程的方程組:
設,則有
解得:,最終得多項式為:
設,則有
解得:
最終得多項式為:
繪制5階和7階頻響曲線如下:
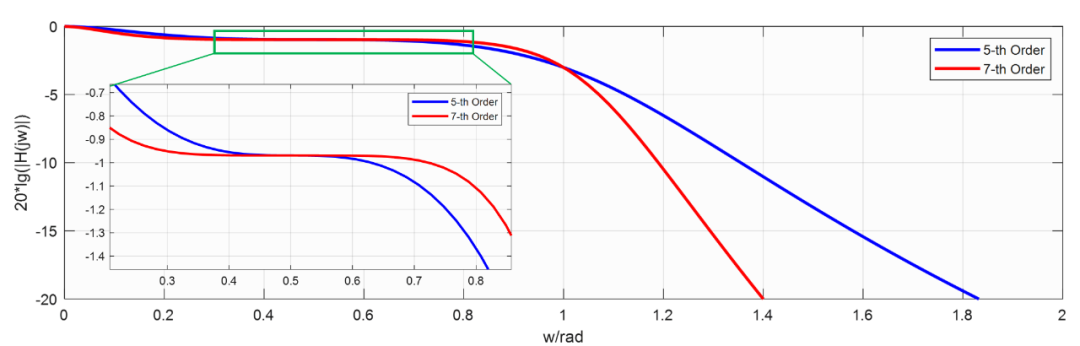
從頻響曲線可以看出,在處有最大平坦特性,在這里我們綜合出了一種特殊的濾波器!
比較這種B0p5(暫且叫做這個B0p5)濾波器和傳統的巴特沃斯濾波器特性,有圖有真相(圖中比較位置將巴特沃斯濾波器頻響往下移動并和B0p5重合,方便比較):
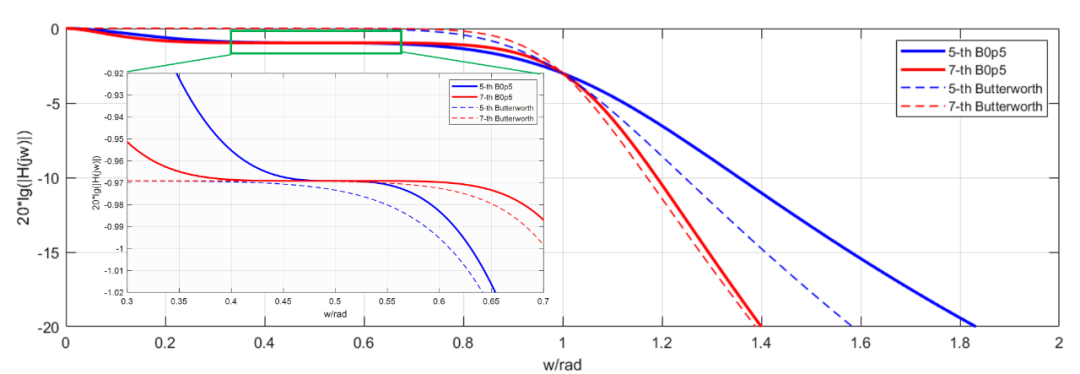
結果顯示對于高階,B0p5和普通巴特沃斯在高頻抑制方面基本沒有太大區別,區別在于快接近截止頻率處B0p5要更為平坦,但是其代價就是犧牲了插損,差不多有1dB!有得必有失。
切比雪夫濾波器逼近
實際應用巴特沃斯濾波器的過程中,有沒有發現一個問題,即巴特沃斯濾波器在截止頻率附近的衰減都比較大,比如要濾除一個點頻測試源的3次諧波,那么截止頻率設計值要比實際有用信號頻率值要高很多才不至于將我們關心的基波頻率衰減很多。這也從側面反應了巴特沃斯濾波器的一個缺點是為了保證0頻率附近的平坦性,犧牲了其他頻率的插損。尤其頻率越高插損越大。
所以為了解決這個問題,人們改變了濾波器綜合思路,不再去強調某一個點的特性,我們關注一個頻段的特性,這也就是我們將要介紹的切比雪夫濾波器綜合所要討論的內容。
切比雪夫濾波器特性是通帶范圍內具有等紋波特性。假設特征多項式為,其中為通帶紋波。
約束
由前面可知要實現一個可以綜合的網絡,首先我們要找到一個正實函數來逼近所需要的特性,要滿足在通帶內具有等紋波特性,那么要求其:
- 1, 是一個階多項式(可實現性)
- 2, (低通定義,截止頻率在1)
- 3, 在通帶內擺動幅度在內(通帶內等紋波特性)
- 4, 是奇函數如果為奇數; 是偶函數如果為偶數(可實現性,方便實現)
函數逼近
這里為了簡單起見,只對進行討論,其他階數的任意階濾波器都可以用類似的方法去推導。 首先我們由約束2,3和4繪出階濾波器的的大致函數圖像(階函數具有個過0點):
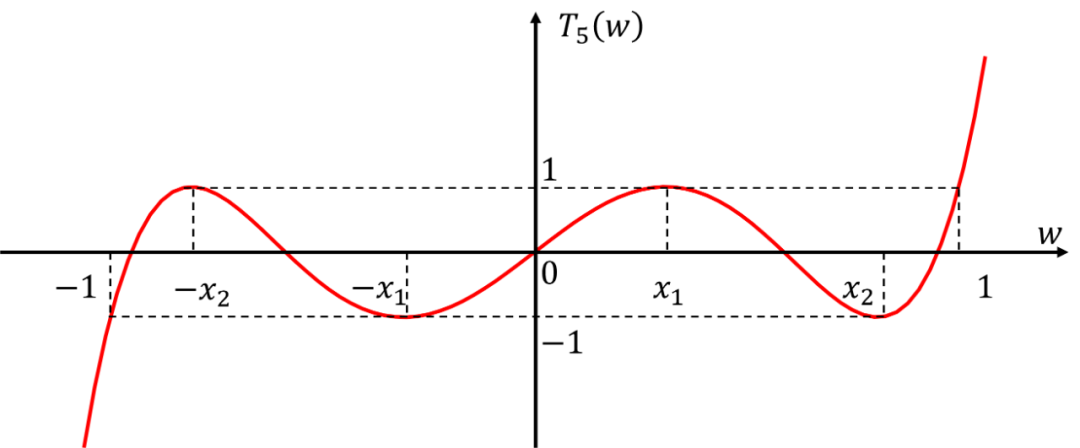
由約束1,令特征多項式為一個5次多項式:
若對這個方程求導,則得到一個4次方程,這個方程有4個根,由上述曲線極值點位置,可以得到這4個根,則列出第一個方程:
為了再和這些根扯上關系,繪出的函數圖像
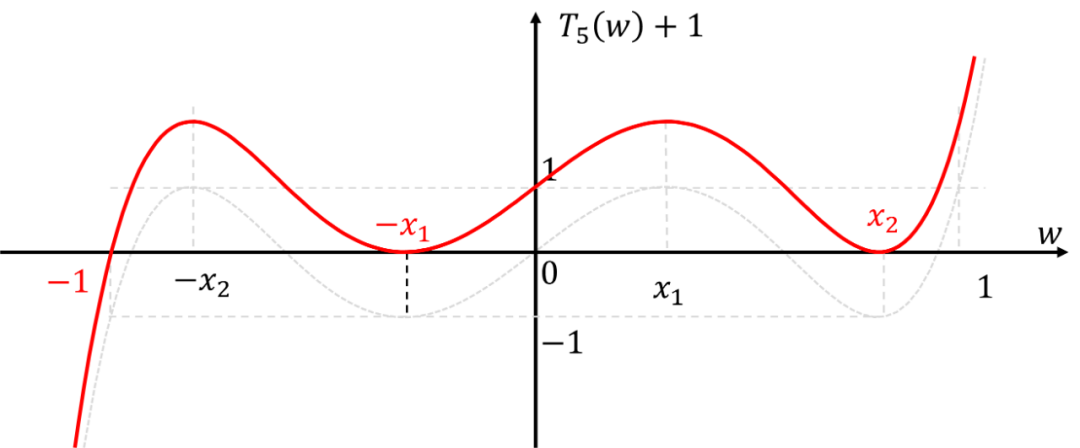
那么依據過0點位置,我們又可以得到一組方程:
這里要注意,由于曲線在拐彎的位置是有兩個重根的,上式驗算下方程的方次也可以推算出來。 同理,我們繪出的函數圖像
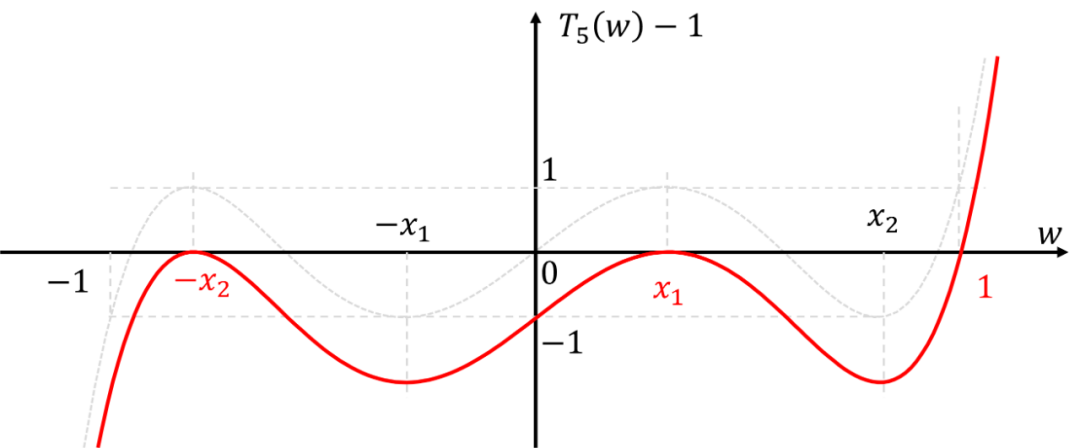
那么依據過0點位置,我們還可以得到一組方程:
將(8)和(9)左右相乘得到:
將(7)和(10)聯立得到:
式(11)變形如下:
上式微分方程可以通過兩邊積分,得到:
于是得到時眾所周知的切比雪夫函數:
對于其他階數的切比雪夫濾波器,可以用同樣的辦法,最終得到階切比雪夫函數為:
另外,對于這個公式比較嚴謹的推導見譯文《切比雪夫逼近方法》。
擴展
假設我們不關心低通濾波器的低頻第一個紋波,而是讓低頻到之間在之間等紋波,低頻之間有最大值,那么應該如何進行函數逼近呢? 照例列出約束條件:
- 1, 是一個階多項式(可實現性)
- 2, (低通定義,截止頻率在1)
- 3, 在通帶內擺動幅度在內(規定的通帶內等紋波特性)
- 4, 是奇函數如果為奇數; 是偶函數如果為偶數(可實現性,方便實現)
PS. 這里暫時討論偶數階情況,具體的;奇數階情況非常復雜,留著以后討論。
則特征多項式為:
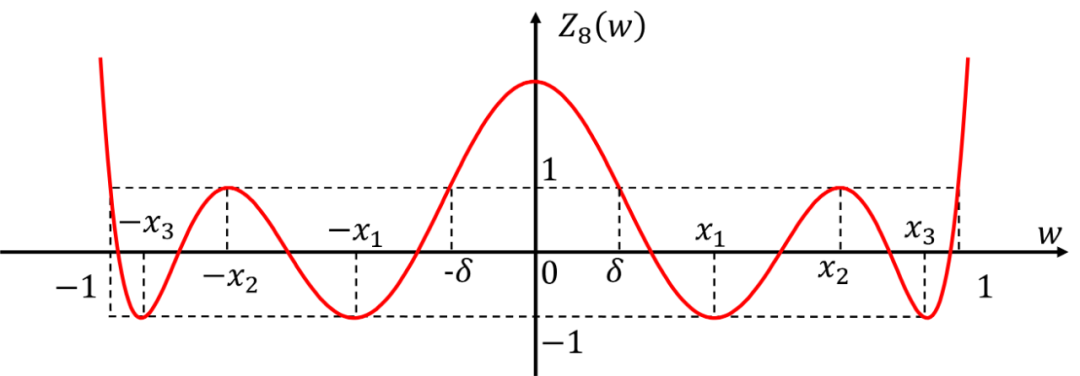
同樣的對其進行求導得到:
然后計算,得到:
然后計算,得到:
同樣將上式左右兩邊相乘:
將微分方程代入上式:
整理得到:
其中
所以最終結果為:
不同下繪圖:
!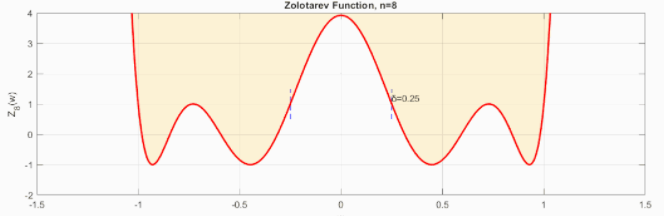
實際上這種濾波器名叫Achieser–Zolotarev濾波器或Zolotarev濾波器,在數字濾波器和微波濾波器中有應用。
橢圓函數濾波器逼近
由[模擬無源濾波器設計(六)-Chebyshev濾波器設計詳解]可知逆切比雪夫濾波器"具有最平坦的通帶頻率響應,阻帶具有等紋波特性",而同樣具有最平坦通帶響應的巴特沃斯濾波器,同樣的階數,那么為什么逆切比雪夫濾波器過渡帶如此陡峭呢,究其原因就是因為逆切比雪夫濾波器的零點不在無窮遠,它以犧牲無窮遠處的衰減為代價換來了陡峭的過渡帶。
那么沿著同樣的思路,對于切比雪夫濾波器具有的無窮遠處的極點,我們是否也可以將其移動到有限位置,從而讓過渡帶更加陡峭呢,答案是肯定的,這就是這一節所介紹的橢圓函數濾波器。
橢圓函數濾波器是通帶和阻帶都具有等紋波特性的濾波器。假設特征多項式為,其中為通帶紋波。
約束
由前面可知要實現一個可以綜合的網絡,首先我們要找到一個正實函數來逼近所需要的特性,要滿足在通帶和阻帶內都具有等紋波特性,那么要求其:
- 1, 是階的兩個有理數多項式之比(可實現性)
- 2, (自逆性,方便實現)
- 3, 是奇函數如果為奇數; 是偶函數如果為偶數(可實現性)
- 4, 的所有個零點都在頻帶內,所有個極點都在帶外(等紋波特性)
- 5, 在通帶范圍擺動幅度在內(通帶內等紋波特性)
- 6, (低通定義,截止頻率在1)
- 7, 在阻帶范圍擺動幅度在內,其中和都在范圍內(阻帶內等紋波特性)
函數逼近
對于為偶數,由約束1, 2, 3, 4可得,有如下形式的多項式結構:
這種結構特點是零極點相互關系固定,當確定了零點位置那么極點位置也就確定了,并且通帶和阻帶零極點關于對稱。
為簡便直觀起見,這里對進行函數逼近。
繪出得草圖,得到:
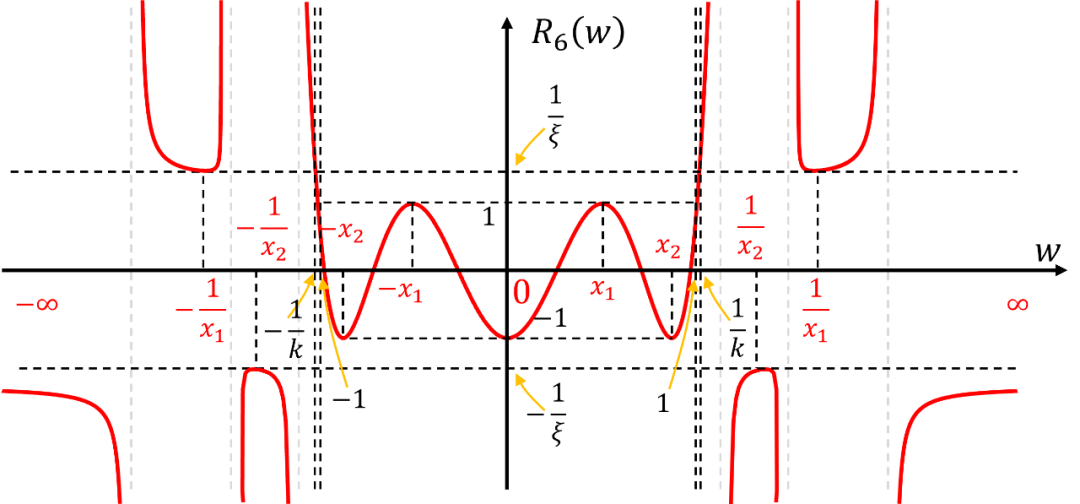
和之前切比雪夫逼近類似,首先建立微分關系,從圖中可以觀察到對于階的函數,其通帶內極值點在值為1處有個(圖中的和),在通帶內值為-1處的極值點有個(圖中的, 和);在阻帶值為處有個(圖中的和),在阻帶值為處有個(圖中的, 和),在阻帶的極值點可以通過約束4來推導,個數同通帶內極值點。圖中所有極值點都用紅色字符標注,注意無窮只算一個極值點。對于階函數,總的極值點有個。函數求導并平方后的極值點個數為。
所有極值點都位于函數值等于和處,另外再除掉頻率為和的4個點(圖中的和)。
所以最終函數求導后再平方結果如下:
上式為常數,化簡得到:
整理得到:
令,再次整理得到最終標準微分方程:
對上式兩邊積分,得到第一類橢圓積分標準形式,具體求解過程見《濾波器設計中的橢圓函數講解》,最終得到濾波器特征方程為:
是雅克比橢圓函數,類比于三角余弦函數,可以看到其方程形式和切比雪夫濾波器特征方程(15)一樣。
濾波器頻率響應:
式中, , 繪圖得到:
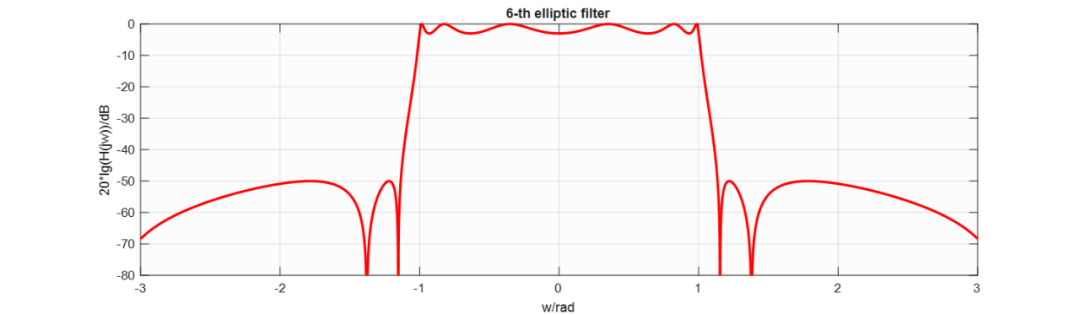
對于其他階橢圓函數濾波器,令并且,其特征函數標準微分方程為:
上式是一個中間變量,便于分析和后續處理,最終特征函數為:
總結
本章節對巴特沃斯(Butterworth)、切比雪夫(Chebyshev)、橢圓函數(Elliptic Function/Cauer)濾波器綜合中的逼近方法進行了講解,并且做了一些拋磚引玉式的擴展,總體來說函數逼近論比較復雜,比如對切比雪夫濾波器得擴展就在奇數階設計綜合中遇到了困難,這里涉及到比較多的雅可比橢圓函數的知識。后續的其他濾波器綜合類文章,都是按照濾波器綜合流程來行文,這樣更加系統和連貫。
 電子發燒友App
電子發燒友App











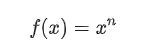










評論