作為模擬工程師,環路穩定性是一個繞不開的話題,很多運算放大器的書籍也或多或少對運算放大器的穩定性都有介紹,但看下來都不夠完整,或者部分知識點有些陳舊,基于此,搬運工重新梳理并整理成本文運算放大器的穩定性。本文比較長,為了更有目的性的閱讀,大家可以帶著以下幾個問題點去詳細閱讀本文,并在閱讀完之后再回頭來看看這些問題是否都得到了很好的答案。
1. 運算放大器的開環增益、環路增益、閉環增益的區別?
2. 運算放大器環路不穩定的判定條件以及原因?
3. 運算放大器環路穩定性的判定依據?
4. 什么是相位裕度和增益裕度?
5. 如何理解波特圖中的幅度改變率、相位改變率、極點、零點?
5. 如何理解運算放大器規格書中Gain/Phase頻率曲線中Phase有正有負?
6. 如何根據規格書中開環Gain/Phase頻率曲線快速判定環路穩定性?
7. 如何理解相位頻率曲線的非單調性以及其對群延時的影響?
8. 如何理解環路增益AOLβ中開環增益AOL和反饋系數β隨頻率變化的特性?
一、運算放大器的負反饋
負反饋電路在運算放大器的應用中起著非常重要的作用,它可以改善運放的許多特性,比如穩定增益,減小失真,擴展頻帶,阻抗變換等。但負反饋的引入也有可能會使得運算放大器電路不穩定,輕則帶來時域上的過沖,重則會引起自激振蕩。運算放大器的自激震蕩
二、運算放大器的穩定性
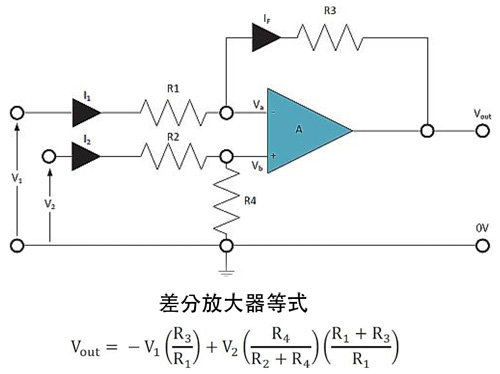
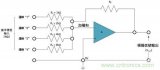
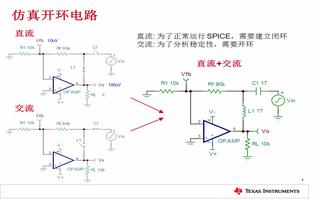
為了簡化分析,下面以同相放大器為例,來從零開始解析運算放大器的穩定性,如下圖所示,是同相放大器的環路系統框圖以及對于同相比例放大器的實際電路示意(標注出對應的反饋系數-β網絡)。
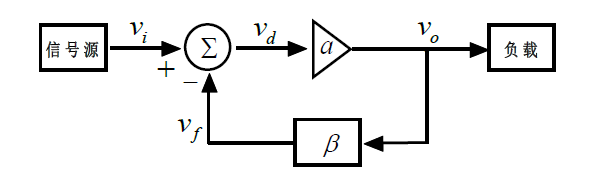
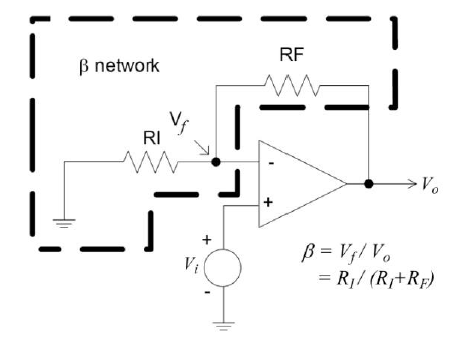
從上圖反饋環路系統框圖中,得知對于一個負反饋電路,主要包含:
增益模塊:增益為a,接受輸入差分信號vd,輸出vo,即vo=a×vd,這里對于同相比例放大電路,其增益模塊即是運算放大器本身,a則是其開環增益AOL。
反饋網絡:反饋信號網絡,vf=β×vo,β則是該反饋網絡的增益,也是常說的反饋系數。
疊加模塊:vd=vi-vf,這里可以看到所謂負反饋,是在輸入信號源上減去反饋的信號后得到差分信號,如果是vd=vi+vf,則是正反饋系統。 基于以上的簡單推導,可以得到同相比例放大電路的閉環增益(Acl)表達式如下:
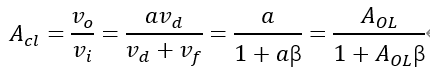
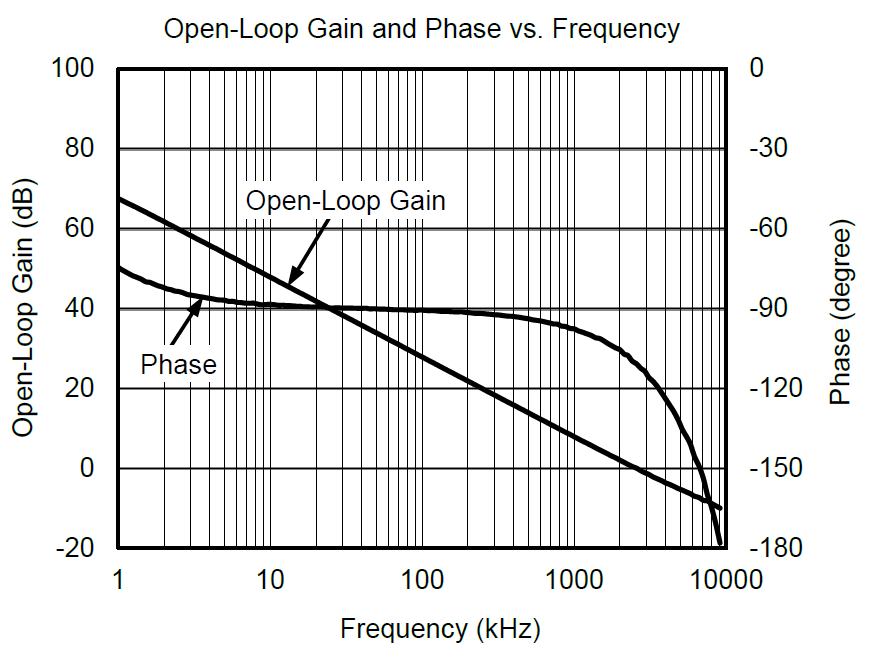
AOLβ,這是一個非常重要的表達式,稱之為環路增益,從上述閉環增益的表達式可以看出,一個負反饋系統的穩定性程度主要取決于其環路增益AOLβ,這里β對于同相比例放大電路,因為反饋網絡只有電阻元件,其值跟頻率沒有關系,β=vf/vo=RI/(RF+RI),而AOL則是一個隨頻率變化的曲線(如上圖OPA規格書中給出的開環增益和相位與頻率的曲線圖,其幅度和相角都會隨頻率變化而變化 ),所以從數學上理解,AOL是一個復數,會對應有幅度和相角度,所以這里對于環路增益AOLβ又可以表達成如下形式(其中f是代表頻率,θ代表相角):
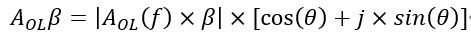
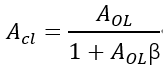
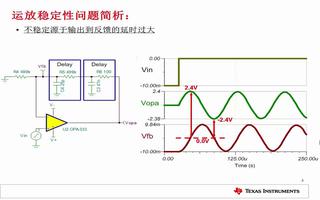
所以當AOLβ=-1的時候,1+AOLβ為無窮大,閉環增益趨于無窮大,這個時候輸入端任何輕微的擾動都會在輸出引起劇烈的反應,此時負反饋系統變成了正反饋,進而導致運算放大器的自激震蕩的產生。從AOLβ的復數表達式來看(這里是以往所有講運算放大器穩定性都沒有提到的一個概念),對于|AOLβ|=1,當θ=-180°時,cos(θ)=-1,sin(θ)=0,則有AOLβ=-1,所以對于不穩定的條件是|AOLβ|=1以及θ=-180°。所以判定穩定性時,需要保證遠離以上兩個進入不穩定的條件,下面分開從這兩個不穩定條件來看:
1. 當AOLβ的相角θ=-180°時(信號過系統之后的相移為-180°,負反饋變成正反饋):|AOLβ|<1:0<1+ AOLβ<1,正反饋信號逐漸衰減,會產生過沖但不會震蕩。|AOLβ|≥1:AOLβ=-|AOLβ|≤-1,即1+ AOLβ≤0,如果1+ AOLβ<0,則Acl<0,但因為運算放大器本身的限制,對于同相比例放大無法產生負的閉環增益,從而最終只能工作在1+ AOLβ=0的狀態,導致運算放大器工作在不穩定條件下而發生震蕩。因此在|AOLβ|≥1的任何時候都需要避免反饋環路的相移達到或超過180°。
2. 當|AOLβ|=1時:θ<-180°,這里主要看相位余量的大小,會有過沖,但不會震蕩,通常所說的相位裕度,就是指在|AOLβ|=1(環路增益20lg(1)=0dB)時候的相移距離-180°差值,一般AOLβ至少有45°的相位余量才能讓負反饋系統足夠穩定。θ≥-180°,會震蕩。這里先不展開分析,為了更形象的說明上面兩個判定環路穩定性的依據,我們有必要先引入一個分析環路穩定性的必備工具,波特圖。
三、環路穩定性少不了的工具-波特圖
這里先簡單回顧下波特圖的幾個基本概念:
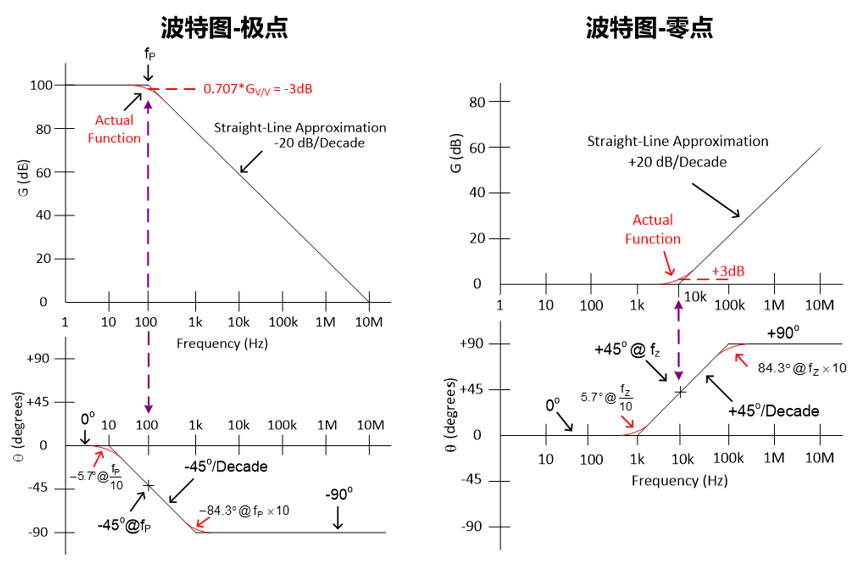
1. 幅度改變率(Roll off Rate):幅度曲線中幅度改變的速率,一般用 dB/decade為單位。為正(+)值時表示上升,為負(一)時表示下降。
2. 相位改變率:相位曲線中相位改變的速率,一般用°/decade 為單位。為正(+)值時表示上升,為負(一)時表示下降。
3. Decade: 十倍頻,頻率按 ×10 的速度增加,如 10KHz 到 100KHz 為一個 Decade。常與其他單位配合用來表示某個量在 10 倍頻程中改變的大小。
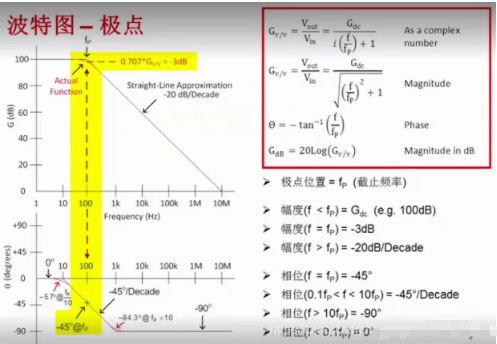
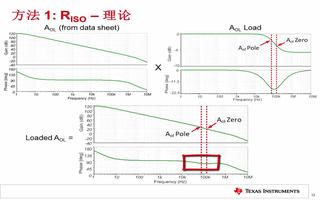
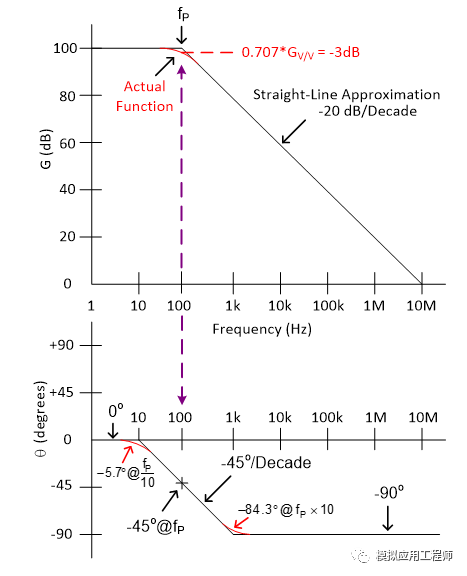
4. 極點:傳遞函數分母上的轉折點稱為極點。以上圖為例,單個極點響應在波特圖(幅度或增益曲線)上具有按 一20dB/decade 斜率下降的特點。與圖中的理想曲線不一樣的是,在現實中,極點位置在增益等干直流增益減去 3dB 的地方,該外對應的頻率即為轉折頻率。在相位曲線上,極點在轉折頻率上具有-45°的相移。相位在轉折頻率的兩邊以-45°/decade 的斜率變化為 0°和-90°。請注意極點是如何影響直到高于和低于極點頻率 10倍頻程處的相移的。單極點電路可以用簡單的 RC 低通濾波器表示。
5. 零點:和極點對應,傳遞函數分子上的轉折點稱為零點。以上圖右圖為例,單個零點響應在波特圖(幅度或增益曲線)上具有按 +20dB/decade斜率上升的特點。與圖中的理想曲線不一樣的是,在現實中,零點位置在增益等于直流增益加上3dB的地方,該處對應的頻率即為轉折頻率。在相位曲線上,極點在轉折頻率上具有-45°的相移,相位在轉折頻率的兩邊以 +45°/decade 的斜率變化為 0°和 +90°。請注意零點是如何影響直到高于和低于零點頻率 10 倍頻程處的相移的。單零點電路可以用簡單的 RC 高通濾波器表示。到這里為止,回顧了波特圖中的幾個重要概念,下面我們來看看如何用波特圖來幫助我們分析運算放大器的穩定性。
四、利用波特圖分析運算放大器環路穩定性
相位裕度定義:在運放開環增益和開環相移圖中,當運放的開環增益下降到1(0dB)時,開環相移值減去-180°得到的數值。
增益裕度定義:在運放開環增益和開環相移圖中,當運放的開環相移下降到-180°時,增益dB值取負,或者是增益值的倒數。
從相位裕度和增益裕度的定義(上述定義摘錄《你好,放大器》2.14),可以簡單的認為相位裕度和增益裕度越大,說明放大器越容易穩定,但顯然僅僅用相位裕度和增益裕度這兩個指標來判定環路穩定性是不夠的,上面我們有講過判定運算放大器環路穩定性的兩個依據(從工程經驗上來看,第二個判定依據實際應用中更好去衡量):
1. 當AOLβ的相角θ=-180°時|AOLβ|<1:會產生過沖但不會震蕩。|AOLβ|≥1:會震蕩。
2. 當|AOLβ|=1時:θ<-180°,會有過沖,但不會震蕩,相位余量45°以上環路更穩定。θ≥-180°,會震蕩。
可以看到,對于運算放大器的環路穩定性的判定,本質上都是對環路增益AOLβ的判定,所以嚴格來講,上述對相位裕度和增益裕度的定義并不準確,應該增加一個條件,即對于單位增益的時候,β=1,這個時候環路增益AOLβ就是運算放大器的開環增益。因為相位裕度和增益裕度是用來衡量運算放大器穩定性比較量化的指標,所以我們修正下這兩個定義如下:
相位裕度定義:在環路增益和相移頻率曲線中,當環路增益下降到1(0dB)時,相移值減去-180°得到的數值。
增益裕度定義:在環路增益和相移圖中,當環路相移下降到-180°時,增益dB值取負,或者是增益值的倒數。
基于此,我們來參考TI的OPA2991規格書中關于相位裕度(Phase Margin)這個指標的標注,可以看到,實際對于器件來說,相位裕度都是對于給定閉環增益(G=+1)條件下的一個指標,即β=1,AOLβ=AOL。

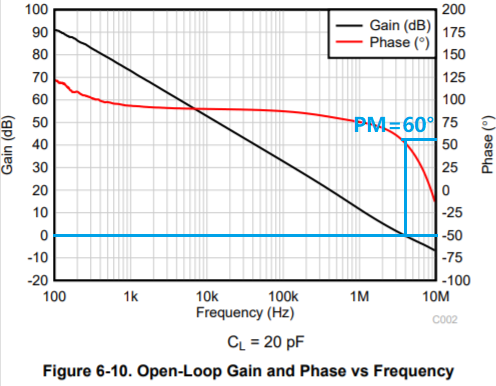
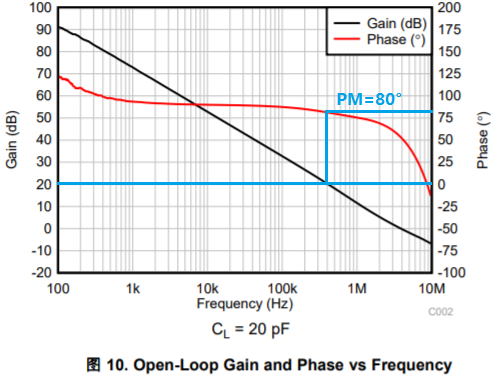
上圖是OPA2991規格書中Open-Loop Gain and Phase頻率響應曲線,基于這個曲線,對于G=+1(β=1)的時候,從圖中讀出在0dB處,其相位裕度為60°,可以判定OPA2991在單位增益(跟隨器)時環路是穩定的。
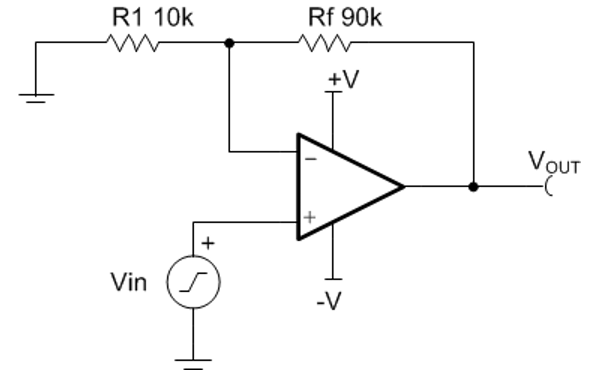
上面討論的都是單位增益,如下圖所示,是一個典型的同相10倍放大電路,該電路的反饋系數β=R1/(R1+Rf)=1/10,1/β=20log(10)=20dB。
對于環路增益AOLβ取對數計算,可以得到如下:
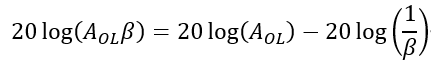
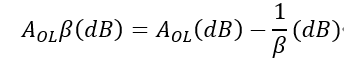
所以對于環路增益AOLβ=0dB處的相位裕度,即可以在OPA2991開環增益曲線上先畫出1/β(20dB)的線,然后AOL和1/β曲線交叉處即是環路增益AOLβ=0dB處,同時其對應的Phase就是AOLβ=0dB處的相位裕度80°(這里主要是因為對于純電阻的反饋網絡β是不會引起額外的相頻曲線的變化),所以對于OPA2991在G=+10的條件下,根據其環路增益的相位裕度為80°,判定環路穩定的。
五、環路穩定性分析中常見的幾個疑惑
1. 運算放大器規格書中開環增益曲線中的Phase有正有負。

?
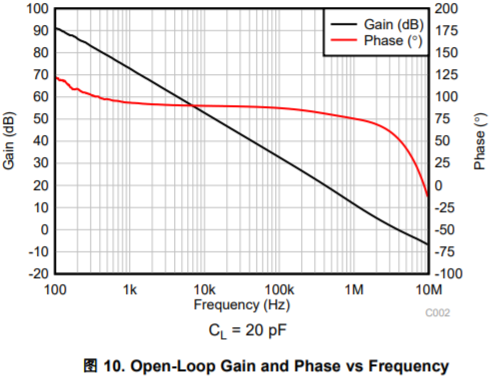
有細心的同學可能已經注意到,本文上述提到過的兩個開環增益/相位頻率曲線中Phase的數值不太一樣,上圖(左)的Phase都是負值,上圖(右)的Phase則是從正到負。這里我們要先明確一點,對于信號經過運算放大器,其相位肯定是滯后的,即相角是負的。
對于上圖(左)中標注的Phase就是我們正常理解的相移,對于這種圖示,其相位裕度是讀出來的Phase-(-180°)。
對于上圖(右)中標注的Phase,其實是Phase Margin,即Phase+180°的值。
2. 為什么有些運放規格書中相位頻率曲線不單調?不單調會帶來什么影響?一般運算放大器規格書中都會標注G=+1時候的相位裕度,通常對于單極點運算放大器來說,其相位隨頻率變化是單調的,單位增益處的相位裕度是最小的,只要保證了單位增益處的相位裕度滿足穩定性判定依據即可,上述提到的兩種開環增益/相位頻率曲線均符合。但這并不是絕對的,如下是國內運算放大器廠商思瑞浦TPA5562數據手冊中的開環增益/相位頻率曲線。
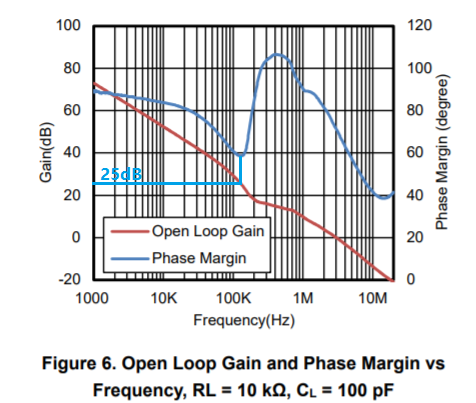
從上圖可以看到,TPA5562在單位增益(0dB)處的相位裕度是70°,但在25dB處的相位裕度是60°(25dB處的相位裕度比0dB處要小),其整個相位頻率曲線是非單調的,可以明顯看出,在120kHz頻率處,TPA5562內部做了零點補償,從而使得相位以+45°/decade的速率上升。單純的從環路穩定性來看,TPA5562在1/β>0dB以上的環路增益對應的相位裕度都可以滿足PM>60°,即保證了環路穩定性,但這種相頻曲線對實際應用會產生什么影響呢?這里引入群延時(Group Delay)的概念,輸出正弦波和輸入正弦波之間,會存在相移,也就相應的存在延時,當輸入波形為復合波形,包含多個不同頻率的正弦波,且它們的相移沒有特殊的規律,就可能出現不同的延時,這會引起輸出波形與輸入波形形態不同,造成線性失真。所以對于TPA5562這種相頻曲線,對于輸入信號是包含100kHz~400kHz之間的多個不同頻率正弦波的復合波形,則輸出雖然環路穩定,但會造成嚴重的線性失真。(本文主要講環路穩定性,這里簡單借助群延時的概念說明下這種相頻曲線的實際應用影響,后續可以單獨詳細討論群延時。)
3. 反饋系數β會隨頻率變化么?
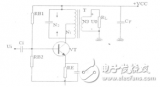
上面討論的都是基于反饋網絡是純電阻,即反饋系數β是不隨頻率變化的值,然后對于實際應用中很多時候反饋網絡包含了電容,對于包含電容的反饋網絡的反饋系數β的表達式就是一個隨頻率變化的函數。
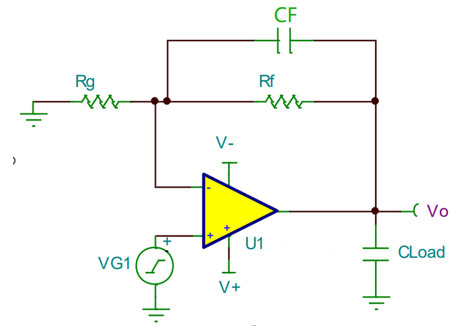
如上圖所示,是一個典型的在比例放大電路上增加了反饋電容的電路,這個時候其β的表達式如下,其是一個隨頻率變化的值,這個時候分析環路穩定性需要考慮1/β引入的額外的零極點(這部分后續會單獨寫文章討論關于同相比例放大電路的CF補償電容的計算)。
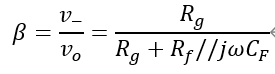
 電子發燒友App
電子發燒友App













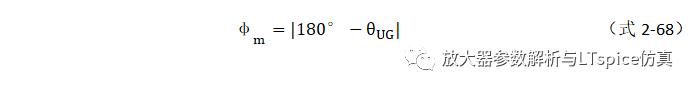










評論