友情提示,運放電路的噪聲分析還是比較復雜的,不論是基礎理論還是對應的推導過程,都不是特別容易。考慮到兄弟們的基礎參差不齊,所以我還是盡量說清楚點,這樣導致看起來就有點羅里吧嗦,也會看起來超級復雜,希望不會勸退。
1、關于噪聲我想過的幾個問題
我一般是帶著一些問題去學一些東西,找答案,個人感覺這樣主動式的要比被動式的理解更為透徹。說下我之前想過的一些問題吧,這些問題也會在后面得到解答。
問題1:白噪聲是隨機的,并且是全帶寬的,如果某個時刻,正好是各個頻率噪聲的波峰疊在一起,那噪聲電壓不是無窮大?概率雖然低,可能性是存在的吧,但是我們好像不會在電路設計中考慮這個問題。
問題2:一般運放手冊給出的噪聲參數有兩種,分別是電壓噪聲頻譜密度和電流噪聲頻譜密度,單位分別是伏特除以根號赫茲,和安培除以根號赫茲。這個是什么意思,如何轉化為我們常規理解的電壓信號呢?

問題3:運放的噪聲跟構成的電路增益有關嗎?會不會被放大?
問題4:對于一個具體的運算放大器放大電路,如何評估輸出端的電壓噪聲大小?
我們就帶著上面的問題來學習下。
2、噪聲參數與分析基本原理
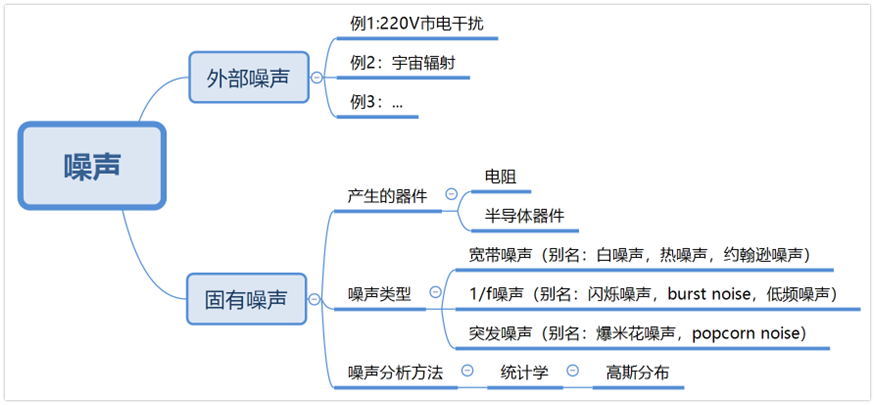
a、噪聲類型
噪聲可以分為兩類:外部噪聲和固有噪聲,我們本節主要評估運放的固有噪聲。
外部噪聲:外部電路或自然因素導致的噪聲,比如220V的市電干擾,宇宙輻射都是外部噪聲。外部噪聲很難估計。
固有噪聲:固有噪聲是由電路的元器件引起的,比如電阻和半導體器件都可以產生噪聲。固有噪聲可以估計。
b、噪聲波形特點
寬帶噪聲波形(高斯分布):
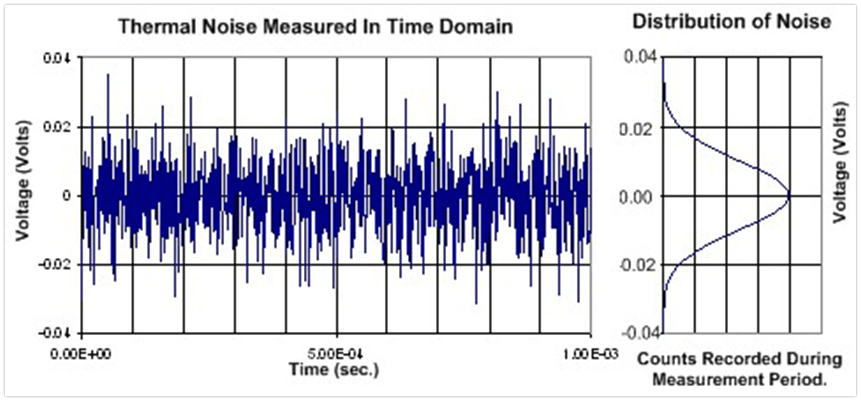
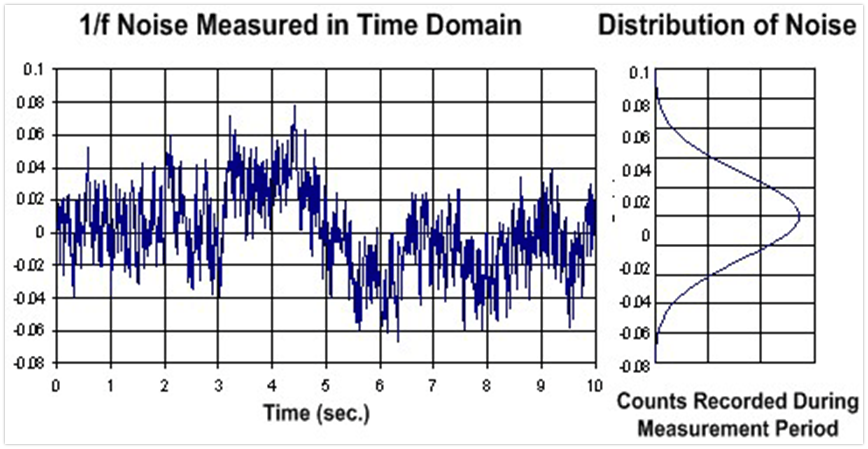
1/f噪聲波形(高斯分布):
爆米花噪聲波形(幾個高斯分布疊加):
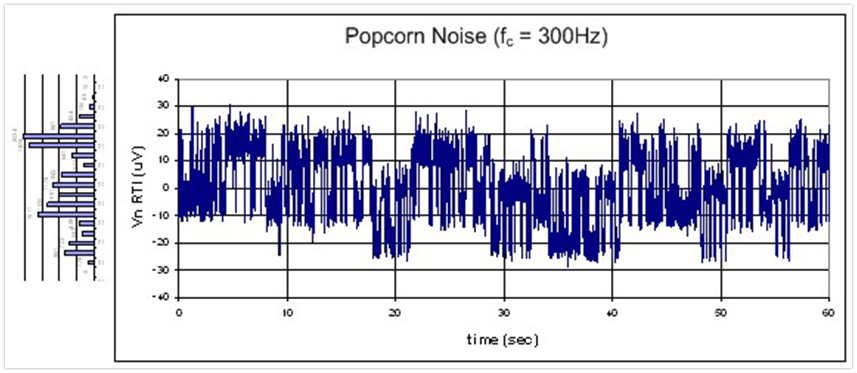
可能看這個圖一下子有點蒙,噪聲的波形倒是很直觀,但是右邊那個旋轉90°的正態分布是個什么啥意思?這就不得不說噪聲的分析方法。
c、噪聲的分析方法
我們在電路中通常需要評估電路噪聲在時域的峰峰值。但是噪聲又是一個隨機的過程,幅度隨時間變化而變化,我們沒辦法預估一個噪聲信號在某一個時刻的瞬間值,所以我們是在統計學的基礎上對噪聲進行分析的。
啥叫在統計學的基礎上分析呢?就比如我們丟硬幣,正面和反面是隨機的,沒法預先知道我們下一次丟硬幣到底是正面還是反面,但是我們知道各自的概率是50%,如果實驗次數足夠多,那么最終正面和反面的次數各占總次數的50%。
現在我們評估的噪聲也是隨機的,我們也沒辦法知道下一刻噪聲信號具體長什么樣子,但是我們可以評估,如果我們拿示波器去采樣這個信號的話,會知道它落在某一個電壓范圍的概率是多少,根據這個概率信息,我們可以推斷出我們的噪聲的峰峰值是多大。
在電路分析中,使用概率分布函數將均方根噪聲轉化為峰峰值噪聲。如下圖,左邊為噪聲的時域波形,右邊為高斯分布,高斯分布也叫正態分布。
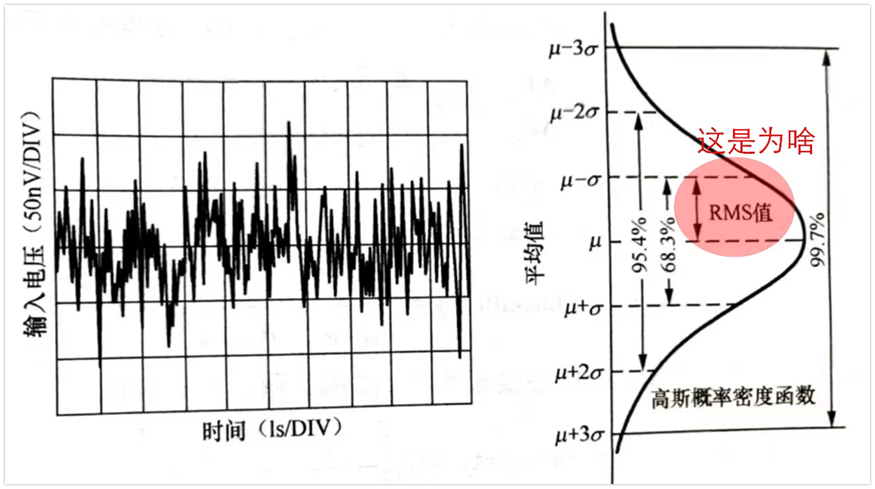
正態分布有兩個參數,一個叫期望值μ(也叫平均值),另外一個參數叫標準差σ,圖中有一個非常重要的地方,那就是RMS值等于標準差σ(μ=0)。
d、為啥噪聲的有效值Vrms等于其正態分布的標準差σ呢?
這可以從有效值的這個詞的意義里面推導出來。
有效值:如果某個交流電,與某個電壓的直流電熱效應相等,那么就可以認為該直流電的電壓就是這個交流電電壓的有效值。
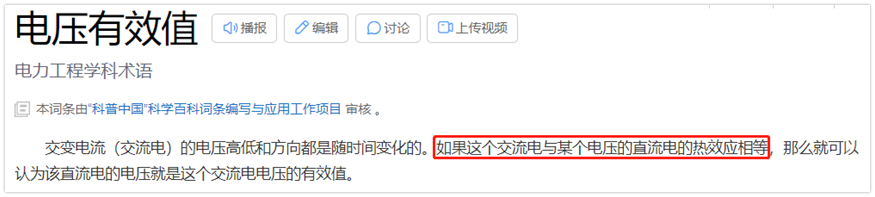
從有效值的定義看,有效值是熱效應的等效,也就是針對做功來說的。
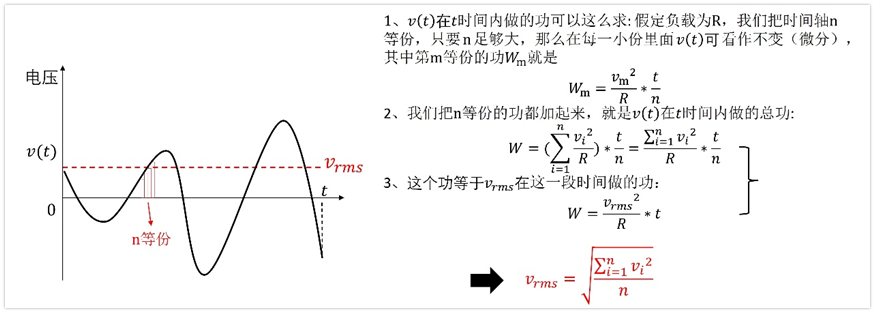
我們再看標準差的公式:
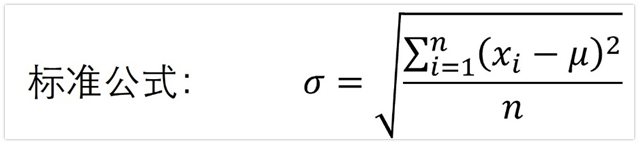
前面說了,噪聲電壓符合高斯分布,用統計學的方法來看,有下面的推導過程:

以上過程只是為了理解一句話:噪聲的有效值Vrms等于其正態分布的標準差σ。
上面推導過程看著有點費勁,看不明白記住也行,這也不是本節內容的重點。
總之,我們就是知道了:噪聲電壓的有效值等于其正態分布的標準差σ,那這有什么用呢?
回到我們的目標——我們要知道噪聲的峰峰值有多大。
我們通常可以計算出噪聲的有效值有多大,但這不是我們的最終目的,我們的最終目的是要知道噪聲的峰峰值有多大,這是我們設計電路時更關心的。在我們知道了有效值,那么也就知道了噪聲電壓對應正態分布的標準差,最終我們就能知道某個時刻噪聲電壓在某個范圍內的概率有多大。
還記得大學教材《概率論與數理統計》最后面附表里面的“標準正態數據分布表”嗎?我在網上找了一個更為精確的正態分布表,精確到了小數點15位,如下圖:
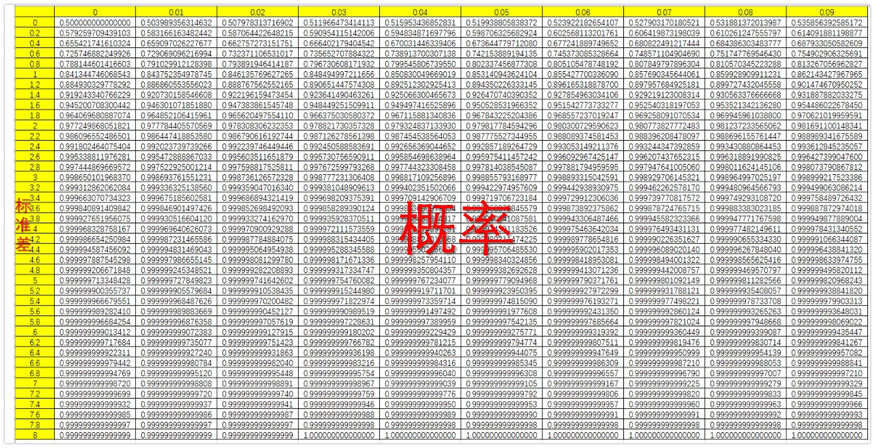
我們可以從中得到峰峰值電壓小于某一個值的概率,如下表所示:
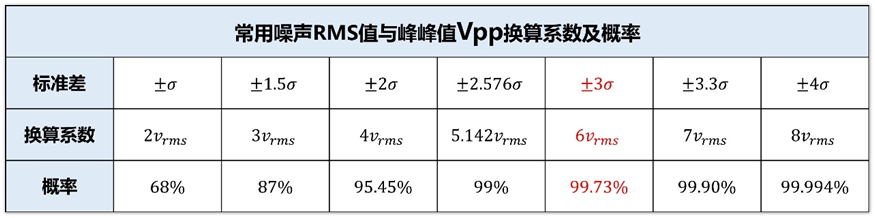
可能還是不太明白這個表是啥意思?簡單說就是,我們對有效值為Vrms的噪聲進行采樣,其采樣值落在-σ到+σ之間的概率是68%,落在-2σ和+2σ之間的概率是95.45%,落在-3σ和+3σ之間的概率是99.73%。這意味著幅值很大的電壓值出現的概率很小,比如落在-4σ和+4σ的概率是99.994%,即電壓超過±4σ的電壓出現的概率是0.006%,這個概率是很低的。如果我們拿示波器去測量這個電壓,在示波器界面可能是看不到超過±4σ的電壓信號的,畢竟示波器采樣的數據量有限,除非說我們觀察非常久的時間,可能捕捉到一個更高的電壓信號,但通常我們也不會這么干。
從前面的正態分布表也可以知道,采樣值落在8σ內的概率已經是99.9999999999999%,也就是說電壓值超出±8σ的概率是0.0000000000001%。
基于上面的概率問題,一般評估噪聲的峰峰值電壓是±3σ對應的換算系數,也就是認為噪聲的峰峰值為6*vrms,如果對噪聲容忍程度非常低,可以用±4σ或更高的換算系數。
以上就是使用統計學評估噪聲的基本原理,到這里已經可以回答前面的問題1:
問題1:白噪聲是隨機的,并且是全帶寬的,如果某個時刻,正好是各個頻率的波峰疊在一起,那噪聲電壓不是無窮大?概率雖然低,但可能性是在的吧,但是我們好像不會考慮這個問題。
答:如果用統計學的方法看,因為正態分布兩邊是無限延伸的,這種情況也是存在的。但可以想象,出現這種概率是有多么多么的小,畢竟噪聲電壓在±4σ外的概率已經低到了0.006%。從前面15位精度的正態分布表看,到了±8σ的概率已經低到了0.0000000000001%,至于問題里面無窮大電壓的場景,應該只具有數學上的可能性,現實中是不會出現的了。
為了避免沒抓到重點,這里先小結一下:
電壓噪聲服從高斯分布(正態分布),并且其有效值Vrms就對應高斯分布的標準差σ。再結合高斯分布的特性,我們一般可以認為電壓不超過±3σ,即電壓不超過6*Vrms,即評估噪聲的時候,可以按照噪聲電壓峰峰值為6*Vrms。
到這里,那么剩下的問題就是如何計算噪聲的有效值Vrms了。
器件一般以頻譜密度的方式給出,比如下面是ti的芯片tlv9061給出的噪聲參數:

可以看到,噪聲的大小是跟頻率有關系的,不同頻率段的噪聲大小不同。除此之外,除了0.1Hz~10Hz是直接以峰峰值給出的,單位是uVpp,這個理解起來完全沒問題。另外兩個,一個是電壓噪聲密度,單位是nv/(根號Hz),另外也是fA/(根號Hz),理解起來就相對困難,我就想廠家為什么這么給參數呢?直接像0.1Hz~10Hz這樣給出峰峰值大小不香嗎?這是故意要提高使用門檻嗎?
e、噪聲參數為什么以根號hz的方式給出?
可以看到,上面是芯片tlv9061規格書中表格的數據,其規格書也給出了噪聲參數的曲線,我們來看一下。
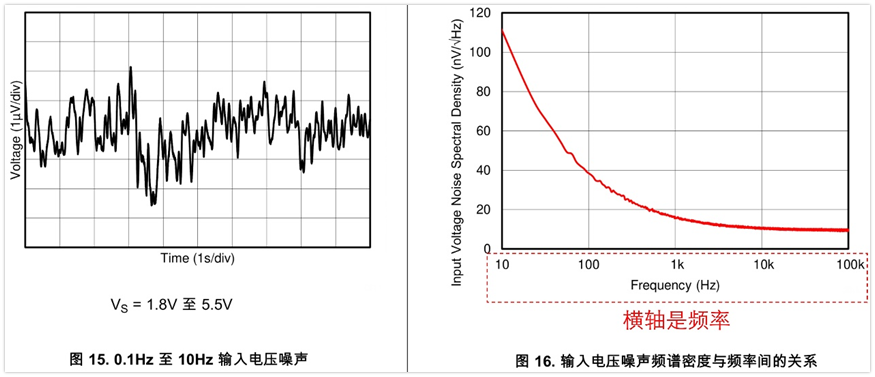
看右邊的圖,橫軸是頻率,縱軸是電壓噪聲頻譜密度,下面來看下其物理意義吧。

以上解釋了為什么噪聲電壓密度的單位為什么是V/根號Hz,如果要用簡短的話概括,那就是:電壓有效值是針對做功來說的,而做功相關的參數就是功率譜密度,單位是V^2/Hz或A^2/Hz,功率譜密度開方就是電壓/電流幅度譜密度(假定負載是1Ω),單位是:V/根號Hz和A/根號Hz。
需要注意,上面的推導非常的不嚴謹。要想真正嚴謹的理解,需要去看大學教材《信號與系統》的第6章節。
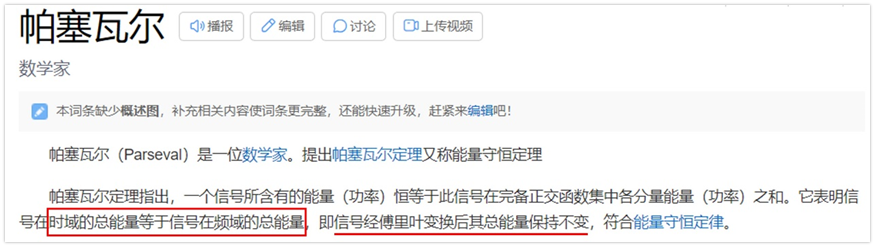
值得一提的是,第1步到第2步用到了帕斯瓦爾定理:
現在我們已經知道了上圖中的電壓噪聲頻譜密度的物理意義,那么如何將這個轉化為Vrms值呢?
f、如何將電壓噪聲頻譜密度轉化為Vrms
其實這個轉化在上面圖片中第3步已經寫明了,就是這個式子:

需要注意,上面的積分范圍0~∞,是全帶寬積分,實際應用中要根據實際的頻率范圍。看著這個公式不是很直觀,下面就以運放為例子來畫一個示意圖吧。
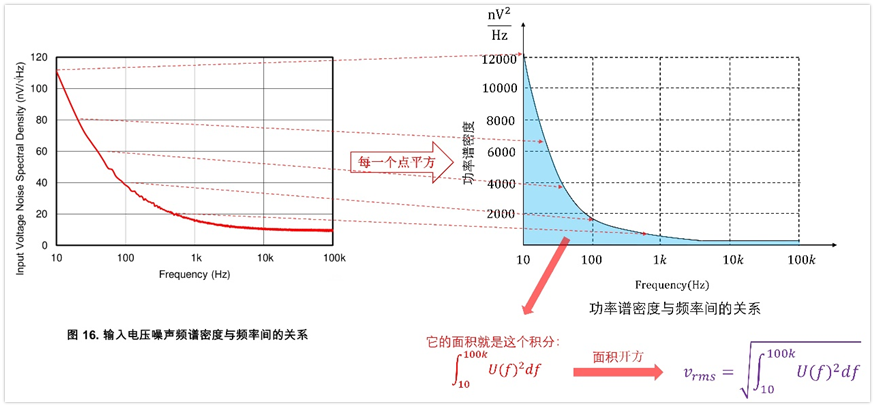
根據運放手冊提供的電壓噪聲頻譜密度,我們將每一個點進行平方,就可以得到右邊的功率譜密度,然后在頻率上進行積分,這個積分過程就等效為求圖中陰影部分的面積,然后我們將求得的面積進行開方,就能得到噪聲電壓的有效值了,圖中計算了從10hz~100Khz帶寬內的噪聲電壓有效值。
實際應用中,我們通常不會求全帶寬的,因為實際電路也不是全帶寬的,我們實際通常求的是一段帶寬范圍內的,因此,常用的是下面這個:

上面的過程看著很復雜,只是為了說明最基本的原理,實際評估運放噪聲會有一些近似的辦法的,這個后面會講。
總之,將電壓噪聲頻譜密度轉化為有效值的原理就是:將電壓噪聲頻譜密度進行平方,轉為功率譜密度,然后在帶寬范圍內積分(求面積),再開方,就能求得有效值電壓了。
g、如何將電流噪聲頻譜密度轉化為Irms
電流噪聲頻譜密度轉為電流有效值Irms,其實原理和電壓噪聲頻譜密度的轉換一樣,因為功率P=U^2/R,也等于P=I^2*R,如果按照前面的過程推一遍,電阻R也是可以消掉的,最終可以求得電流有效值為:

3、兩種噪聲源
說完了如何將噪聲電壓頻譜密度轉化為有效值電壓Vrms,以及如何將電流噪聲頻譜密度轉化為有效值電流Irms的原理及公式。
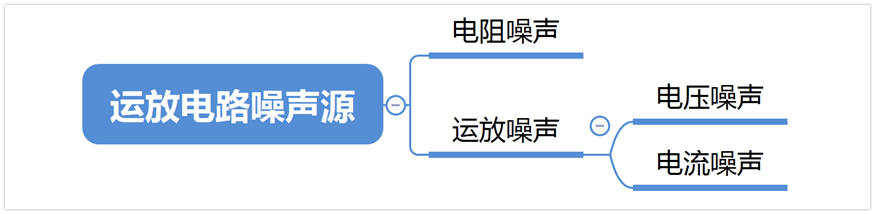
還有個問題,那就是運放電路到底有哪些噪聲需要評估呢?只有運放的噪聲需要評估嗎?
噪聲我們一般要評估兩種,一種是運放的噪聲,一種是電阻的噪聲。
下面來繼續具體說下如何將它們轉化為Vrms和Irms。
4、運放本身的噪聲Vrms,Irms計算
運放的噪聲有電壓噪聲和電流噪聲,如下圖是ti的運放芯片tlv9061給出的噪聲參數,給出的是電壓噪聲頻譜密度和電流噪聲頻譜密度。

也給出了對應的電壓噪聲密度曲線:
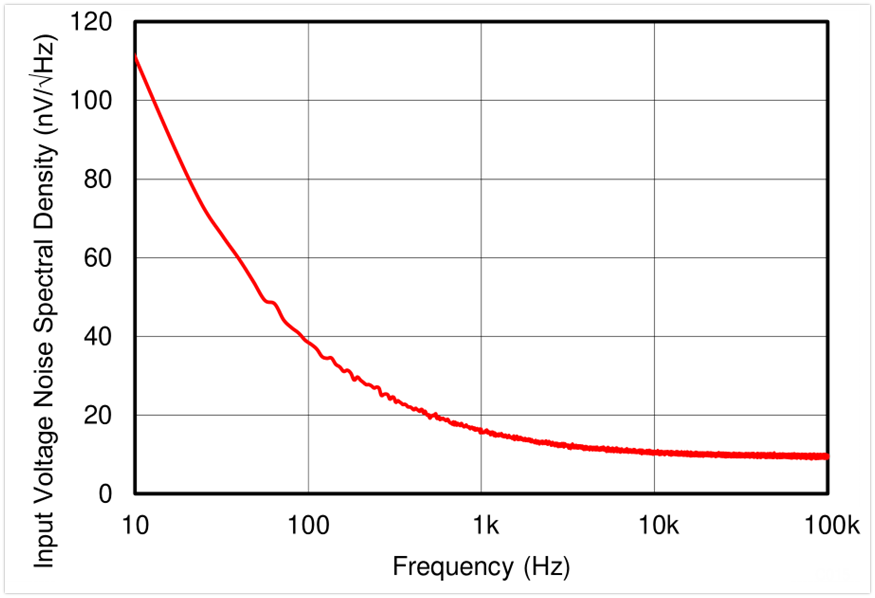
前面我們已經知道了求運放噪聲的基本原理:將噪聲電壓頻譜密度進行平方,轉為功率譜密度,然后在帶寬范圍內積分(求面積),再開方,就能求得有效值電壓了。
問題是這個求面積可操作性實在是太差了,這個面積很不好求,那么有什么辦法呢?
辦法自然是有,那就是將上面的曲線分成兩部分,分別是1/f噪聲和寬帶噪聲,如下圖所示。
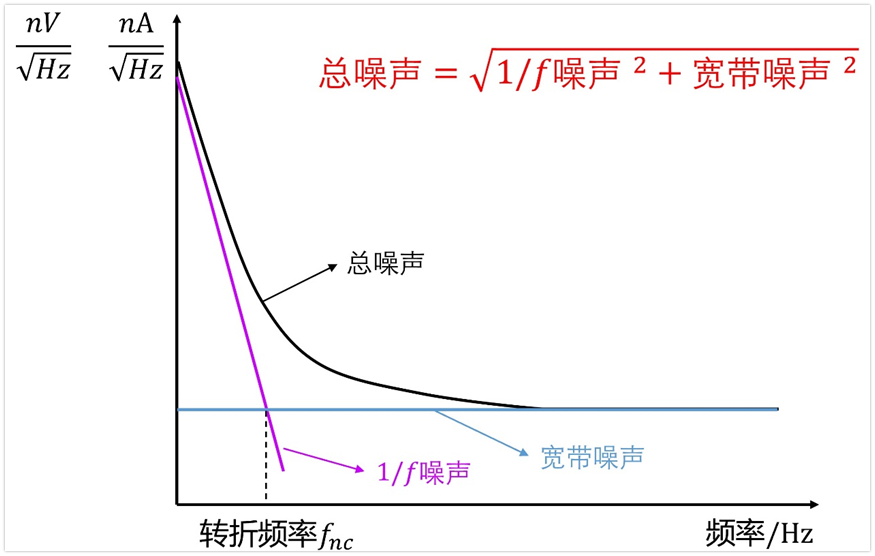
我們在手冊中看到的電壓噪聲頻譜密度曲線可以看作是1/f噪聲和寬帶噪聲的疊加(平方后相加再開根號),疊加起來之后的曲線看起來不規則,導致我們難以計算。所以真正計算噪聲的時候,我們又需要將這個噪聲分解為1/f噪聲和寬帶噪聲兩部分。
a、寬帶噪聲Vrms_bw的計算
因為寬帶噪聲曲線是平的,很好計算,就先看寬帶噪聲的計算方法吧。
既然寬帶噪聲密度曲線是平的,也就是說其是一個常量,用字母B來表示吧,那么其在頻率fa~fb頻帶內的噪聲可以用下面公式計算:

舉個例子:求tlv9061在0.1Hz~100Khz頻帶內的寬帶噪聲電壓有效值?
首先從曲線上看出,在10Khz以后,噪聲電壓頻譜密度為10nV/根號赫茲,這個就是寬帶噪聲電壓頻譜密度,即對應上面公式的B=10nV/根號赫茲。
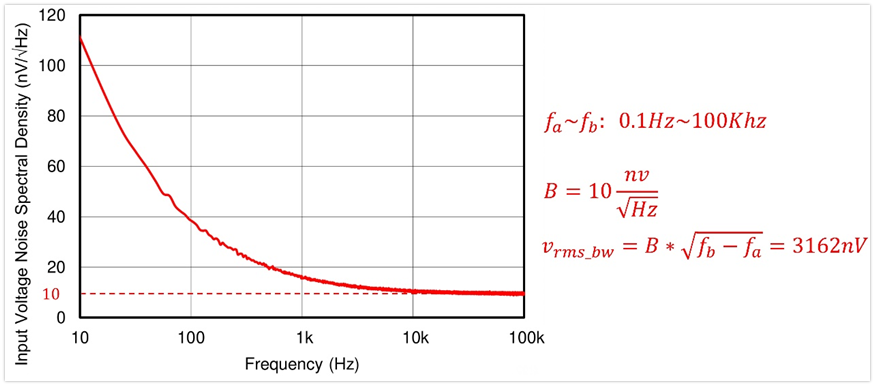
套用上面的公式,最終可求得在0.1hz~100Khz帶寬內的寬帶電壓噪聲有效值為3162nV。
b、1/f噪聲Vrms_1/f的計算
再看看啥叫1/f噪聲。
顧名思義,1/f噪聲,說的就是功率譜密度曲線與頻率之間滿足1/f的規律,注意,這里是功率譜密度,不是電壓頻譜密度。如果是電壓頻譜密度,那么就是滿足1/(根號f)的規律。
如果在頻率1Hz處的1/f電壓噪聲頻譜密度是A,那么根據1/f的規律,頻率f處的1/f電壓噪聲頻譜密度值有如下關系式:
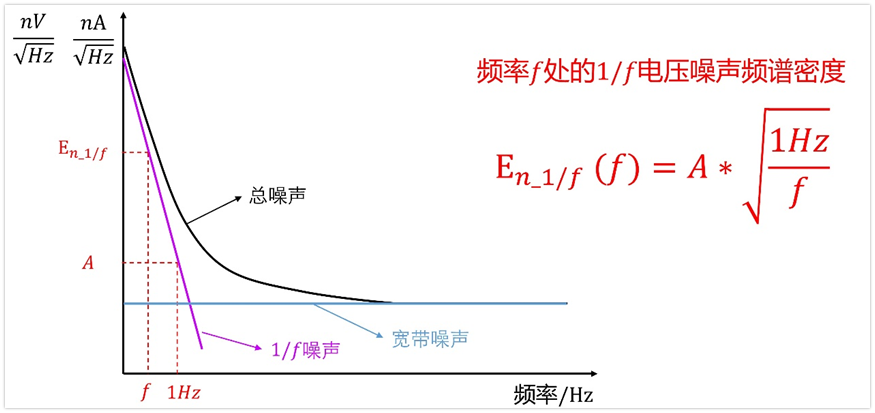
根據上面這個式子,我們就可以得到一定頻率范圍內1/f電壓噪聲的有效值,計算方法如下:

還是以tlv9061舉例子:求tlv9061在0.1Hz~100Khz內的1/f電壓噪聲有效值?
規格書中只給了10Hz~100Hz的電壓噪聲頻譜密度曲線,因此,無法直接從圖中得到1Hz的電壓噪聲頻譜密度A,規格書的數據表格也沒有提供這個參數,那怎么辦呢?
其實我們可以從1/f噪聲的定義推測出來,我們可以先求得10Hz處的1/f噪聲,然后根據前面的1/f噪聲頻譜密度公式推算出來A的大小。
具體過程如下:
首先從曲線上面可以得到10Hz處的總的電壓噪聲頻譜密度為:E10hz(總)=110nV/根號hz,然后我們又知道10Hz出的寬帶電壓噪聲頻譜密度為:10nV/根號hz。再根據疊加關系,就可以得到10Hz處的1/f噪聲。
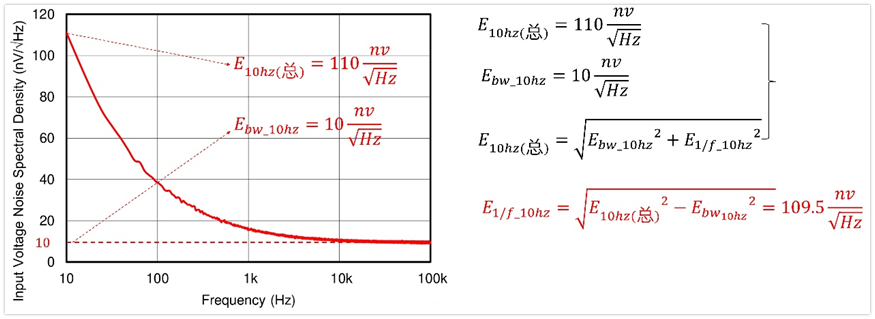
然后根據前面的1/f電壓噪聲頻譜密度公式可求得A的值,再利用Vrms_1/f公式求得最終的噪聲電壓有效值為1286nV。

c、總電壓噪聲Vrms計算
前面我們將噪聲分解為1/f噪聲Vrms_1/f和寬帶噪聲Vrms_bw,現在已經知道怎么求各自的有效值了,現在還需要將它們合并,求最終的噪聲電壓有效值。
也很簡單,只需要將它們平方之后相加再開根號就可以了,注意,不要直接將兩個電壓值相加。

為什么不是直接相加?
其實也可以從電壓做功的角度考慮,因為做功電壓是要平方的,如果直接相加,那么分別計算做的功相加,和電壓先相加再計算做的功必然不相等。比如如果二者都是1V,那么分別在R上做的功為:1V*1V*R+1V*1V*R=2R;電壓相加做的功:(1V+1V)*(1V+1V)*R=4R,兩者是不相等的。
所以按照前面的例子,1/f電壓噪聲有效值是1286nV,寬帶電壓噪聲是3162nV,那么最終的總電壓噪聲有效值就是他們倆和的平方根,即3413nV。

e、總電流噪聲Irms計算
上面舉的例子都是電壓噪聲Vrms計算,其實電流噪聲Irms也是一樣的,也是分別計算1/f電流噪聲和寬帶電流噪聲,然后將兩者計算平方和根即可。

不過因為前面舉例子的芯片tlv9061沒有給全電流噪聲參數,只有一個1Khz的電流噪聲密度值,也沒有對應的曲線,所以沒辦法具體計算。

至于廠家為什么沒有標出來,那是因為這個放大器CMOS型放大器,電流非常小,電流噪聲就更小了。從上表可以看出,這顆放大器的電壓噪聲是nV級,而電流噪聲是fA級,中間還隔著pA級,也就是說,電流噪聲遠小于電壓噪聲,因此電流噪聲可以忽略掉。
為了說明電流噪聲Irms如何計算,還是舉個例子吧。
因為手冊中只給出了1Khz時的電流噪聲頻譜密度為23fA/根號赫茲,從噪聲頻譜密度曲線形狀上我們知道,在低頻時噪聲密度值隨頻率升高而下降,高頻時噪聲密度隨頻率基本不變,其約等于寬帶噪聲。由此我們知道這個放大器的寬帶噪聲密度肯定是小于23fA/根號赫茲的,我們暫且就用23fA/根號赫茲這個參數計算寬帶噪聲,知道這個計算出來的值要比實際情況大就好。
最終計算0.1Hz~100Khz的寬帶電流噪聲有效值Irms_bw為7.3nA,計算過程如下

d、帶寬確定
到這里已經說明了如何求得fa~fb頻帶內的噪聲有效值,那問題來了,為什么不求0~∞帶寬的噪聲有效值呢?而只求一部分?
下限頻率fa
為什么下限頻率fa不能是0呢?
這是因為,我們是從統計學的方法分析的噪聲,如果最低頻率為0,那么意味值時間為無窮大,這顯然不符合常理。另外一方面,如果fa=0,那么其電壓噪聲頻譜密度為無窮大,這也是沒法計算的。
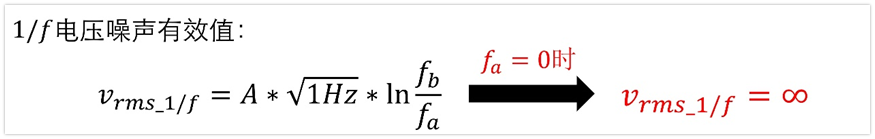
工程上認為,當噪聲頻率低于0.1Hz,即10s以上發作一次的事件,一般可以被認為是人為、環境因素帶來的擾動,這可能與運放電路本身無關。因此,絕大多數情況下,計算1/f噪聲,下限取值為0.1Hz。
上限頻率fb
上限頻率fb為什么不能是無窮大呢?
首先,如果上限是fb,那么不論是1/f噪聲,還是寬帶噪聲,最終的結果都會是無窮大,這也是不符合常理的。
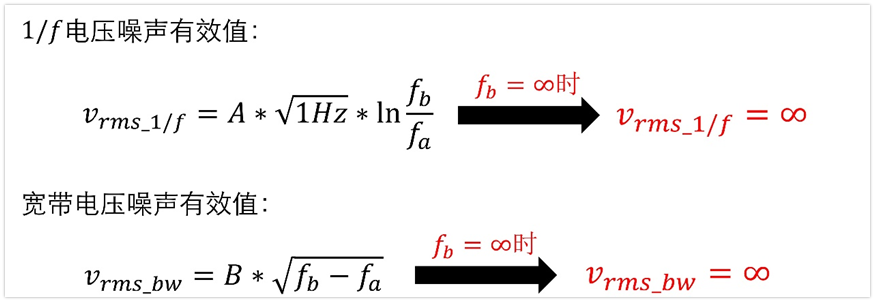
另外一方面,我們的運放電路本身都是有上限截止頻率的,類似于一個低通濾波器,還記得運放有一個參數增益帶寬積GBW嗎?頻率到一定程度,運放都放大不了信號的。
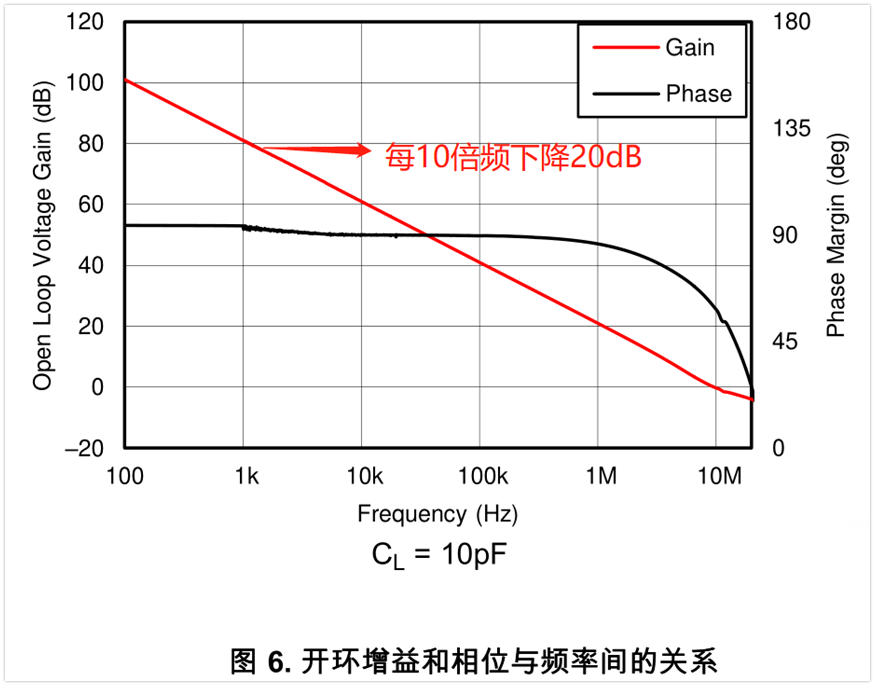
如下圖是tlv9061的開環曲線,頻率超過100Hz之后, 每10倍頻下降20dB,這個特性跟一階低通濾波器是一樣的。
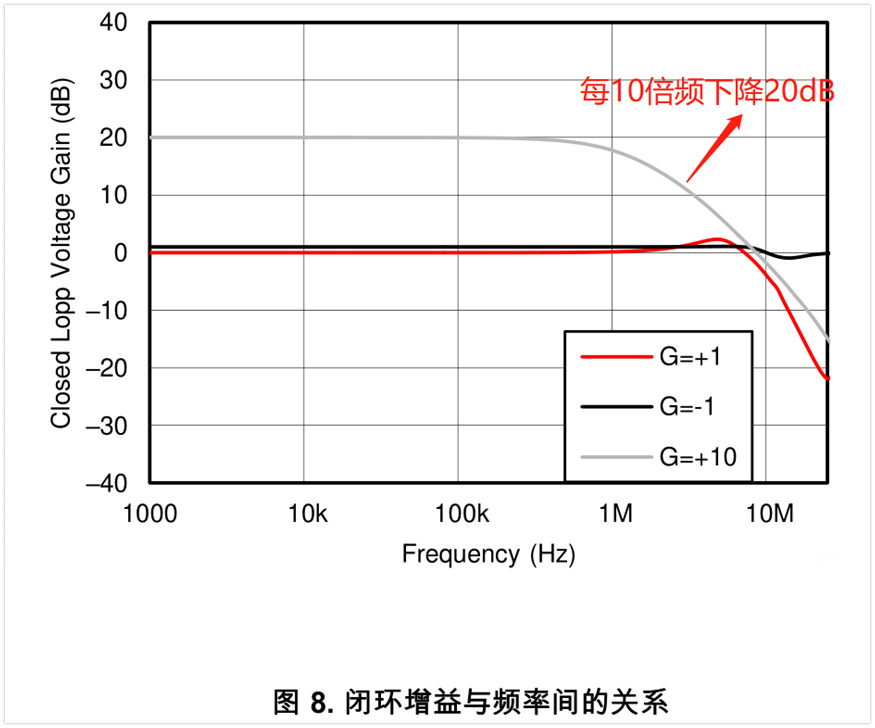
當然,運放一般不是在開環的時候用,我們再看看閉環電路的增益情況。下圖是tlv9061手冊中的閉環增益曲線,可以看到,閉環增益為10倍時,在1Mhz以后,也是每10倍頻下降20db,其曲線像是一個截止頻率為1Mhz的低通濾波器。
總之,我們在使用運放的時候,其最終的幅頻特性就類似一個低通濾波器,其截止頻率就是閉環的帶寬。這個濾波器也會濾掉高頻的噪聲,所以說評估噪聲的時候,不能認為噪聲上限是無窮的,我們要確定好上限頻率fb。
那問題來了,上限頻率是等效濾波器的截止頻率嗎?
答案是否定的,因為濾波器的截止頻率一般說的是3db的,3db往后噪聲只是被衰減了,并不是沒有了。
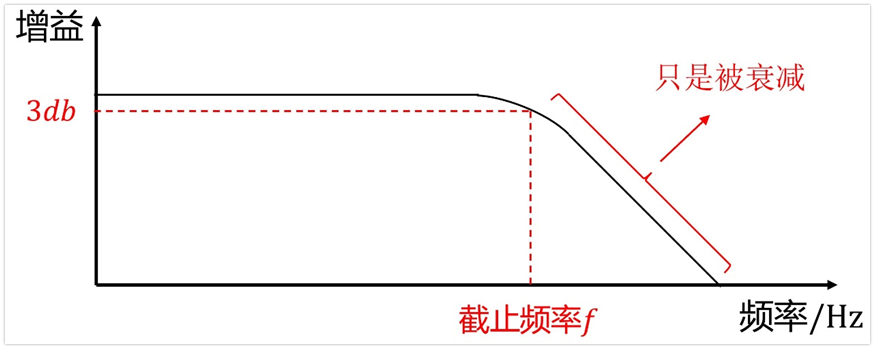
如果說高于截止頻率之后,增益立馬變為0,那么上限頻率等于截止頻率沒問題,但問題是現在這個濾波器并非磚墻濾波器(頻帶內完全不衰減,頻帶外完全衰減為0),所以,如果我們直接草率的讓上限頻率fb等于截止頻率,那么是不符合實際的。
可能會有同學認為,截止頻率之后看著幅度衰減很快,忽略也不要緊吧?其實不然,因為這是個對數坐標軸,也就是說頻率增大10倍才下降20db,從截止頻率下降20db的頻率范圍其實很寬,因此不能忽略。
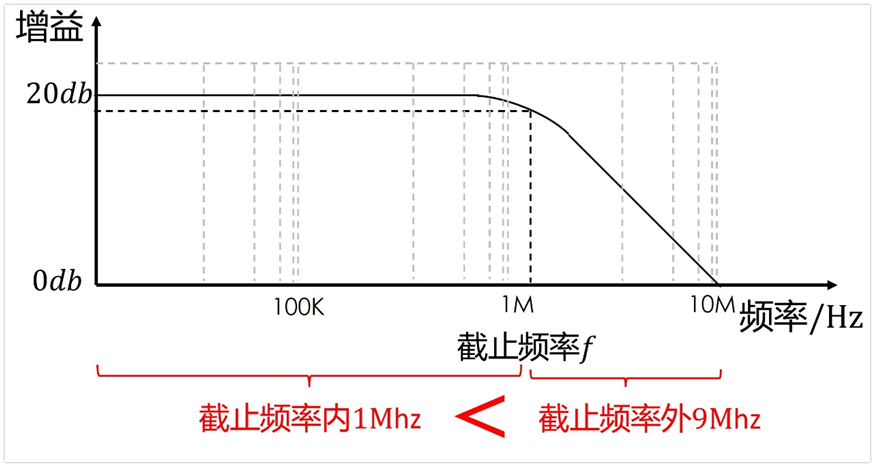
既然問題不能忽略,那又尬住了,這個上限頻率fb咋辦?
可以用等效的方法,原理如下:假設有一個磚墻濾波器,其截止頻率為fh,如果其帶寬內的噪聲電壓有效值等于這個濾波器的噪聲電壓有效值,那么我們就可以把這個fh看作是我們要的上限頻率fb。
結合前面鋪墊的基礎,只需要讓下面兩部分的面積相等,就能求得fh和f截止的關系,進而就能求得上限頻率fb=fh了(注意,下圖的縱軸是電壓頻譜密度的平方,并不是增益曲線,其形狀應該是增益平方后對應的形狀)。
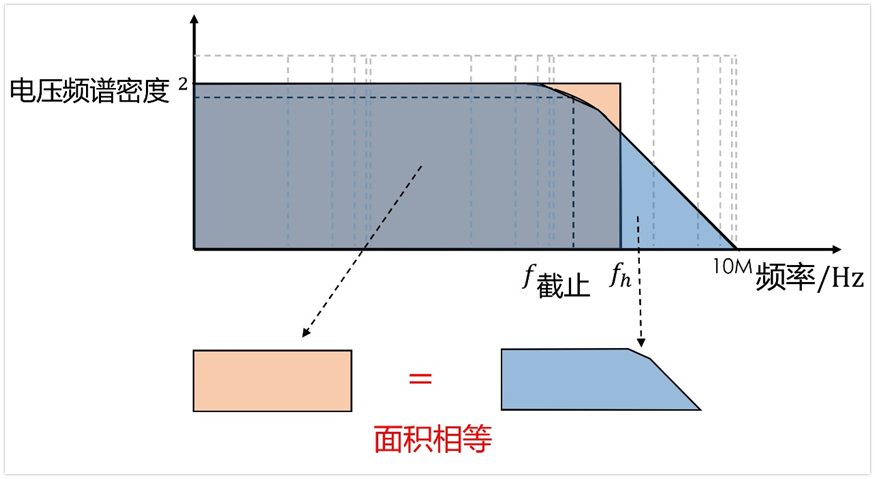
后面的等效計算完全就是個數學問題,這里就不推導了,直接拿結論來用吧,fh=1.57*f截止,即上限頻率是濾波器截止頻率的1.57倍。
注意,這里的數學計算是將噪聲看成是寬帶噪聲來算的,忽略了1/f噪聲,因為在高頻段,1/f噪聲的貢獻本身非常小,所以忽略是沒問題的。
其次需要注意,如果我們的電路本身就是濾波器電路,并且階數不是一階,那么這個系數也需要對于的變化。這應該比較容易明白,如果是高階濾波器,那么曲線更陡峭,更加接近于磚墻濾波器,其系數應該更小。
下面是各種濾波器的系數:

舉個例子:現用tlv9061設計了一個放大5倍的放大器,電路本身并非是濾波器電路,請問其評估噪聲的時候帶寬是多少?
答:如前面的分析,頻率下限按照fa=0.1Hz;查看手冊,TLV9061的增益帶寬積是10Mhz,放大倍數為5倍,所以其閉環增益帶寬為:10Mhz/5=2Mhz,這個電路本身并非濾波器,因此等效為一階濾波器,截止頻率為2Mhz,再乘以一階濾波器的系數1.57,可求得頻率上限fb=1.57*2Mhz=3.14Mhz。
總之,我們在評估帶寬的時候,下限可以按照0.1Hz來評估。上限要看電路本身是否是濾波器,如果不是濾波器,可以先求得對應的閉環帶寬,然后乘以對應的系數,就能得出上限頻率了;如果是低通濾波器,則直接用濾波器的截止頻率乘以對應的系數,也能得到上限頻率。
5、電阻的噪聲Vrms_r的計算
關于運放的噪聲已經說明白了,那么電阻噪聲呢?
電阻噪聲一般說的是熱噪聲,也是白噪聲,其特點是各個頻率的噪聲能量相同,即噪聲密度是一條平坦的曲線。它的RMS值與帶寬的平方根成正比,隨著帶寬的增加,電阻的噪聲會成為電路噪聲的主要因素。
電阻的電壓噪聲有效值計算相對簡單,只跟電阻阻值的大小,溫度,帶寬三者有關,可以用下面公式計算:

我們也可以根據上面的公式,反推得到電阻的電壓噪聲頻譜密度公式,下圖即是電阻的電壓噪聲密度公式,以及常見電阻在25℃下的電壓噪聲頻譜密度。
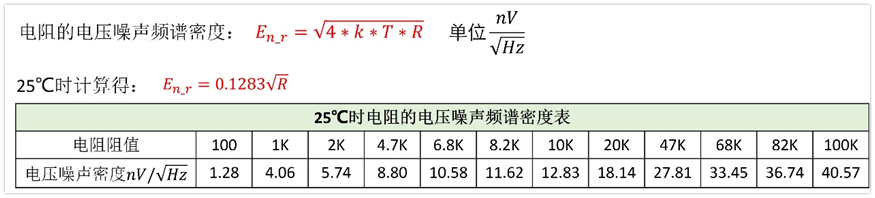
實際電路設計中,我們可以根據上表快速的近似估算電阻的噪聲大小。
根據上面的公式,我們可以推導出:無論并聯,串聯,只要最終總的電阻阻值一致,都是不會改變電阻的熱噪聲的,過程就不證明了。
6、總的電壓噪聲輸出計算
至此,我們已經知道如何求得運放,電阻各自的電壓噪聲有效值,但這還不是我們最終的目的,我們需要知道的是我們設計的電路輸出的總的電壓噪聲大小。
其實后面就簡單了,我們只需要將噪聲源加到電路當中去就可以了,然后利用疊加原理分別計算不同噪聲源對輸出噪聲的貢獻,最后就可以求得最終輸出端的總噪聲大小了。
a、放大器電路噪聲模型
下圖是常見的同相放大器放大電路:
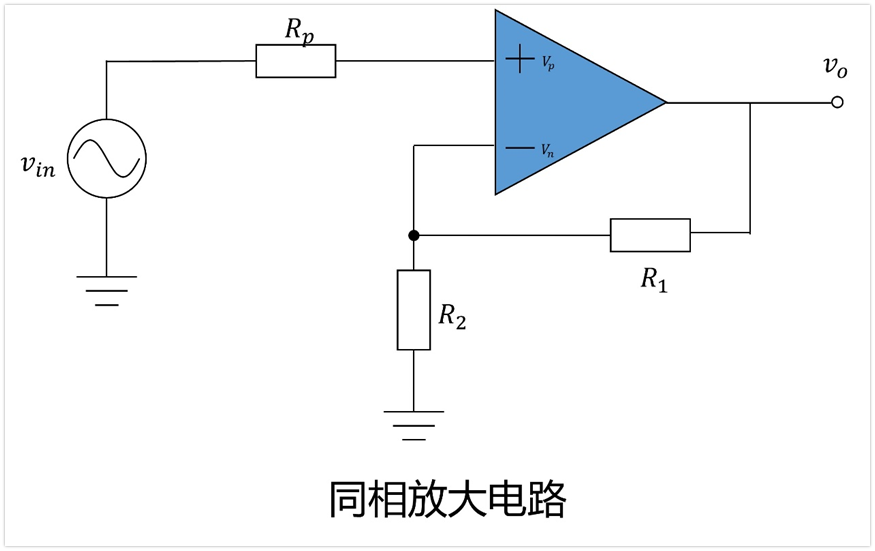
我們給每個電阻加上電壓噪聲,給放大器加上電壓噪聲和電流噪聲,最終可構建如下圖所示的電路噪聲模型。
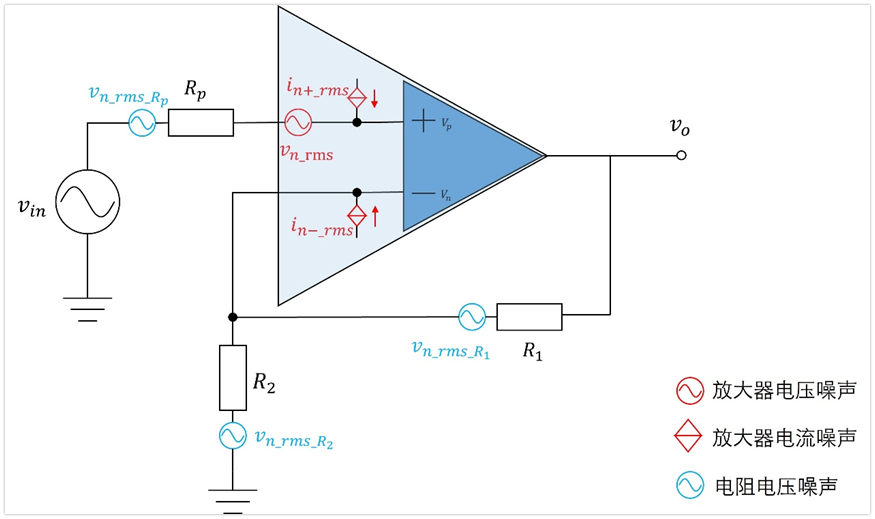
這里需要提一點,我們前面已經知道了運放的電流噪聲有效值Irms如何計算,但是這個模型里面是有兩個電流噪聲的,分別是同相端電流噪聲in+_rms和反相端電流噪聲in-_rms,一般我們認為計算出的電流噪聲Irms=in+_rms=in-_rms。
加上所有的噪聲信號之后,這個電路看起來非常復雜,看著有點頭大,那么輸出端總的電壓噪聲該如何計算呢?
b、放大器電路的總噪聲有效值Vn_rms_out
其實開頭已經說了,我們只需要將噪聲源加到電路當中去就可以了,利用疊加原理然后分別計算不同噪聲源對輸出噪聲的貢獻,就可以求得最終輸出端的總噪聲大小了。
具體如何求呢?
上圖中有3個電阻,就有3個電阻電壓噪聲,然后放大器同相和反相端各有1個電流噪聲,還有一個運放的電壓噪聲,總共6個噪聲源,我們要分別求這6個噪聲源在輸出端產生的噪聲大小。
因為我們電路是線性電路,因此滿足疊加原理,可以求得6個噪聲的表達式如下,然后將這些噪聲求平方和,然后開根號,就能得到我們最終總的輸出電壓總噪聲Vn_rms_out了。
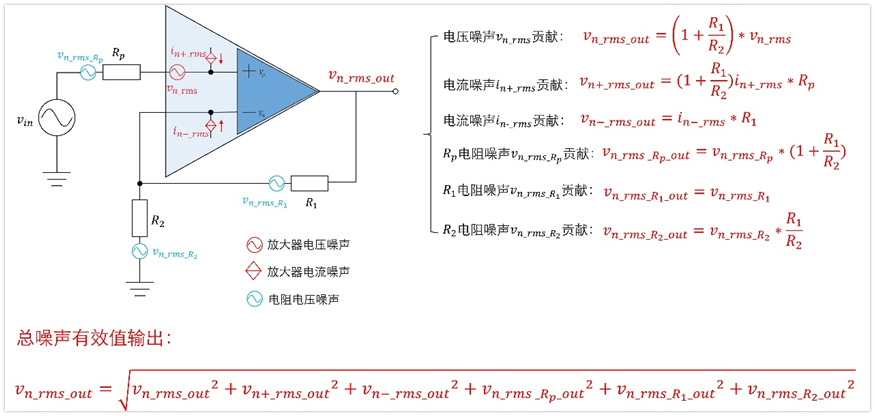
這里有個問題,不是利用疊加原理嗎?為什么最終總的電壓噪聲有效值不是將這6個直接加起來呢?而是取平方,累加之后再開方呢?
其實原理跟1/f噪聲和寬帶噪聲疊加的原理一樣,我們現在計算的6個噪聲都是有效值,合并之后計算總的輸出也是有效值,既然都是有效值,那么就是疊加后要滿足做功相等,所以就是平方后累加再開方。
下面寫明了如何求得6個噪聲的表達式,其實如果對運放的虛短和虛斷理解清晰,應該就不在話下了。
1、放大器電壓噪聲Vn_rms對輸出端的貢獻Vn_rms_out
單獨評估放大器電壓噪聲Vn_rms對輸出端的貢獻,那么我們令其它的噪聲不存在,電壓噪聲統統視為短路,電流噪聲通通視為斷路。同時我們是評估噪聲的影響,那么令輸入信號也為0,即輸入接地,最終等效電路如下圖:
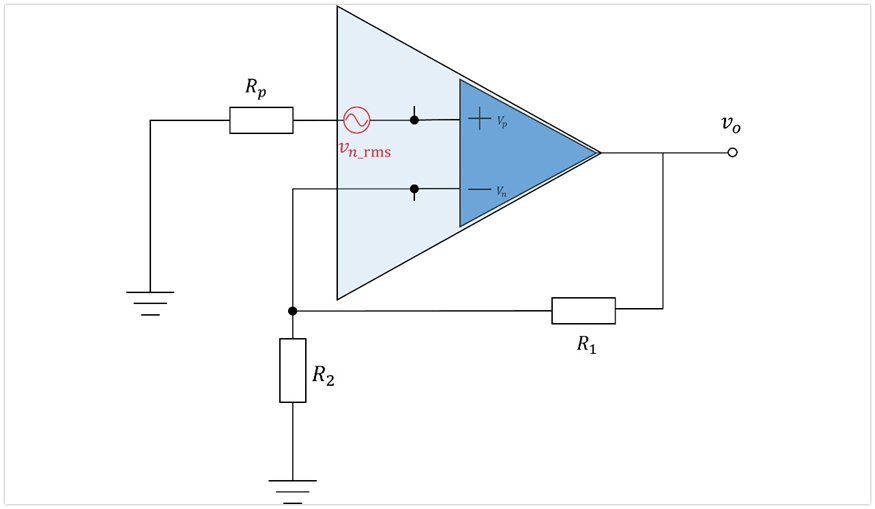
根據運放的基本特性,我們很容易就能求出Vn_rms在輸出端的貢獻電壓了,過程如下:
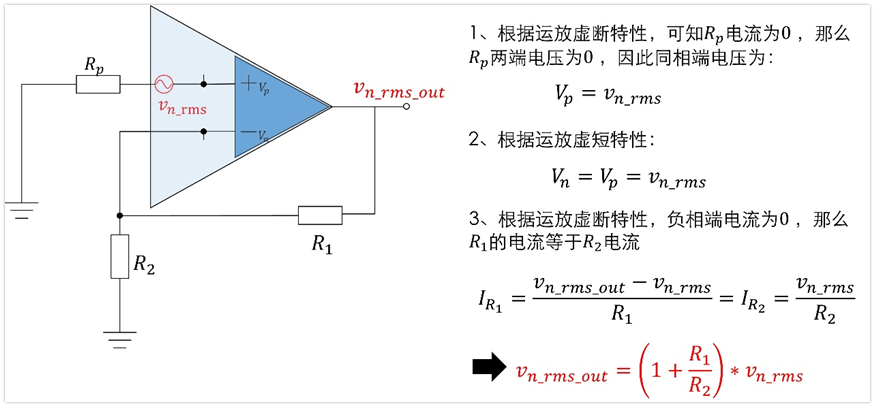
上面這個電路其實就是個常見的同相放大電路,放大倍數就是1+R1/R2,輸入信號是Vn_rms,上面的過程我只不過是按照運放虛斷和虛短的基本特性又推導了一遍而已。
繼續看剩下的5個噪聲對輸出的貢獻。
2、放大器正相端電流噪聲In+_rms對輸出噪聲的貢獻Vn+_rms_out
同樣的道理,其它的電壓噪聲視為短路,電流噪聲視為開路,輸入接地,電路圖變成如下:
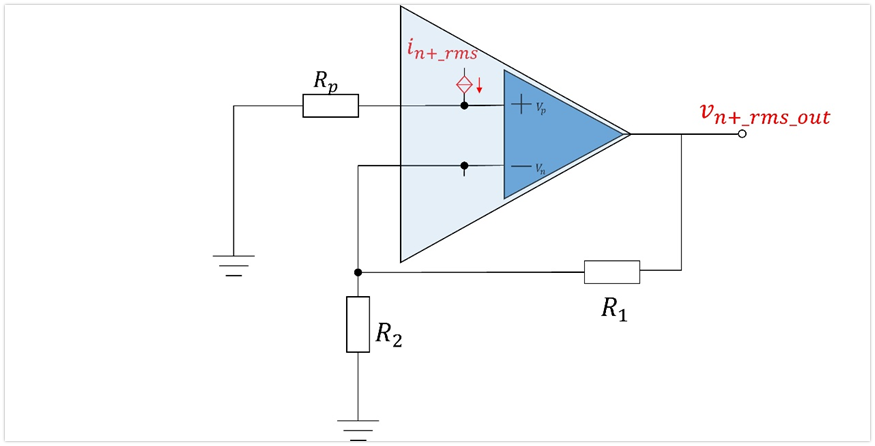
很容計算出正相端電流噪聲在輸出端的貢獻如下:
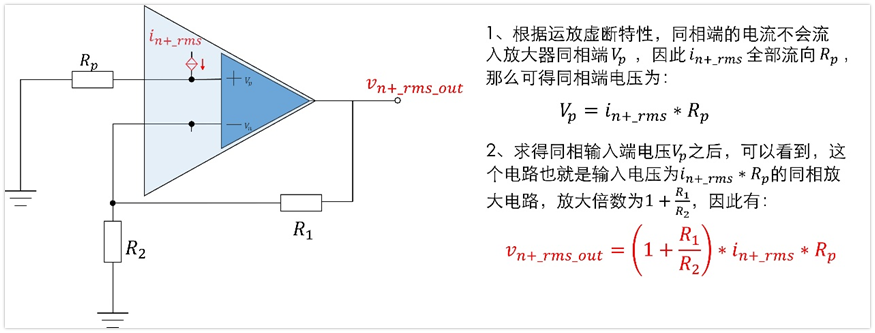
3、放大器負相端電流噪聲In-_rms對輸出噪聲的貢獻Vn-_rms_out
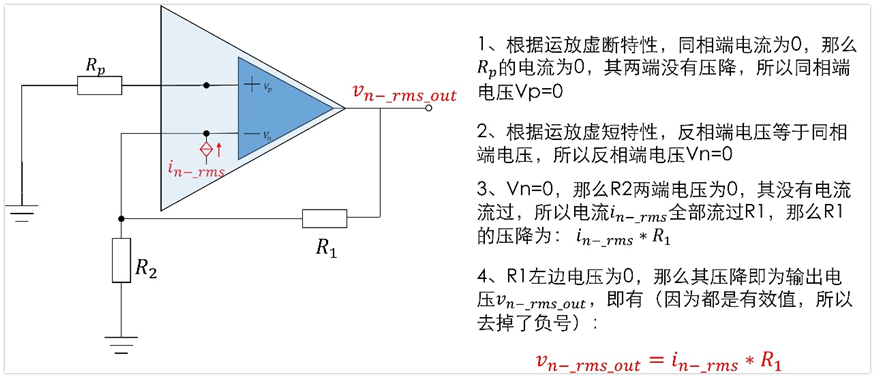
4、電阻Rp的噪聲Vn_rms_rp對輸出的貢獻Vn_rms_rp_out
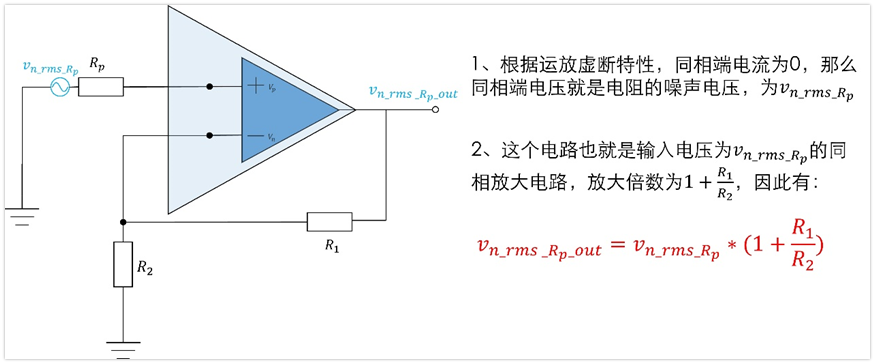
5、電阻R1的噪聲Vn_rms_r1對輸出的貢獻Vn_rms_r1_out
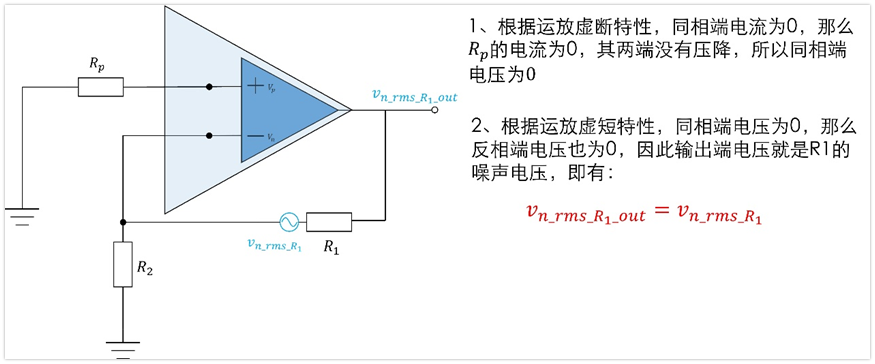
6、電阻R2的噪聲Vn_rms_r2對輸出的貢獻Vn_rms_r2_out

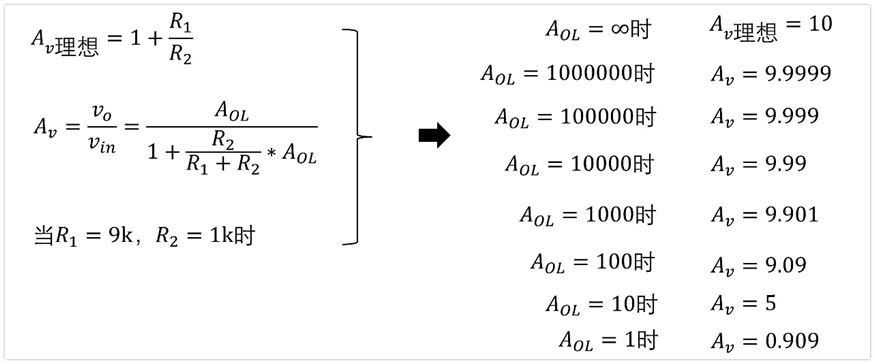
可以看到,如果運放的AoL不是無窮大,那么實際電路的閉環增益是和電阻有關系的。我們代一些具體的值進去看看影響有多大,假設R2=1K,R1=9K。開環增益從1到1百萬時,閉環增益的情況如下圖:
從上面至少可以看到兩點:
a、在AoL比較小的時候,實際增益就與理想情況下的增益有明顯差異了。比如如果AoL=1000,實際閉環增益Av=9.901,與我們想象的放大10倍就已經有1%左右的差異,如果AoL=100,實際Av=9.09,差不多有10%的差距了。
b、在AoL比較大的時候,一致性要求低。盡管AoL=100萬和AoL=10萬二者相差了10倍,但是閉環增益一個是9.9999,一個是9.999,相對于理想情況下的10來說,誤差都非常小。也就是說只要運放開環增益AoL足夠大,閉環增益都基本穩定在同一個值,正是因為這樣,我們對運放的開環增益AoL的一致性要求就很低了,只要求大就可以了,不管是50萬倍還是100萬倍,閉環增益都基本一樣。我們實際運放的AoL也確實沒那么精確。
以LM2904為例,如下圖,其典型開環增益AoL是140V/mV=14萬倍,最小值為7萬倍,如果考慮溫度,那就只有3.5萬倍,至于上限,都是沒有標出來的。總的來說,就是器件的開環增益一致性比較差,但是因為夠大,也不影響我們使用。

除此之外,我們還應該看到第3點:
c、閉環增益越大,要求AoL越大。上面是放大10倍的情況,閉環增益誤差1%時對應的開環增益是1000。假如我們放大100倍(即設計閉環增益=100倍),要求實際運放閉環增益與理想運放只有1%的差距,那么需要AoL≈10000(此時閉環增益Av=99)。相對于10倍只需要AoL=1000,此時AoL=10000提高了10倍。這可以自己算一下,就不再寫出來了。
之所以前面寫了這么多,就是因為運放的AoL本身就不是固定的,它跟頻率有關系,這也就造成了運放的使用有了限制。
還是以LM2904為例,手冊表格中的AoL=140V/mV=14萬倍=20log(140000)=102db。手冊還給出了AoL與頻率的關系曲線,如下圖:
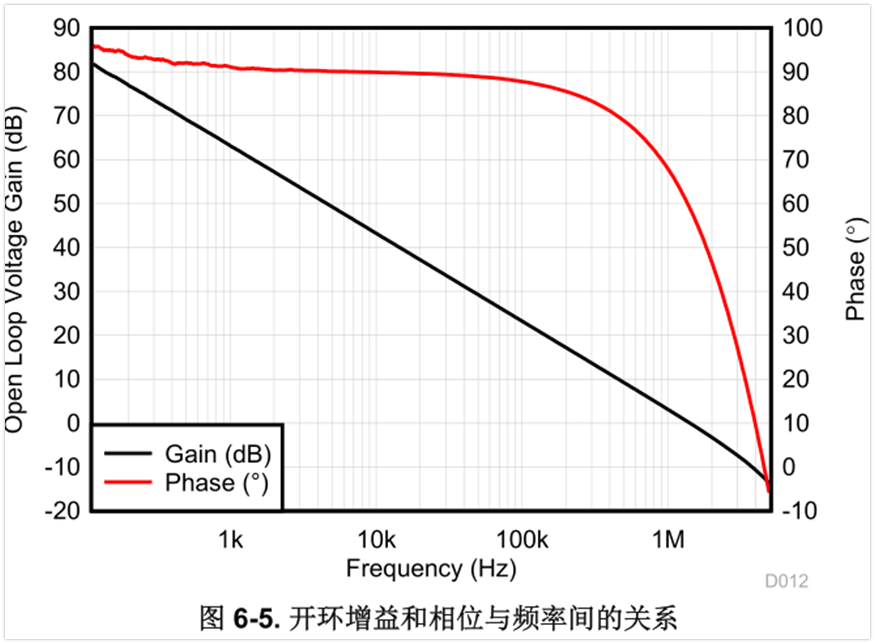
從圖中可以看到,AoL隨頻率是一直在下降的,最左邊的頻率為100Hz,開環增益AoL=82dB左右,相對表格中的直流開環增益AoL=102dB,下降了20dB,也就是10倍。頻率為1Khz的時候,AoL=62dB左右,相對直流AoL下降了40dB,也就是100倍。
極端一點,在1.2Mhz的時候,AoL=0dB,也就是說,這個運放沒有放大作用,開環增益為0,既不放大,也不衰減。這個頻率點也就是運放的單位增益帶寬,也是運放的增益帶寬積。
所以呢,我們在使用運放的時候,我們要看我們放大信號的有效頻率是多大,如果過大,在對應頻率處運放的實際AoL可能就比較小,導致實際增益達不到我們的目標,電路也就失效了。
實際電路如何考慮
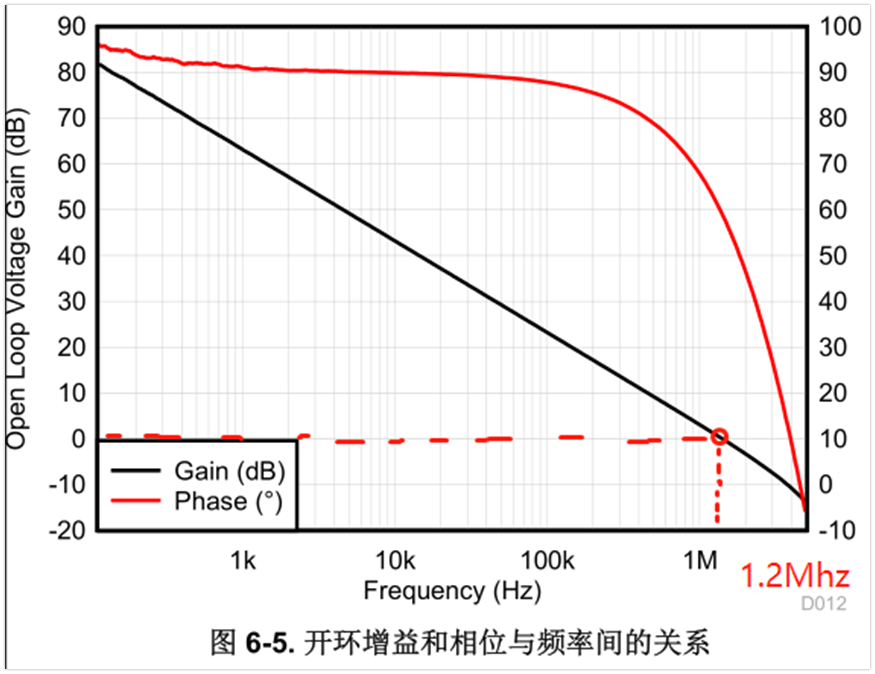
運放基本都給出了一個參數叫增益帶寬積,比如LM2904是1.2Mhz

除此之外,曲線上面也能看出來,對應開環增益為0db的點就是增益帶寬積GBW,也是單位增益帶寬。
前面的章節只是為了說明道理,我們實際設計電路的時候,一般用這個增益帶寬積就夠了。
舉個例子:
問:假設我們要求電路放大10倍,有用信號最大頻率是10Khz,那么這個帶寬積GBW=1.2Mhz的運放能滿足要求嗎?或者說如果要放大10倍,用這個運放最大可以放大多大頻率的信號?
答:
1、f=10Khz,Av=10倍,計算f*Av=100khz < 1.2Mhz,這個運放是可以滿足要求的
2、GBW=1.2Mhz,Av=10倍,計算f=GBW/Av=120Khz,即這個情況下運放最大可以放大120Khz的信號,頻率高了增益就會下降。
需要注意,這個計算本身就是極限值,因為增益帶寬積本身就是3dB時候的,因此此時已經有了一定的衰減,如果完全按照這個計算值來設計,實際得到的增益還是會有所下降的。如果要求特別準確,必須留夠充足的裕量。
上面是通過計算的方法,一些手冊也列舉了閉環增益與頻率的關系,我們也可以看圖,比如下圖是LM2904的曲線。
可以看到,放大10倍的時候,增益下降3db對應的頻率大概就是100K多一點,與前面計算的120Khz基本相符合。如果要求增益非常準確,從曲線上看,頻率可能只能用到30Khz左右了。
小結
關于運放的增益就寫到這里了,主要寫了以下幾點:
1、啥是開環增益,閉環增益
2、開環增益是如何影響閉環增益的
3、電路設計中如何考慮增益與帶寬的問題
審核編輯:湯梓紅
 電子發燒友App
電子發燒友App


















評論