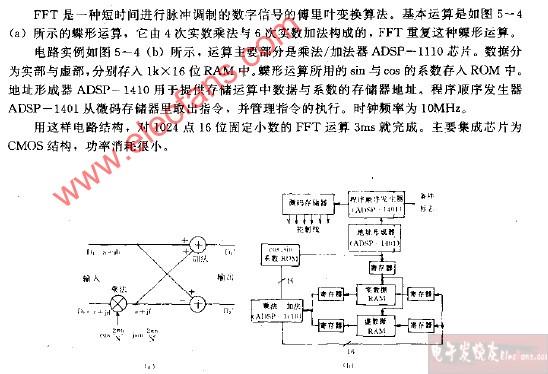
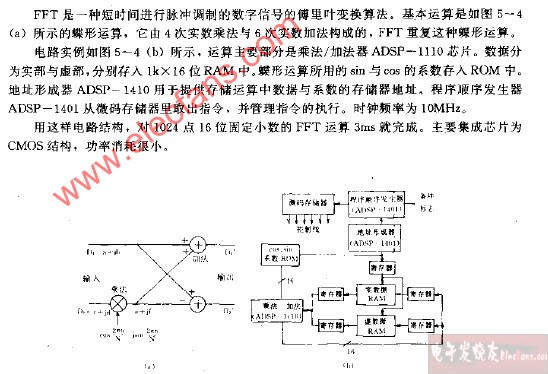
運放電路
由運算放大器組成的電路,簡稱為運放電路。
這些電路可以說是五花八門,是我們學習模擬電子技術的一個重要內容,更是一個電子工程師必須掌握的電路之一。運放電路有多種類型,是不是我們把它們牢牢記住就行了呢?
不是!畢竟電路是會變的,換個套路你如果就不會,這樣就沒有意義了。正確的打開方式還是應該理解它,消化它。
在分析運放電路工作原理時,首先請忘掉什么同向放大、反向放大,什么加法器、減法器,什么差動輸入……暫時忘掉那些輸入輸出關系的公式……這些只會干擾你,讓你更糊涂﹔也請各位暫時不要理會輸入偏置電流、共模抑制比、失調電壓等電路參數,這是設計者要考慮的事情。我們理解的就是理想放大器,因為理解了理想放大器,多數情況是夠用的
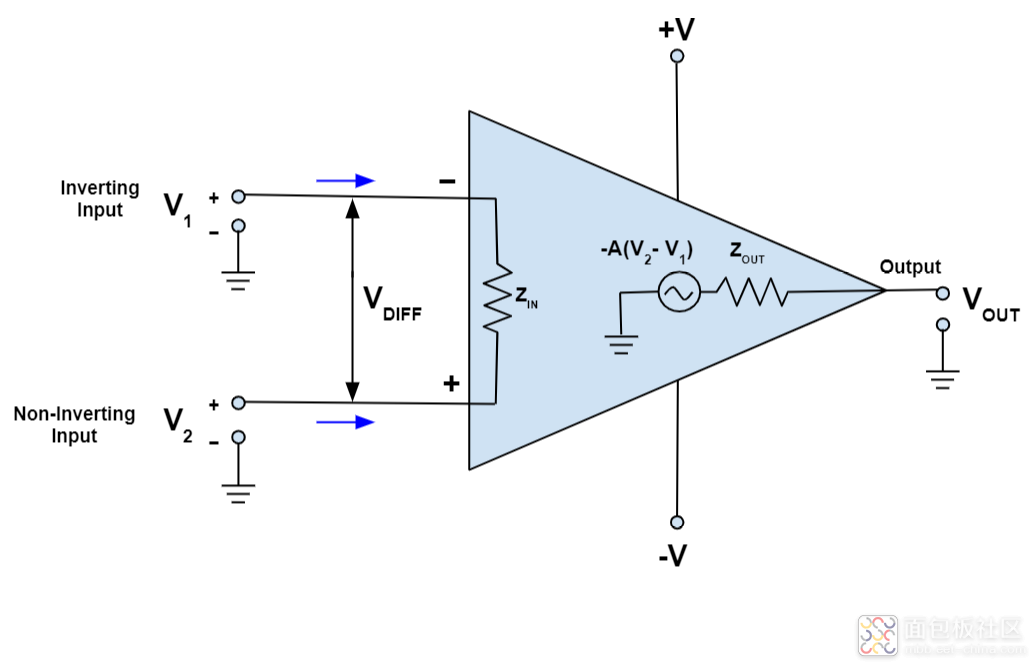
現在,通過兩招就能解決大部分運放問題,并且,這兩招在所有運放電路的教材里都寫得明白,就是“虛短”和“虛斷”,不過要把它運用得出神入化,就要有較深厚的功底了。
基于這一理論,我們通過4個經典電路,來快速掌握運算的分析方法!
關于虛短和虛斷
由于運放的電壓放大倍數很大,一般通用型運算放大器的開環電壓放大倍數都在 80dB 以上。而運放的輸出電壓是有限的,一般在 10 V~14 V。因此運放的差模輸入電壓不足 1 mV,兩輸入端近似等電位,相當于 “短路”。開環電壓放大倍數越大,兩輸入端的電位越接近相等。我們用這樣的反推來理解虛短的概念。
“虛短”是指在分析運算放大器處于線性狀態時,可把兩輸入端視為等電位,這一特性稱為虛假短路,簡稱虛短。顯然不能將兩輸入端真正短路。(輸入差模電壓不大于1mv)
如何理解“虛斷”呢?由于運放的差模輸入電阻很大,一般通用型運算放大器的輸入電阻都在 1MΩ以上。因此流入運放輸入端的電流往往不足 1uA,遠小于輸入端外電路的電流。故通常可把運放的兩輸入端視為開路,且輸入電阻越大,兩輸入端越接近開路。
“虛斷”是指在分析運放處于線性狀態時,可以把兩輸入端視為等效開路,這一特性 稱為虛假開路,簡稱虛斷。顯然不能將兩輸入端真正斷路。(差模輸入電阻無窮大)
好了,概念就介紹到這里,我們來用以上的理論,來分析幾個案例,看是否好使?
第一個案例:
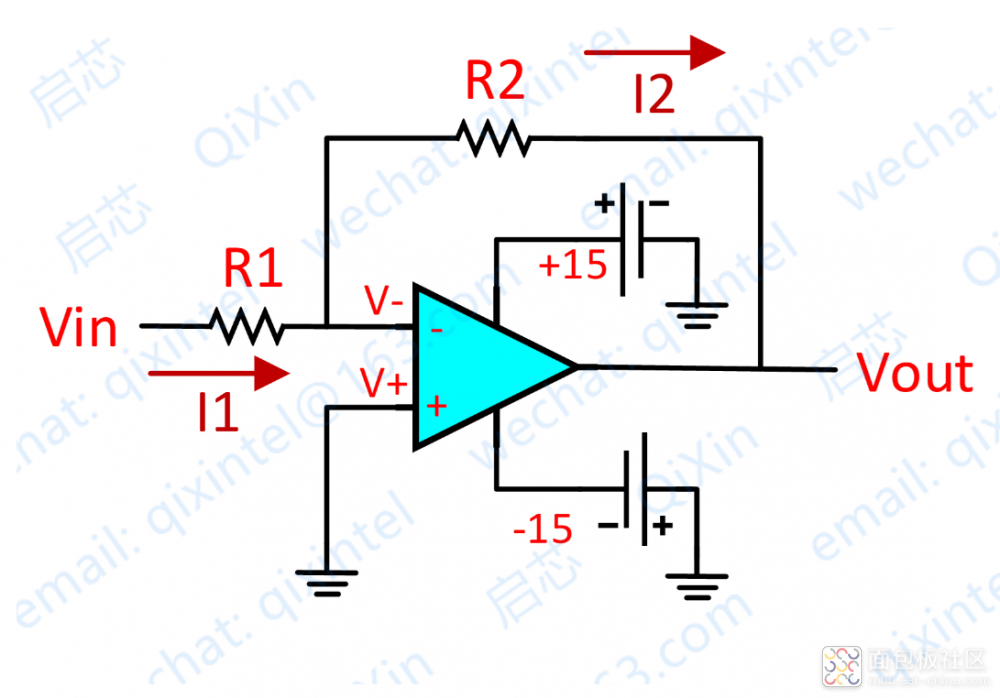
由上圖,分析如下:
首先,根據虛短,圖一運放的同向端接地=0V,反向端和同向端 虛短,所以也是 0V
其次,根據虛斷,反向輸入端輸入電阻很高,虛斷,幾乎沒有電流注入和流出
那么R1和R2相當于是串聯的,流過一個串聯電路中的每一只組件的電流是相同的,即流過 R1 的電流和流過 R2 的電流是相同的。
流過 R1 的電流 I1 = (Vi - V-)/R1
流過 R2 的電流 I2 = (V- - Vout)/R2
V- = V+ = 0
I1 = I2
求解上面的代數方程
Vout = (-R2/R1)*Vi
這樣,我們就設計了一個最經典的反向比例放大器
第二個案例:
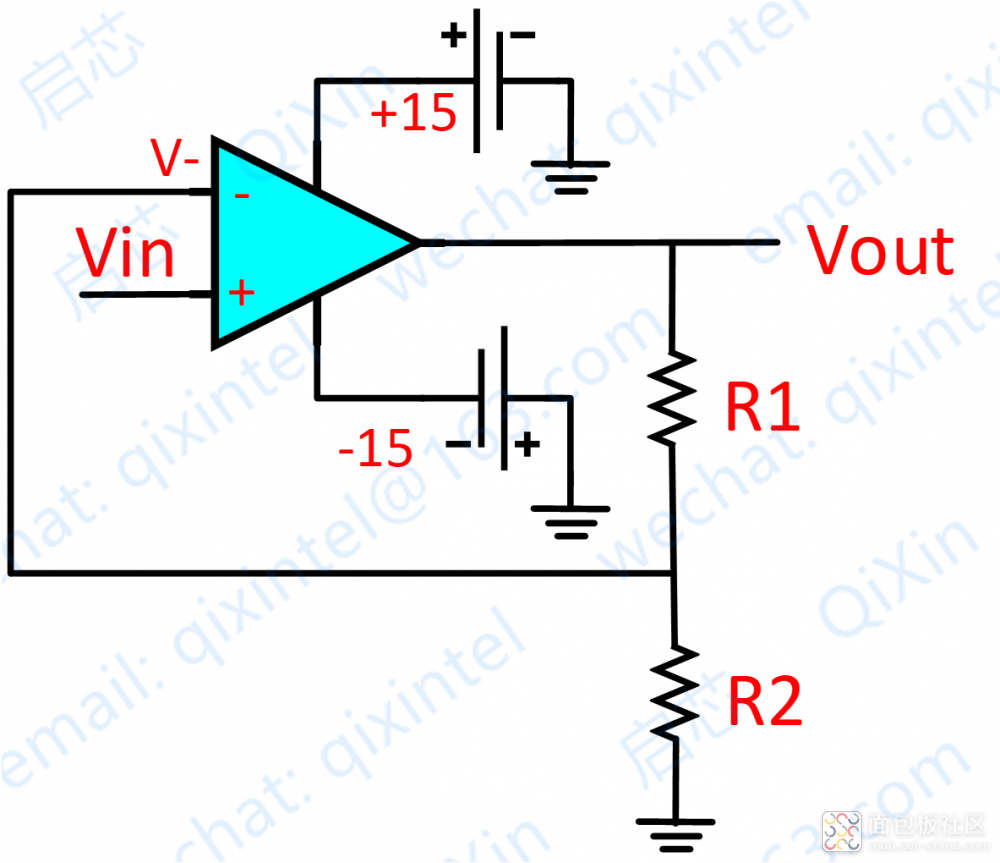
再看上圖,分析如下:
Vi 與 V- 虛短,則 Vi = V-
因為虛斷,反向輸入端沒有電流輸入輸出,通過 R1 和 R2 的電流相等,設此電流為 I
由歐姆定律得:I = Vout/(R1+R2)
Vi 等于 R2 上的分壓, 即:Vi = I*R2
由上面式子得
Vout=Vi*(R1+R2)/R2
這樣,我們就設計了一個同向放大器。
第三個案例:
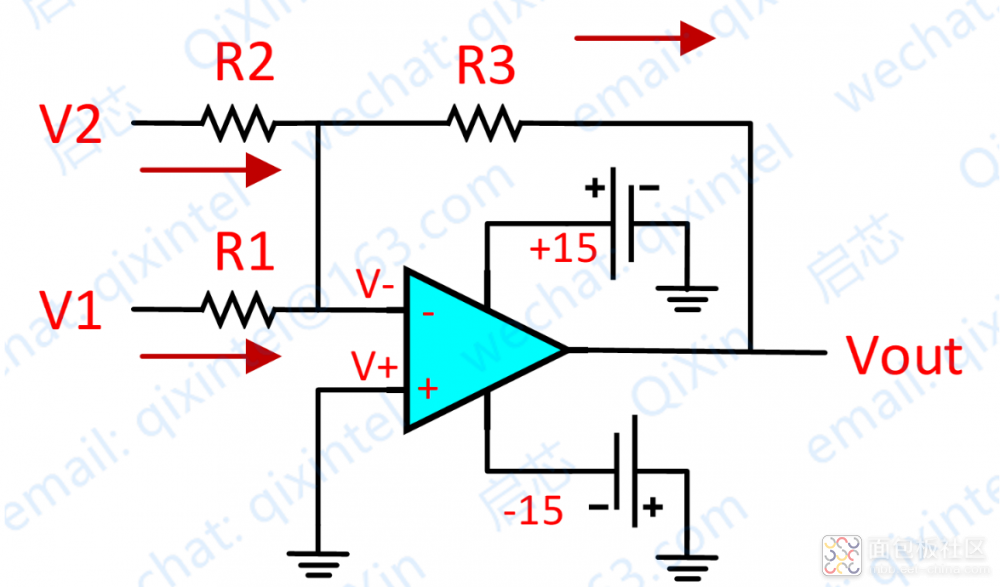
再看上圖,分析如下:
由虛短知:V- = V+ = 0
由虛斷及基爾霍夫定律知,通過 R2 與 R1 的電流之和等于通過 R3 的電流,故 (V1 – V-)/R1 + (V2 – V-)/R2 = (Vout – V-)/R3
聯立上面兩個式子很容易得到 V1/R1 + V2/R2 = Vout/R3
如果存在 R1=R2=R3,則上式變為 Vout=-(V1+V2),
這樣,我們就設計了一個加法器啦。
我一直都認為,實踐是學習的硬件電路知識最好的方法。但是,動手搭建電路很費時間,而設計原理圖打PCB板不僅花時間而且費錢,因此,折衷最好的方法就是仿真了。平心而論,只要模型準確,實際上,仿真的結果是無限接近實際情況的。
況且,通常我們只是工程上設計,判斷趨勢,知道大體方向與數值即可。并不需要太嚴謹的結果,因此,從這個方面來說,仿真大多數情況下,用來分析問題,是完全夠用的。
對于上面這個案例,我們仿真看看,先看簡單的,這個電路和上面的電路唯一不同的是加了平衡電阻
下面是R1=R2=R4的情況,可以看到結果是符合我們預期的,即VO=V1+V2,仿真圖例如下
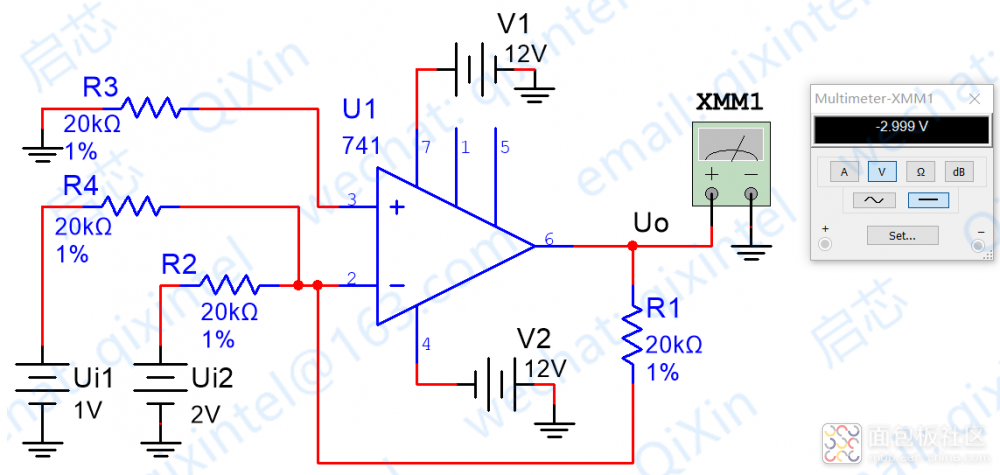
下面是R2=R4 R1=3*R2的情況,可以看到結果也是符合我們預期的,即VO=3*(V1+V2),仿真圖例如下
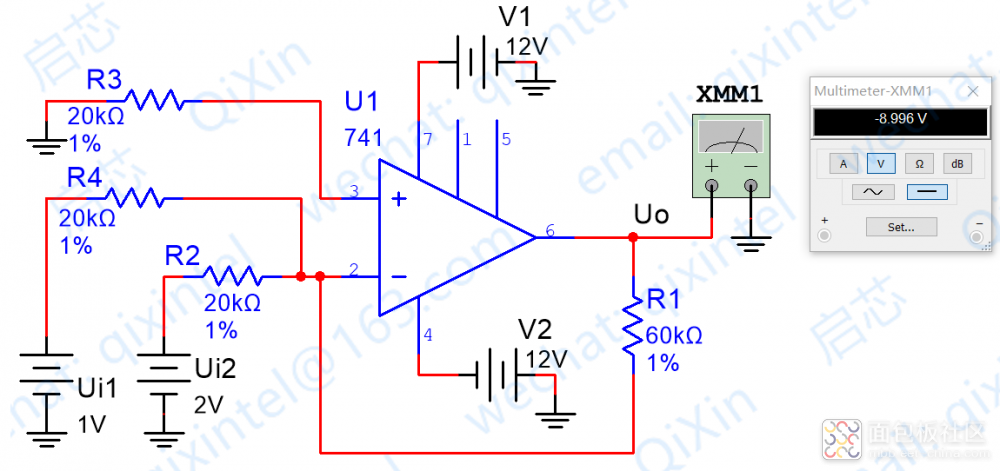
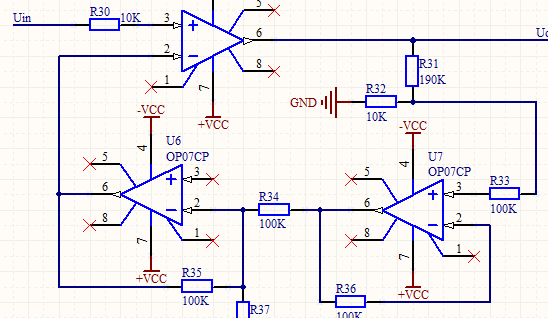
這個電路實際的應用電路,比如用OP07C搭建的低頻噪聲放大電路,如下圖
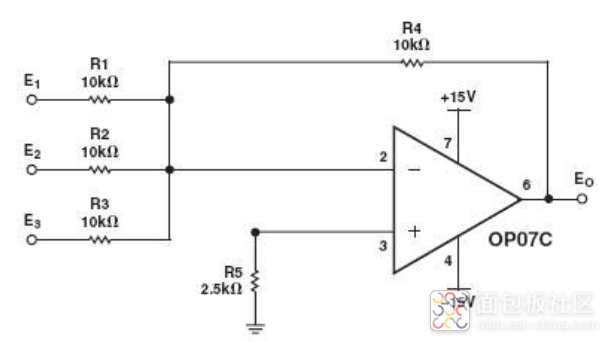
這個電路,比上面講過的電路稍微復雜,但基本的分析原理是一樣的。大家,可以試著計算一下輸出公式。
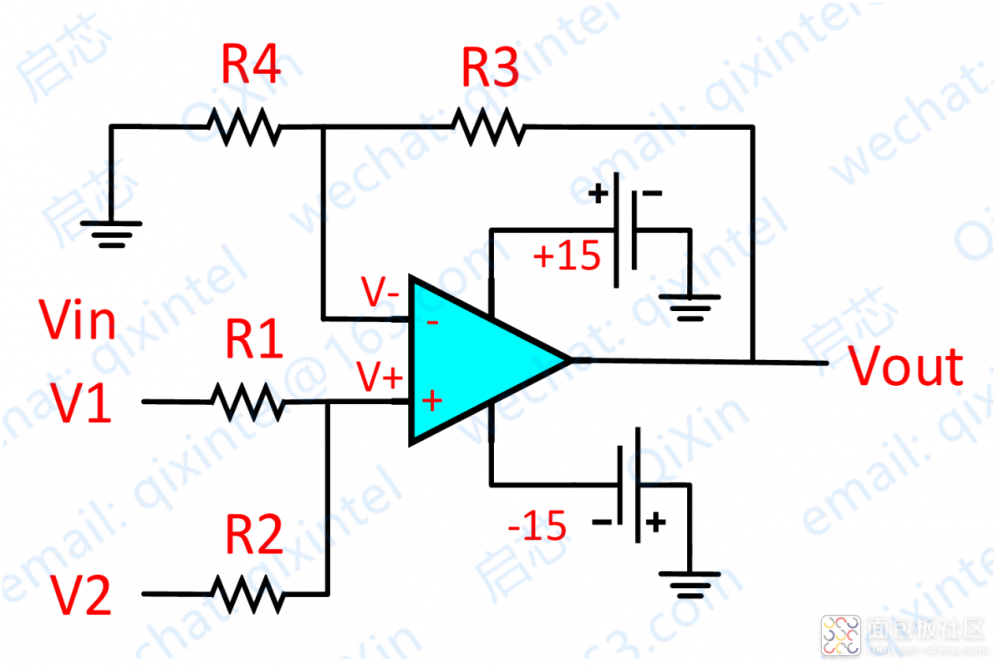
再看上圖,分析如下:
因為虛斷,運放同向端沒有電流流過,則流過 R1 和 R2 的電流相等,同理流過R4和R3的電流也相等。
所以,很容易推出,(V1–V+)/R1 = (V+ - V2)/R2
(Vout – V-)/R3 = V-/R4 ……b
然后,再由虛短知:V+ = V-
如果 存在條件R1=R2,R3=R4,
則由以上式子可以推導出 V+ = (V1 + V2)/2
V- = Vout/2
故 Vout = V1 + V2
這樣,我們就設計了一個新的加法器。
由上面四個例子,我們可以看到基本的運算放大器電路,無論電路的形式、連接如何變化,但只要掌握了基本的原理,虛短和虛斷,運放的電路基本都可以迎刃而解!
?
?
?
?
審核編輯:黃飛
?
 電子發燒友App
電子發燒友App










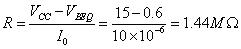










評論