被喻為“重要數(shù)據(jù)保險(xiǎn)箱”的安全芯片已經(jīng)滲入人們生活的方方面面。隨著5G、物聯(lián)網(wǎng)、車聯(lián)網(wǎng)的迅速發(fā)展，為安全芯片開啟了新的應(yīng)用場(chǎng)景，同時(shí)也帶來(lái)了新的挑戰(zhàn)。

本文將帶大家深入了解安全芯片的核心，后量子密碼認(rèn)證技術(shù)。

1、安全認(rèn)證技術(shù)概述

安全認(rèn)證技術(shù)是防止信息被篡改、刪除、重放和偽造的一種有效方法。它使接收者能夠識(shí)別和確認(rèn)消息的來(lái)源和真?zhèn)巍Ｄ壳罢J(rèn)證技術(shù)主要有4種：

（1）數(shù)字摘要

（2）數(shù)字摘要+對(duì)稱密鑰認(rèn)證

（3）數(shù)字摘要+非對(duì)稱密鑰認(rèn)證

（4）數(shù)字證書認(rèn)證

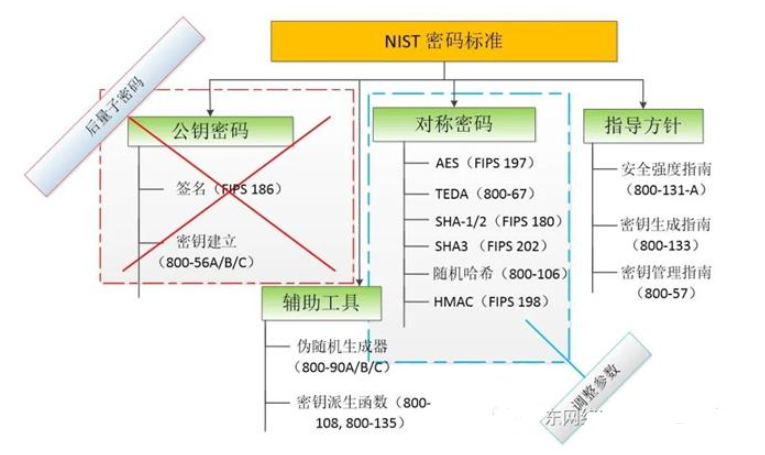
不過(guò)隨著量子計(jì)算機(jī)的發(fā)展，現(xiàn)有的絕大多數(shù)公鑰密碼算法（RSA、Diffie-Hellman、橢圓曲線等）能被足夠大和穩(wěn)定的量子計(jì)算機(jī)攻破，也就是說(shuō)目前基于非對(duì)稱密鑰的認(rèn)證技術(shù)都不安全，會(huì)被攻破。所以需要研究基于后量子密碼的認(rèn)證技術(shù)。

1.1 數(shù)字摘要

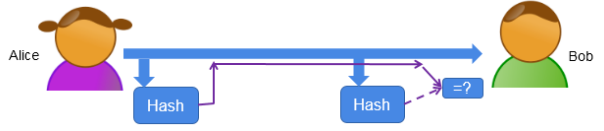
該技術(shù)就是使用單向的HASH函數(shù)將需發(fā)送的消息摘要成為一串固定長(zhǎng)度的數(shù)據(jù)，然后發(fā)送給接收方。

具體步驟如下：

（1）使用Hash函數(shù)計(jì)算消息的摘要，將其與消息一起發(fā)送。

（2）當(dāng)Bob收到消息，使用同樣算法計(jì)算摘要，與收到的摘要進(jìn)行比較。

主要優(yōu)點(diǎn)：

（1）對(duì)消息的任何改變，摘要必然變化。

（2）單向函數(shù)：無(wú)法從摘要構(gòu)造出原文。

主要缺點(diǎn)：

（1）僅僅Hash沒(méi)法保證完整性。

（2）改變這個(gè)消息，重新計(jì)算摘要，用改變后的消息+摘要替換原來(lái)的報(bào)文。

1.2 數(shù)字摘要+對(duì)稱密鑰認(rèn)證

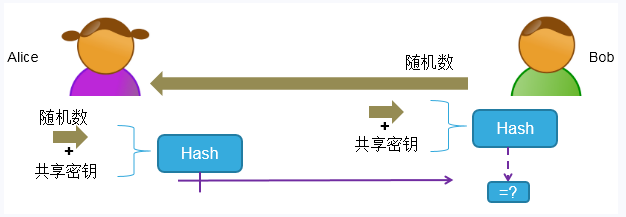
該技術(shù)就是使用共享的對(duì)稱密鑰加密隨機(jī)數(shù)，再使用HASH函數(shù)將密文信息摘要成為一串固定長(zhǎng)度的數(shù)據(jù)，然后發(fā)送給接收方。

具體步驟如下：

（1）通過(guò)安全通道，Bob和Alice共享一個(gè)密鑰。

（2）Bob發(fā)送一個(gè)隨機(jī)數(shù)給Alice。

（3）Alice用共享密鑰加密隨機(jī)數(shù)，并對(duì)加密結(jié)果進(jìn)行HASH運(yùn)算，HASH值發(fā)送給Bob。

（4）Bob也用共享密鑰加密隨機(jī)數(shù)，并對(duì)加密結(jié)果進(jìn)行HASH運(yùn)算，計(jì)算的結(jié)果與接收的HASH進(jìn)行比較，相等則表示是Alice發(fā)送過(guò)來(lái)的。

主要優(yōu)點(diǎn)：

（1）在確保密鑰安全下，可以防止信息被篡改。

（2）分組加密性能快。

主要缺點(diǎn)：

（1）需要通過(guò)安全通道共享密鑰。

（2）雙方都保存密鑰，只要一方泄漏密鑰即可破解信息。

1.3 數(shù)字摘要+非對(duì)稱密鑰認(rèn)證

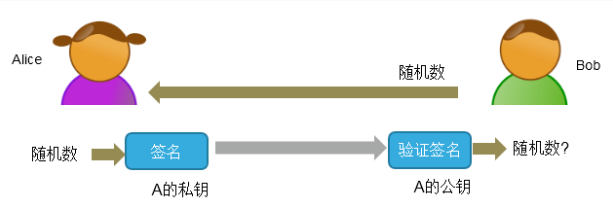
該技術(shù)就是使用自己的私鑰對(duì)發(fā)送信息進(jìn)行簽名，然后接收方使用公鑰驗(yàn)證這個(gè)簽名。

具體步驟如下：

（1）Bob拿到Alice的公鑰，發(fā)送一個(gè)隨機(jī)數(shù)給Alice。

（2）Alice收到隨機(jī)數(shù)后用自己的私鑰進(jìn)去簽名，簽名結(jié)果發(fā)送給Bob。

（3）Bob使用Alice的公鑰對(duì)接收的簽名進(jìn)行驗(yàn)簽，如果驗(yàn)簽通過(guò)則確認(rèn)是Alice發(fā)出來(lái)的信息。

主要優(yōu)點(diǎn)：

（1）公鑰可以公開，無(wú)需保密。

（2）只需發(fā)送方保存自己的私鑰。

主要缺點(diǎn)：

（1）如何確定公鑰來(lái)自Alice？易受中間人攻擊。

1.4 數(shù)字證書認(rèn)證

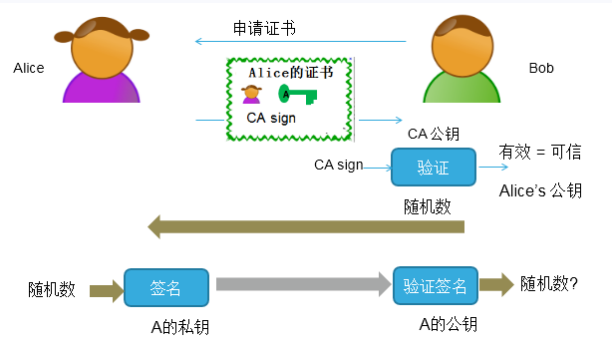
該技術(shù)就是需要有一個(gè)CA（可信的授權(quán)中心），發(fā)送方Alice從CA申請(qǐng)證書，CA確認(rèn)Alice確實(shí)是Alice，生成和發(fā)布Alice的證書。Alice的證書包含：

· 主題Subject：需要鑒別的個(gè)人Alice

· Alice的公鑰public key

· 數(shù)字簽名digital signature：CA對(duì)證書的簽名

· 發(fā)布者Issuer：驗(yàn)證了信息并發(fā)布證書的實(shí)體

· 簽名算法Signature Algorithm

具體步驟如下：

（1）Bob申請(qǐng)Alice的證書公鑰。

（2）Alice把自己的證書發(fā)送給Bob，Bob收到后使用CA公鑰驗(yàn)證證書，并獲取得到Alice的公鑰。

（3）Bob拿到Alice的公鑰后，發(fā)送一個(gè)隨機(jī)數(shù)給Alice。

（4）Alice收到隨機(jī)數(shù)后用自己的私鑰進(jìn)去簽名，簽名結(jié)果發(fā)送給Bob。

（5）Bob使用Alice的公鑰對(duì)接收的簽名進(jìn)行驗(yàn)簽，如果驗(yàn)簽通過(guò)則確認(rèn)是Alice發(fā)出來(lái)的信息。

主要優(yōu)點(diǎn)：

（1）可以抵抗中間人攻擊，確認(rèn)Alice的公鑰。

主要缺點(diǎn)：

（1）無(wú)法抵抗量子計(jì)算機(jī)攻擊。

2、后量子密碼算法概述

后量子密碼是能夠抵抗量子計(jì)算機(jī)對(duì)現(xiàn)有密碼算法攻擊的新一代密碼算法。實(shí)現(xiàn)后量子密碼算法主要有以下 4 種途徑 ：

（1）基于哈希 （Hash-based）：最早出現(xiàn)于1979 年，主要用于構(gòu)造數(shù)字簽名。代表算法：Merkle 哈希樹簽名、XMSS、Lamport 簽名等。

（2）基于編碼 （Code-based）：最早出現(xiàn)于1978 年，主要用于構(gòu)造加密算法，代表算法：McEliece。

（3）基于多變量（Multivariate-based）：最早出現(xiàn)于1988年，主要用于構(gòu)造數(shù)字簽名、加密、密鑰交換等。代表方法/算法：HFE （Hidden Field Equations）、Rainbow （Unbalanced Oil and Vinegar （UOV） 方法）、HFEv- 等。

（4）基于格（Lattice-based）：最早出現(xiàn)于1996 年，主要用于構(gòu)造加密、數(shù)字簽名、密鑰交換，以及眾多高級(jí)密碼學(xué)應(yīng)用，如：屬性加密 （Attribute-based encryption）、陷門函數(shù) （Trapdoor functions）、偽隨機(jī)函數(shù) （Pseudorandom functions）、同態(tài)加密 （Homomorphic Encryption） 等。代表算法：NTRU 系列、NewHope （Google 測(cè)試過(guò)的）、一系列同態(tài)加密算法 （BGV、GSW、FV 等）。由于其計(jì)算速度快、通信開銷較小，且能被用于構(gòu)造各類密碼學(xué)算法和應(yīng)用，因此被認(rèn)為是最有希望的后量子密碼技術(shù)。

當(dāng)參數(shù)選取適當(dāng)時(shí)，目前沒(méi)有已知的經(jīng)典和量子算法可以快速求解這些問(wèn)題。

再次強(qiáng)調(diào)，這些算法的安全性，依賴于有沒(méi)有可以快速求解其底層數(shù)學(xué)問(wèn)題或直接對(duì)算法本身的高效攻擊算法。這也正是量子計(jì)算機(jī)對(duì)于公鑰密碼算法有很大威脅的原因。

除這4種問(wèn)題之外，還有基于超奇異橢圓曲線 （Supersingular elliptic curve isogeny）、量子隨機(jī)漫步 （Quantum walk） 等技術(shù)的后量子密碼構(gòu)造方法。另外，對(duì)稱密碼算法在密鑰長(zhǎng)度較大時(shí) （例如 AES-256），也可被認(rèn)為是后量子安全的。

為什么上面列的 4 種是最重要的？因?yàn)檫@ 4 類途徑是最能構(gòu)造出公鑰密碼學(xué)中已有的各類算法的后量子版本，甚至還能超越（例如基于格的（全）同態(tài)加密）等。

1.1 基于哈希 （Hash-based）

基于哈希的簽名算法由 Ralph Merkel 提出，被認(rèn)為是傳統(tǒng)數(shù)字簽名 （RSA、DSA、ECDSA 等 ） 的可行代替算法之一。基于哈希的簽名算法由一次性簽名方案演變而來(lái)，并使用 Merkle 的哈希樹認(rèn)證機(jī)制。哈希樹的根是公鑰，一次性的認(rèn)證密鑰是樹中的葉子節(jié)點(diǎn)。基于哈希的簽名算法的安全性依賴哈希函數(shù)的抗碰撞性。由于沒(méi)有有效的量子算法能快速找到哈希函數(shù)的碰撞，因此（輸出長(zhǎng)度足夠長(zhǎng)的）基于哈希的構(gòu)造可以抵抗量子計(jì)算機(jī)攻擊。此外，基于哈希的數(shù)字簽名算法的安全性不依賴某一個(gè)特定的哈希函數(shù)。即使目前使用的某些哈希函數(shù)被攻破，則可以用更安全的哈希函數(shù)直接代替被攻破的哈希函數(shù)。

1.2 基于編碼 （Code-based）

基于編碼的算法使用錯(cuò)誤糾正碼對(duì)加入的隨機(jī)性錯(cuò)誤進(jìn)行糾正和計(jì)算。一個(gè)著名的基于編碼的加密算法是 McEliece 。McEliece使用隨機(jī)二進(jìn)制的不可約 Goppa碼作為私鑰，公鑰是對(duì)私鑰進(jìn)行變換后的一般線性碼。Courtois、Finiasz 和Sendrier 使用 Niederreiter 公鑰加密算法構(gòu)造了基于編碼的簽名方案。基于編碼的算法（例如 McEliece）的主要問(wèn)題是公鑰尺寸過(guò)大。基于編碼的算法包括加密、密鑰交換等。

1.3 基于多變量 （Multivariate-based）

基于多變量的算法使用有限域上具有多個(gè)變量的二次多項(xiàng)式組構(gòu)造加密、簽名、密鑰交換等算法 。多變量密碼的安全性依賴于求解非線性方程組的困難程度，即多變量二次多項(xiàng)式問(wèn)題。該問(wèn)題被證明為非確定性多項(xiàng)式時(shí)間困難。目前沒(méi)有已知的經(jīng)典和量子算法可以快速求解有限域上的多變量方程組。與經(jīng)典的基于數(shù)論問(wèn)題的密碼算法相比，基于多變量的算法的計(jì)算速度快，但公鑰尺寸較大，因此適用于無(wú)需頻繁進(jìn)行公鑰傳輸?shù)膽?yīng)用場(chǎng)景，例如物聯(lián)網(wǎng)設(shè)備等。

1.4 基于格 （Lattice-based）

基于格的算法由于在安全性、公私鑰尺寸、計(jì)算速度上達(dá)到了更好的平衡，被認(rèn)為是最有前景的后量子密碼算法之一。與基于數(shù)論問(wèn)題的密碼算法構(gòu)造相比，基于格的算法可以實(shí)現(xiàn)明顯提升的計(jì)算速度、更高的安全強(qiáng)度和略微增加的通信開銷。與其他幾種實(shí)現(xiàn)后量子密碼的方式相比，格密碼的公私鑰尺寸更小，并且安全性和計(jì)算速度等指標(biāo)更優(yōu)。此外，基于格的算法可以實(shí)現(xiàn)加密、數(shù)字簽名、密鑰交換、屬性加密、函數(shù)加密、全同態(tài)加密等各類現(xiàn)有的密碼學(xué)構(gòu)造。基于格的算法的安全性依賴于求解格中問(wèn)題的困難性。

在達(dá)到相同（甚至更高）的安全強(qiáng)度時(shí)，基于格的算法的公私鑰尺寸比上述三種構(gòu)造更小，計(jì)算速度也更快，且能被用于構(gòu)造多種密碼學(xué)原語(yǔ)，因此更適用于真實(shí)世界中的應(yīng)用。近年來(lái)，基于LWE （Learning with Errors） 問(wèn)題 和 RLWE （Ring-LWE） 問(wèn)題的格密碼學(xué)構(gòu)造發(fā)展迅速，被認(rèn)為是最有希望被標(biāo)準(zhǔn)化的技術(shù)路線之一。

3、格密碼算法概述

格（lattice）是一種數(shù)學(xué)結(jié)構(gòu)，定義為一組線性無(wú)關(guān)的非0向量（稱作格基）的整系數(shù)線性組合。具體來(lái)說(shuō)，給定一組格基X1，。..。..，Xn對(duì)任意的整數(shù)C1，。..，Cn，C1X1+.。.+CnXn都是屬于這個(gè)格的向量，n稱為格的維數(shù)。例如，下圖表示了一個(gè)二維格和兩組不同的格基：X1

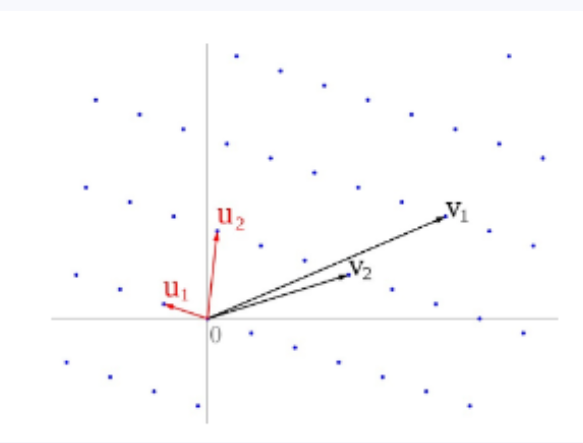
一個(gè)格的格基可以不是唯一的，例如，（（2，1），（1，1））和（（1，0），（0，1））都是二維整數(shù)格的一組格基。從上圖中可以看到，即使是定義了同樣的格的兩組格基，其長(zhǎng)度也可能相差很大。數(shù)學(xué)家和密碼學(xué)家們普遍認(rèn)為，對(duì)于一個(gè)維數(shù)足夠高的格，通過(guò)一組隨機(jī)選取的格基找到一組短格基，或得到一組線性無(wú)關(guān)的短格向量是困難的。這個(gè)問(wèn)題稱作最短獨(dú)立向量問(wèn)題（SIVP）。除此之外，還有一些其他的基于格的困難問(wèn)題，如gap-SVP、BDD等。以上的困難問(wèn)題通常屬于數(shù)學(xué)上的理論研究范疇。在密碼學(xué)的實(shí)際應(yīng)用當(dāng)中，格密碼算法所基于的困難問(wèn)題更多采用容錯(cuò)學(xué)習(xí)（LWE）問(wèn)題。

LWE問(wèn)題這樣表述：給定隨機(jī)矩陣A和向量As+e mod q，其中e是小的誤差項(xiàng)，q是模數(shù)（通常取較大的素?cái)?shù)），從中恢復(fù)隨機(jī)的s是困難的。我們稱（A，b=As+e mod q）為L(zhǎng)WE樣本，s為L(zhǎng)WE秘密。容易看到，如果不存在誤差項(xiàng)e，這一問(wèn)題即為求解線性方程組，是易解的。然而，當(dāng)引入誤差e之后，LWE問(wèn)題可歸約到SIVP等格上的困難問(wèn)題，即求解LWE問(wèn)題的難度不低于求解格上的困難問(wèn)題。

在應(yīng)用于密碼算法時(shí)，LWE問(wèn)題存在一個(gè)很大的優(yōu)勢(shì)：存在“最壞情況到平均情況的歸約”，即求解平均情況下的LWE問(wèn)題，其難度不低于最難的SIVP問(wèn)題實(shí)例。在一些早期的公鑰密碼算法，如基于背包問(wèn)題的密碼體制中，由于存在一些易解的背包問(wèn)題實(shí)例，使得當(dāng)參數(shù)選取不恰當(dāng)時(shí)，密碼算法的安全性易受攻擊。而對(duì)于基于LWE問(wèn)題的格密碼來(lái)說(shuō)，由于存在最壞情況到平均情況的歸約，因而可以避免這種攻擊的產(chǎn)生。這為基于LWE問(wèn)題設(shè)計(jì)的密碼算法帶來(lái)了很大安全性上的優(yōu)勢(shì)。

直接通過(guò)LWE問(wèn)題構(gòu)造的密碼學(xué)方案效率并不是很高。更多的時(shí)候，我們將整數(shù)向量用多項(xiàng)式代替，得到多項(xiàng)式LWE或稱環(huán)LWE。一個(gè)環(huán)LWE樣本為（a，b=as+e mod q），其中a，s，e 均為多項(xiàng)式。環(huán)LWE的安全性建立在理想格中相應(yīng)數(shù)學(xué)問(wèn)題困難性的基礎(chǔ)之上。盡管這些問(wèn)題在困難性上面被認(rèn)為不如格問(wèn)題更可靠，但目前還沒(méi)有發(fā)現(xiàn)可以有效求解這些問(wèn)題的算法。此外，還有可靠性介于LWE和環(huán)LWE問(wèn)題之間的模LWE問(wèn)題，以及這些問(wèn)題的變種LWR、環(huán)LWR、模LWR問(wèn)題。格密碼的安全性基本上都依賴于這些問(wèn)題的困難性。

1.1 基于格的公鑰加密算法

通常，在一個(gè)基于LWE問(wèn)題設(shè)計(jì)的密碼算法中，我們將LWE樣本作為公鑰使用，而將LWE秘密作為私鑰使用，這保證了公鑰不會(huì)泄露關(guān)于私鑰的信息。我們令公鑰為 （a，b=as+e mod q），私鑰為 s ，這里 a，b，s，e均為多項(xiàng)式，且s，e的系數(shù)相比于q是較小的（理論上s和e的系數(shù)應(yīng)取為離散正態(tài)分布，但在實(shí)際應(yīng)用中，出于實(shí)現(xiàn)上的效率和安全，s和e通常使用二項(xiàng)分布或均勻分布來(lái)模擬）。我們下面描述最基礎(chǔ)的格公鑰加密方案。

對(duì)于需要加密的消息，我們將消息記為 0-1 系數(shù)的多項(xiàng)式 m 。

（1）首先隨機(jī)選取系數(shù)較小的多項(xiàng)式 r，e1，e2

（2）計(jì)算密文c=ar+e1 mod q和 d=br+e2+m（q-1）/2 mod q

容易看到，由于 as≈b mod q，故ars≈br mod q，且 （ar+e1）s≈br+e2 mod q。當(dāng)s，e，r，e1，e2均足夠小時(shí)，可以保證br+e2-（ar+e1）s mod q的系數(shù)均不超過(guò)（q-1）/4。故d-cs和m（q-1）/2的每個(gè)系數(shù)之差都不超過(guò)（q-1）/4。我們可以通過(guò)這樣的方式從d-cs中還原m;若d-cs的第i個(gè)系數(shù)距離0更近，則令m的第i位為0；若 d-cs的第i位系數(shù)距離（q-1）/2更近，則令m的第i位系數(shù)為1。這樣我們成功通過(guò)私鑰s解密了密文（c，d），得到消息m。這一算法的安全性由兩個(gè)部分保證：其一是私鑰的安全性，由于公鑰為L(zhǎng)WE樣本，通過(guò)公鑰不會(huì)泄露私鑰的信息；其二是消息的安全性，由于密文同樣為L(zhǎng)WE樣本，通過(guò)密文在未知私鑰的前提下，不會(huì)泄露消息。以上描述的簡(jiǎn)單方案是選擇明文安全，而非選擇密文安全的。對(duì)于具體的方案，則需要應(yīng)用密碼學(xué)中著名的Fujisaka-Okamoto變換，將以上的基礎(chǔ)方案轉(zhuǎn)變?yōu)檫x擇密文安全的方案。

1.2 基于格的數(shù)字簽名算法

對(duì)于RSA、橢圓曲線等密碼體制來(lái)說(shuō)，其中的公鑰加密和數(shù)字簽名算法存在一定的對(duì)偶性：可通過(guò)簡(jiǎn)單的交換公私鑰，將公鑰加密算法轉(zhuǎn)化為數(shù)字簽名算法。

然而，對(duì)于格密碼而言，這種對(duì)偶性并不存在，這意味著我們需要通過(guò)新的方式構(gòu)造數(shù)字簽名算法。被密碼學(xué)家廣泛采用的一種方式，即通過(guò)零知識(shí)證明協(xié)議構(gòu)造數(shù)字簽名。零知識(shí)證明可能是密碼學(xué)中最為神奇的一類應(yīng)用。零知識(shí)證明解決這樣一個(gè)問(wèn)題：我們是否可以向他人提供對(duì)一個(gè)命題的證明，但卻不泄露證明這一命題所需要的知識(shí)？盡管看起來(lái)有些反直覺(jué)，但這一點(diǎn)事實(shí)上是可以做到的。實(shí)現(xiàn)安全的數(shù)字簽名，最基本的需求是令驗(yàn)證者有能力對(duì)簽名者的身份進(jìn)行認(rèn)證。而這等價(jià)于這樣的一個(gè)零知識(shí)證明：證明者可證明自己擁有（和對(duì)應(yīng)身份的公鑰匹配的）私鑰，但不向驗(yàn)證者泄露關(guān)于私鑰的信息。這是一類最簡(jiǎn)單的零知識(shí)證明協(xié)議，通常稱為∑協(xié)議。

∑協(xié)議由以下三個(gè)步驟構(gòu)成：

（1）證明者給出承諾w。證明者首先隨機(jī)選擇y，并通過(guò)y生成承諾w，交給驗(yàn)證者。

（2）驗(yàn)證者提出挑戰(zhàn) c。驗(yàn)證者給出均勻隨機(jī)的挑戰(zhàn)c。

（3）證明者給出應(yīng)答z。證明者通過(guò)第一步中的y、挑戰(zhàn)c以及用戶私鑰，得到應(yīng)答 z。（我們額外要求z在其值域上是均勻隨機(jī)的）驗(yàn)證者可通過(guò)用戶公鑰、挑戰(zhàn)c以及承諾w確認(rèn)z是否是由證明者合法生成的。

我們將（w，c，z）三元組稱為協(xié)議的抄本（transcript）。在具備零知識(shí)性的 ∑ 協(xié)議中，我們通常要求在未知私鑰的情況下（1） 通過(guò)w和c得到z是困難的；（2） 通過(guò)c和z得到w是容易的。因此，即使在未知私鑰的前提下，（w，c，z）三元組也可以通過(guò)這樣的方式生成：首先隨機(jī)選取c和z，然后得到w。由于這一生成方式不需要私鑰的參與，故協(xié)議的抄本不包含關(guān)于私鑰的任何知識(shí)！這就保證了協(xié)議的零知識(shí)性。

由于∑協(xié)議需要證明者和驗(yàn)證者之間實(shí)施交互，故無(wú)法直接應(yīng)用于構(gòu)造數(shù)字簽名。但注意到∑協(xié)議要求挑戰(zhàn)c均勻隨機(jī)選取，而正如我們所知，一個(gè)安全的哈希函數(shù)，其輸出和隨機(jī)值是不可區(qū)分的。因此，我們可以將承諾w和需要簽名的消息m輸入哈希函數(shù)H，并用哈希函數(shù)的輸出模擬挑戰(zhàn) c，從而不需要額外的驗(yàn)證者提出挑戰(zhàn)。與此同時(shí)，由于有簽名消息的參與，也實(shí)現(xiàn)了消息和∑協(xié)議抄本的綁定。這個(gè)方法稱為Fiat-Shamir變換。可以證明，安全的∑協(xié)議通過(guò)Fiat-Shamir變換，得到安全的數(shù)字簽名方案。

下面我們簡(jiǎn)單介紹如何基于LWE問(wèn)題構(gòu)造∑協(xié)議，進(jìn)而構(gòu)造數(shù)字簽名。和公鑰加密算法類似，我們令公鑰為 （a，b=as+e mod q），私鑰為 s 。

（1）首先隨機(jī)選取較小的y

（2）令承諾w為ay的高比特位，以排除誤差項(xiàng)的影響

（3）對(duì)于挑戰(zhàn)c，令應(yīng)答z = y + cs。（注意到我們要求z均勻隨機(jī)，故需要排除一些令z不隨機(jī)的邊緣取值：當(dāng)z為邊緣取值時(shí)，需要重新選取y并再次計(jì)算z。我們這里不展開細(xì)節(jié)）

由于ay = az – cas ≈ az – cb mod q，故只需驗(yàn)證w 是否為 az–cb的高比特位即可。對(duì)于需要簽名的消息m和雜湊函數(shù)H，我們令c = H（w||m），即可將這一協(xié)議轉(zhuǎn)化為簽名算法（在驗(yàn)簽時(shí)需要驗(yàn)證c = H（w||m））。