0引言
??? 數字信號處理器(DSP)已經被廣泛應用于通信,智能控制,運動控制等許多領域中。由于具有處理速度快、靈活、精確、可靠等特點,DSP已逐漸取代了傳統的模擬控制,例如開關電源中的DC/DC變換器,PFC變換器,以及高頻脈寬調制(PWM)逆變器等[1][2]。而在這些應用中,為了消除高頻噪聲的影響,也同時為了增加功率密度,通常要求開關頻率保持在20kHz以上。如不考慮采樣保持時間和模/數轉換,一般的DSP芯片都能夠在此頻率以上工作。但這些應用場合又必須對模擬電壓和電流進行采樣,才能保證反饋控制的有效性。本文在傳統PFC變換器控制電路的基礎上,提出了一種采用DSP作為PFC的控制電路的方法,并詳細分析了在平均電流模式控制下傳統的單周期單采樣(SSOP)的方法,最后提出了能夠大大改善開關抗噪聲性能的新穎采樣算法。
1??? 基于DSP的PFC控制策略原理
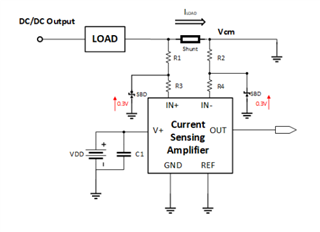
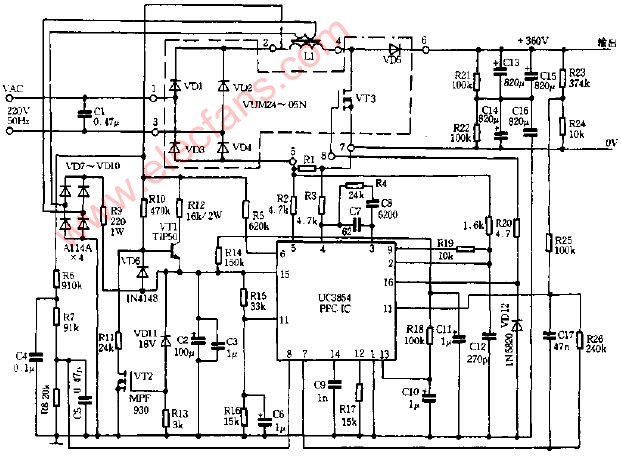
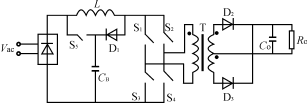
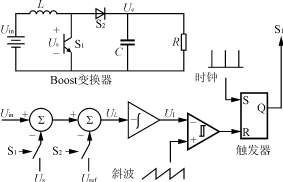
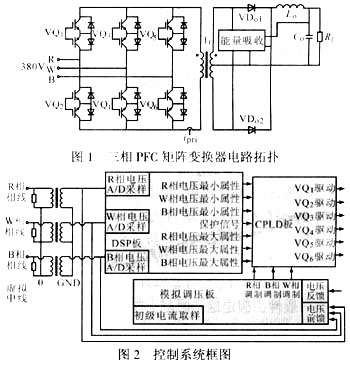
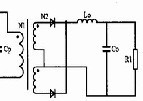
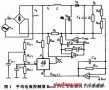
??? 圖1所示為PFC變換器的系統框圖和DSP控制。為了獲得高功率因數,采用了升壓拓撲結構。乘法器是圖中的關鍵部件,其輸入信號為電壓環路中電壓補償器EA1的輸出電壓信號和整流電壓|Vin|信號,其輸出作為控制開關管的基準,與反映電感電流IL的信號進行比較,從而控制開關管的通斷時間。因此,變換器必須同時對輸入電流Iin,輸入電壓Vin和輸出電壓Vout采樣。
??? 為了實現PFC變換器的數字控制,要求轉移函數為離散表達式。為方便起見,這里首先采用拉普拉斯變換。電壓補償器EA1的連續轉移函數可表示為
??? G1(s)=(Vref-Vp)/(Vv-sam-Vref)=K1+K2/s(1)
式中:K1=Rvf/Rvi;K2=1/RviCvf。
??? 考慮到第一級采樣和保持效果,將式(1)變成式(2),即
??? G1′(s)=G1(s)=
(2)
式中:T為開關周期。
??? 從而得到轉移函數的離散表達式如式(3)所示。
??? ΔVo(k)=ΔVo(k-1)+K1ΔVI(k)+(TK2-K1)ΔVI(k-1)(3)
式中:ΔVo(k)=Vref-Vp(k);
??????????? ΔVI(k)=Vv-sam(k)-Vref;
????? k為采樣序列數。
??? 從式(3)中可以清楚地看出,電壓環路中電壓補償器EA1的輸出電壓在當前的采樣周期是由它前一時刻的值和Vv-sam共同決定的,其關系式如式(4)所示。
??? Vp(k)=Vp(k-1)-K1Vv-sam(k)-(TK2-K1)Vv-sam(k-1)+TK2Vref(4)
同樣,電流環中的補償器EA2的轉移函數也可由圖1(a)得到
??? G2(s)=(5)
式中:K3=RczCcz;
????? K4=RciCcz。
??? 因此,轉移函數的離散表達式為
??? Vpwm(k)=Vpwm(k-1)+Vc(k)+
Vc(k-1)(6)
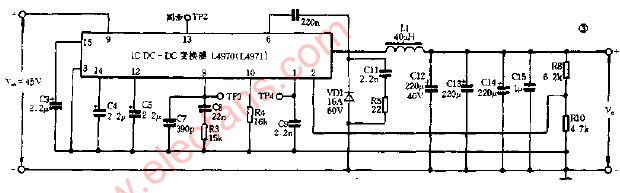
??? 圖1(b)是PFC變換器的DSP控制階段。該階段對3個主要電量:感應電流IL,整流輸入電壓|Vin|和輸出電壓Vout進行采樣。這些值經過采樣后再被轉換成數字量,參與DSP隨后的計算過程。與開關頻率比較而言,這3個信號中的兩個電壓信號就成了主要的低頻信號了。這里要求感應電流最好能被瞬時地反饋,這一點在模擬控制器中是很容易實現的,而在數字信號處理中由于采樣速率的限制和A/D轉換使得很難滿足這一要求。在實際的采樣算法中,采樣信號用來計算以后周期的脈沖寬度。
2??? 單周期單采樣方法的缺陷
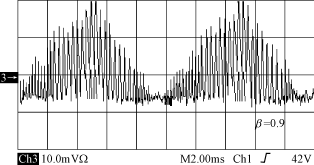
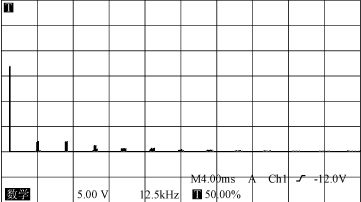
??? 對于一個數控的PFC來說,單周期單采樣(SSOP)使控制器相對模擬PFC而言對噪聲更加敏感。由于開關噪聲與電流傳感器有關并受其影響,在開關點上經常會出現高頻振蕩,而且振蕩將持續在一個相當長的周期內(如圖2所示),這些噪聲將影響系統的正常工作。最好的解決方法就是通過調整采樣點避開此采樣區間,即不固定點采樣算法。另一方面,可采用DSP芯片來限制采樣速率和A/D轉換。
??? 基于上述分析,SSOP采樣方法看似完美,但采用這種采樣算法后又會帶來新的問題,即如何在每一次開關循環中都確定一個固定的采樣點,上面所提到的條件又如何在任何時間都能得到滿足。在采用了SSOP方法的PFC應用中,輸入電流必須跟隨正弦輸入電壓,且輸出電壓必須始終為常數。占空比D從接近于1減小到最小值Dmin,而正弦交流電壓相應地從零變化到峰值。如果Dmin太小的話,就不能滿足SSOP算法的要求。最小占空比由式(7)給出。
??? Dmin=(7)
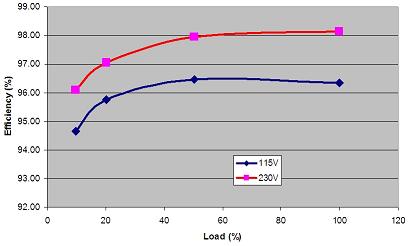
??? 通常,對于一個通用輸入電壓的PFC變換器來說,一般將其輸出電壓設計在385V左右。輸入電壓若為110V,Dmin可以滿足要求,但若為220V,Dmin就只能達到0.12~0.22,假定主電壓的變化范圍為10%,則Dmin將變得更低。由于D在每一個周期內從Dmin變化到1,因此,如果采樣過程能夠在開關導通時間內結束的話,就可能避開開關噪聲的干擾。所以,功率轉換開關S的導通時間便成了提高DSP控制PFC變換器開關頻率的主要限制因素。
3??? 采樣算法原理
??? 由于DSP本身具有很強的運算能力,所以,它能夠通過一種新穎的采樣算法來消除SSOP算法的缺陷。假定電路工作在固定頻率fs(=1/T)下,開關噪聲振蕩保持周期為τosc,采樣周期為τsam。為保證開關的抗噪聲性能,必須滿足以下要求:
??? 1)在開關轉換后的τosc間隔時間內不能進行采樣;
??? 2)在采樣的τsam間隔時間內不能進行開關轉換,因為任何擾動都有可能引起采樣結果發生錯誤。
??? 針對以上兩個條件,對采樣時刻D1T和D2T定義如下:
??? D1T=τosc(8)
??? D2T=2τosc+τsam(9)
??? 由式(8)及式(9)可知,一旦確定τosc和τsam后,D1T和D2T的值也就確定了。此時,就可以在控制器中應用Z域的穩定性分析。
??? 經計算可得最大開關頻率為
??? fs=(10)
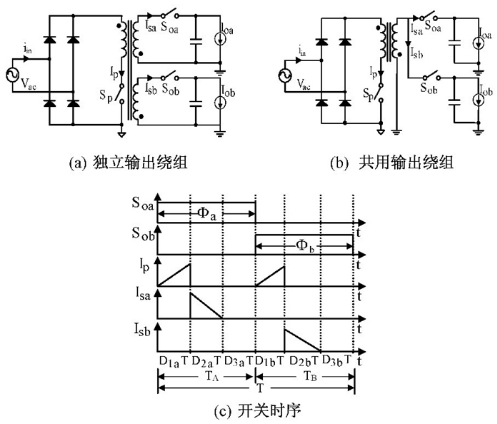
??? 本周期時間脈沖寬度DT是利用上一周期所獲得采樣值經計算得到的,再根據DT是否大于τosc+τsam來確定采樣時間是否合適。如果DT>τosc+τsam,如圖3(a)所示,D1T便是合適的采樣點;如果DT<τosc+τsam,則iL(D2T)被采樣,但不能直接用iL(D2T)來計算脈寬,因為,在iL(D1T)和iL(D2T)之間存在著一定的誤差(此誤差可通過電流補償環路中的積分算法來消除)。因此,必須先從iL(D2T)中求出iL(D1T)的值。
??? 1)DT<D1T=τosc
??? 在此條件下,兩個采樣點D1T和D2T都位于開關周期的截止時間段,如圖3(b)所示。這兩個點的采樣誤差為
??????? ΔiL1=iL(D1T)-iL(D2T)=(D2-D1)T(11)
??? 2)D1T
??? 在此條件下,采樣點D1T
???? iL(DT)-iL(D1T)=(D-D1)T(12)
??? iL(DT)-iL(DsT)=(D2-D)T(13)
??? 由式(12)及式(13)又可以得到
??????? ΔiL2=iL(D1T)-iL(D2T)=(D2-D)T-
(D2-D1)T(14)
4??? 實驗結果
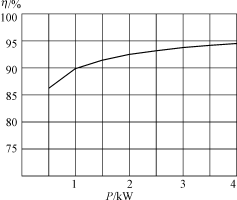
??? 將此算法運用到一臺2kW的PFC變換器中,為了提高效率并減少噪聲,選擇開關頻率為33kHz,采用DSPTMS320F240作為控制芯片,其最大采樣保持時間τsam約為1μs。開關轉換后的每一個振蕩周期τosc約為6μs。再根據式(8)及式(9),采樣點D1T
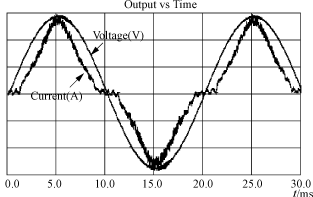
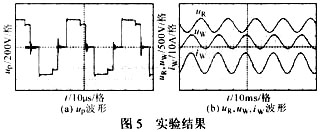
??? 圖5所示為在3種不同采樣模式下的感應電流波形。圖6為輸入電壓和輸入電流波形圖。經測量,輸入電流的總諧波失真為6.4%,功率因數為0.98。
5??? 結語
??? 本文提出了一種DSP控制的PFC的新穎的采樣算法,它節省了大量的系統資源,這些節省的系統資源又可以用來控制DC/DC或DC/AC變換器。該方案使整個系統僅用一片DSP芯片來控制,從而大大降低了硬件的成本。本文的方法和結論對于分析、設計和調試所有含開關的數字采樣電路均有實用參考價值。
 電子發燒友App
電子發燒友App













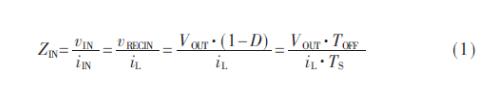










評論