一、緩沖正向轉換器

　　您是否一直為如何挑選緩沖器組件而煩惱？計算出要添加多少電容和電阻是一項頗具挑戰性的工作。下面就來介紹一條解決這一難題的捷徑。

　　圖 1 顯示了正向轉換器的功率級。該轉換器由變壓器運行，該變壓器將輸入電壓耦合至次級電路，再由次級電路完成對輸入電壓的整流和濾波。反射主電壓和變壓器漏電感形成低阻抗電路，當 D2 通過一個這樣電阻而被迫整流關閉 （commutate off） 時，通常需要一個緩沖器。D2 可以是一個硅 p-n 二極管，該二極管具有一個必須在其關閉前實現耗盡的逆向恢復充電功能。這就積累 （loads up） 了漏電感中的過剩電流，從而導致高頻率振鈴和過高的二極管電壓。肖特基二極管和同步整流器也存在類似情況，前者是因為其大結電容，后者是因為其關閉延遲時間問題。

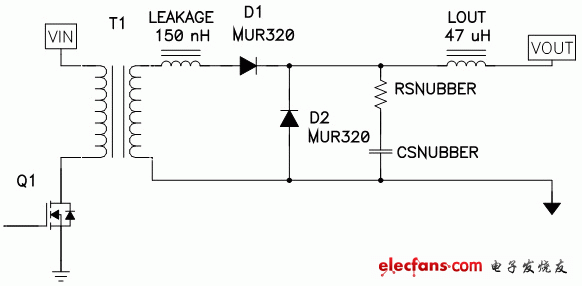
　　圖 1 漏電感延緩了 D2 關閉

　　圖 2 顯示了一些電路波形，頂部線跡為 Q1 漏電壓，中部線跡為 D1 和 D2 結點處的電壓，底部線跡為流經 D1 的電流。在頂部線跡中，您可以看到當 Q1 打開時，其漏電壓被降至輸入電壓以下，這樣就使得二極管 D1 電流增加。如果 D2 沒有逆向恢復充電功能，當 D1 電流等于輸出電流時，結點電壓就會上升。由于 D2 具有逆向恢復充電功能，因此 D1 電流會進一步增加，這便開始消耗電荷。一旦電荷耗盡，二極管便關閉，從而導致增加的結點電壓進一步提高。請注意，電流會不斷增加直到結點電壓等于反射輸入電壓為止，因為在漏電感兩端有一個正電壓。隨著電流的增加，該電流將對寄生電容進行充電并導致電路中振鈴和損耗更大。

　　圖 2 當 D2 關閉時 D2 會引起過多的振鈴

　　這些振鈴波形也許是人們所無法接受的，因為它們會引起 EMI 問題或帶來二極管上讓人無法接受的電壓應力。跨接 D2 的 RC 緩沖器可以在幾乎不影響效率的同時大大減少振鈴。您可以利用下面的方程式計算得出振鈴頻率（請參見方程式 1）：

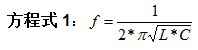
　　但是您如何知道電路中 L 和 C 的值呢？竅門就是通過在 D2 兩端添加一個已知電容值的電容以降低振鈴頻率，這樣您就得到了兩個方程式以及兩個未知項。如果您添加了正好可以減半振鈴頻率的電容，那么就會使求出上述值變得更加輕松。要想降低一半頻率，您需要一個 4 倍于您一開始使用的寄生電容的總電容。然后，只要將所添加的電容除以 3 就可以得到寄生電容。圖 3 顯示了頻率為最初振鈴頻率一半時 D2 兩端 470 pF 電容的波形。因此，電路具有大約 150 pF 的寄生電容。請注意，只添加電容對振鈴的振幅作用很小，電路還需要一些電阻來阻尼振鈴。這就是電容因數 3 是開始的好地方的另一個原因。如果選擇的電阻適當，那么該電阻就可以在對效率最小影響的同時提供卓越的阻尼效果。阻尼電阻的最佳值幾乎就是寄生元件的典型電阻（請參見方程式 2）。

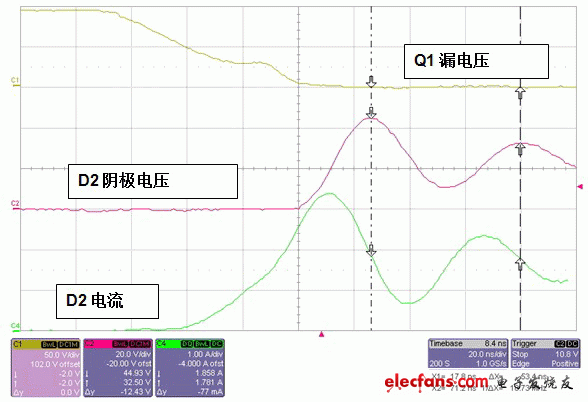
　　圖 3 將振鈴頻率提高兩倍完成寄生計算

　　使用具有 35 MHz 振鈴頻率的方程式 1 以及一個 150 pF 的寄生電容可以計算得出漏電感為 150 nH。把 150 nH 代入方程式 2 得出 一個大約為 30 Ohms 的緩沖器電阻值。圖 4 顯示了添加緩沖器電阻的影響。振鈴被完全消除且電壓應力也從 60V 降到了 40V。這樣我們就能選擇一個更低額定電壓的二極管，從而實現效率的提高。該過程的最后一步是計算緩沖器電阻損耗。使用方程式 3 可以完成該過程的最后一步，其中 f 為工作頻率

　　一旦完成計算，您就需要確定電路是否可以承受緩沖器中的損耗。如果不能的話，您就需要在振鈴和緩沖器損耗間進行權衡。如欲了解如何選擇最佳阻尼電阻的詳情，請參見第 3 頁的圖 3《電源設計小貼士 4》。

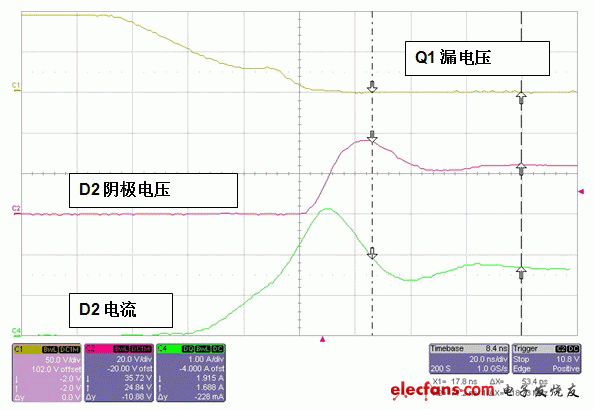
　　圖 4 選擇適當的緩沖器電阻器能完全消除振鈴

　　總而言之，緩沖正向轉換器是一個簡單的過程：1） 添加電容以減半振鈴頻率；2） 計算寄生電容和電感；3） 計算阻尼電阻以及電感 4） 確定電路損耗是否在可以接受的范圍內。

　　二、緩沖反向轉換器

　　之前，我們介紹了如何對正向轉換器輸出整流器開啟期間兩端的電壓進行緩沖。現在，我們來研究如何對反向轉換器的 FET 關斷電壓進行緩沖。

　　圖 1 顯示了反向轉換器功率級和一次側 MOSFET 電壓波形。該轉換器將能量存儲于一個變壓器主繞組電感中并在 MOSFET 關閉時將其釋放到次級繞組。由于變壓器的漏極電感會使漏電壓升至反射輸出電壓 （Vreset） 以上，因此 MOSFET 關閉時通常會需要一個緩沖器。存儲于漏極電感中的能量可使 MOSFET 產生雪崩現象，因此要添加一個由 D1、R24 和 C6 組成的鉗壓電路。該電路的鉗位電壓取決于漏電的能量大小以及電阻器的功率消耗。更小值的電阻雖然可以降低鉗位電壓，但會增加功率損耗。

　　圖 1 FET 關斷時漏極電感形成過電壓

　　圖 2 顯示的是變壓器主繞組和次級繞組的電流波形。左側是 MOSFET 開啟時的簡化功率級。輸入電流通過漏極電感和互電感的串聯組合斜坡上升。右邊顯示的是關斷期間的一個簡化電路。此處，電壓已反向至輸出二極管和鉗位二極管正向偏置的點。我們展示了反射到變壓器一次側的輸出電容器和二極管。兩個電感為串聯，并在 Q1 關斷時初始傳輸相同的電流。這就是說關斷以后輸出二極管 D2 中并未立即出現電流，同時總變壓器電流在 D1 中流動。漏極電感的電壓是鉗位電壓和重位電壓之間的差，且往往會快速釋放漏電。如圖所示，經過簡單計算便可得到分流至緩沖器的能量大小。因此您可以通過縮短釋放漏極電感中能量的時間，來減少分流能量。提高鉗位電壓可以實現這一目標。

　　圖 2 漏極電感竊取輸出能量

　　有趣的是，您可以在鉗位電壓和緩沖器功耗之間計算得到一個折中值。如圖 2 所示，進入鉗位電路的功率等于平均鉗位二極管電流乘以鉗位電壓（假設一個恒定鉗位電壓）。重排某些項后，我們可以得到 ? * F *L * I2，其與間斷反向轉換器輸出功率相關。這種情況下，電感為漏極電感。該表達式稍稍令人有些吃驚，因為其中的功率損耗不僅僅是存儲于漏極中的能量。它始終都較大，但卻依賴于鉗位電壓。圖 3 顯示了這種關系。該圖繪出了漏極電感能量損耗標準化損耗與鉗位電壓和重位電壓之比的對比關系。在鉗位電壓高值位置，緩沖器損耗接近漏極電感中的能量。由于減小電阻降低了鉗位電壓，因此能量從主輸出分流，同時緩沖器損耗急劇增加。在 1.5 Vclamp/Vreset 比時，其幾乎三倍于漏極電感存儲能量相關的損耗。

　　　　圖 3 增加鉗位電壓可降低緩沖器損耗

　　碰巧的是，漏極電感通常為磁化電感的 1% 左右。這讓圖 3 看起來更為有趣，其向我們表明降低鉗位電壓會對效率產生的影響，所以只需縱軸變為效率損耗。因此，將鉗位比從 2 降到 1.5 會對效率產生 1% 的影響。

　　總之，反向轉換器的漏極電感可對電源開關產生不可接受的電壓應力。RCD 緩沖器可以控制這種應力。但是，可以在鉗位電壓和電路損耗之間有一種折中方法。

　　三、穩壓器的輸出電壓精度分析

　　雖然輸出電壓不斷下降而穩壓要求正變得越來越高，但是您的任務可能并非像其表面上看起來那么困難。即使必須要使用 1% 或更大的容差電阻來進行設計，但您仍然可以得到非常精確的輸出電壓。

　　圖 1 顯示了一款典型的電源調節電路。輸出被分流降壓，并與參考電壓進行比較。差異被放大，并用于驅動調節環路。乍一看，您可能會認為這一方案僅限于兩倍電阻容差精度。幸運的是，實際并非如此；精度還是輸出電壓與參考電壓之比的強函數。

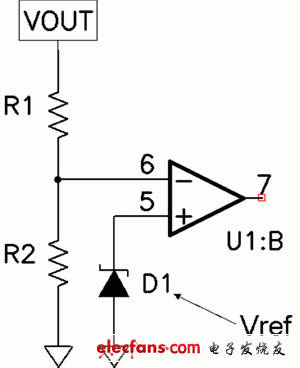
　　　　圖 1 輸出精度是分壓器比、基準精度和誤差放大器補償的函數

　　三種不同的情況可以非常容易地說明這一比率。第一種情況是假設一點分壓也沒有，換句話就是說輸出電壓等于參考電壓。很明顯，這種情況下沒有電阻分壓誤差。第二種情況是假設輸出電壓大大高于參考電壓。在這種情況下，R1 大于 R2。分壓器誤差是電阻容差的兩倍，從而得到一個方向變化的 R1 值，以及往另一個方向變化的 R2 值。第三種易于說明的情況是假設輸出電壓是參考電壓的兩倍。在這種情況下，額定電阻值相等。因此，如果電阻容差以反方向變化，則分壓器方程式頂部隨著該容差值變化，而分母變為零。

　　圖 2 顯示了輸出精度，其為參考電壓與輸出電壓對比關系的函數。（詳細推導過程請參見附錄。）簡化之后，分壓器精度為 （1 – Vref/Vout）*2*容差，其與我們通過檢查得到的三個數據點相關。我們對該方程式進行了一些簡化處理，但對大多數電阻容差來說都應該足夠精確。

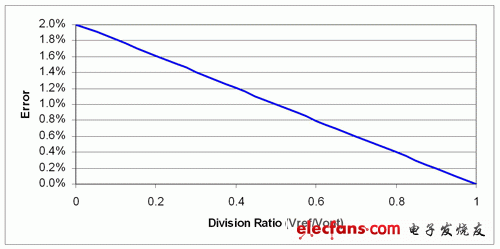
　　圖 2 輸出精度很直觀：（1-Vref/Vout）*2*容差（顯示的 1% 電阻）

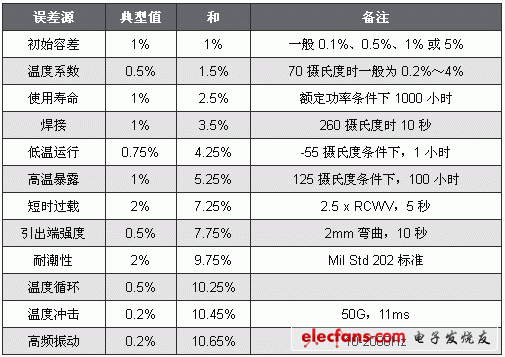
　　有趣的是，這樣給低壓輸出帶來了更高的精度。許多 IC 參考電壓范圍為 0.6～1.25 V 之間，輸出電壓降至這一范圍時會帶來 1% 或更高的精度。表 1 給出了您可能需要了解的一些信息，這些信息是典型電阻器產品說明書的電阻誤差術語匯編。在設計中，該列表會較難理解。大多數工程師都止步于初始容差，然而列表中還有一些或許不應被忽略的誤差項。表格中的每一項都有其微妙的影響。例如，沒有指定具體的溫度系數范圍，而實際上兩個電阻都可能隨溫度變化以相同方向變化，并且不會在相反的極端。在對一些經驗豐富的設計工程師進行簡單調查后，得出的結論是假設 1% 容差電阻的 2.5% 精度可在極端情況和合理成本之間得到一個合理的折中方案。

　　表 1 電阻容差可相加

　　總之，提供較好的低壓輸出精度并非是一項令人畏懼的任務，因為低分壓器比本身就較為精確。

　　下個月我們將討論獲得負電壓的一種有趣的電源拓撲，敬請期待。

　　本文最后面列出了一些我撰寫的其他《電源設計小貼士》文章。如欲了解本文章內容及其他電源解決方案的更多詳情，敬請訪問：www.ti.com.cn/power。

　　附件 - 求解計算頂部分壓器電阻值，其為分壓器比 （R） 的函數：

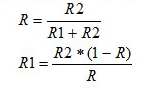
　　重寫表達式為電阻容差 （T） 的函數：

　　代入 R1：

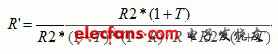
　　頂部和底部乘以 R/R2：

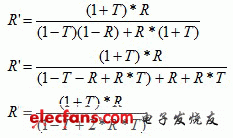
　　除以 R，然后減去 1，得到誤差：

　　四、輕松創建多個負輸出電壓

　　因特網協議語音傳輸 （VoIP） 電話的出現帶來了對于生成多個高壓負輸出的需求，這些電壓軌用于驅動電話線路。當線路處在通話模式時，一般會有一個 –24V 輸出來提供環路電流，同時通常會有另外一個或兩個負輸出來驅動電話振鈴。有趣的是，就每條電話線路而言，這些負載相互排斥，也就是說您不能使電話同時響鈴和通話。然而，一個系統中可能會有多條電話線路，從而產生許多負載情況。這些系統通常由一個 12V 的電源供電，其已經與輸入功率隔離，因此一般不再需要二級隔離。功率電平一般低于 25W，調節要求通常在 3% 到 10% 范圍內。

　　反向拓撲結構看起來是這種應用的不二選擇。功率電平與反向拓撲結構一致。利用反向拓撲結構可輕松地生成多個高壓輸出，而反向拓撲結構已為人們所了解。但是，反向拓撲結構也存在諸多不足之處：該拓撲包括會過度振鈴的非鉗位電源開關電壓，；其通常需要一個二級輸出濾波器；零到滿負載的交叉調節不能為 3%。

　　圖 1 顯示了一種替代方法。您認識這種拓撲結構嗎？讓我們來研究這種拓撲結構具有的一些優點，假設所有負載僅為 -27V 輸出。

　　關閉開關，使 C16 鉗位控制電源開關 （Q1）。電源開關開啟時，輸出整流器 （D2） 由 C16 鉗位控制。因此，通常不會出現與反向拓撲結構相關的振鈴。另外，流經耦合電感的輸入及輸出電流可以為持續，這極大地簡化了輸入和輸出濾波器。這種拓撲結構是一款 C’uk 轉換器。普通工程師對這種拓撲結構不是很了解，這成為實施該拓撲結構的難點。這主要是因為只是偶爾使用 C’uk，抑或是工程師在大多數時候甚至都沒有考慮它。

　　圖 1 這種獨特的拓撲結構可提供非常好的交叉調節，奧妙何在？

　　VoIP 電話的電源對成本、功耗都極為敏感，并且需要一定的 （5%） 交叉調節。它們都是一些大容量系統，具有較大的價格壓力。它們一般將電池作為備用電源，其每一瓦特都十分珍貴。需要對所有輸出進行較好地控制，以實現交叉負載并保護下游放大器。由于振鈴的存在，這一整套要求成為反向拓撲結構一個難題，并需要預負載或者額外的功率調節電路。表 1 顯示了 C’uk 轉換器在這種應用中具有優勢。

　　該表列出了極端條件負載極限的一些交叉調節結果。在本例中，利用流經 R17、R18 和 R20 的加權電流，輸出電壓同樣也得到了調節。這樣便聚集了誤差，同時提供比 5% 更佳的極限交叉調節，其沒有預負載或額外調節電路。通過增加該輸出的加權，我們可以進一步改善一個輸出的調節，從而負影響另一個輸出的調節。

　　即使假設 C’uk 轉換器沒有預負載，其效率也比反向拓撲結構好 2%。這是通過使用更低電壓的開關和二極管實現的，因為電路中缺少振鈴。

　　表 1 所有負載組合的輸出精確度都優于 5%

　　總之，盡管一般不考慮使用 C’uk 轉換器，但 C’uk 轉換器的確非常適用于這種應用。這種應用要求：1）無隔離；2）正-負電壓轉換；3）多輸出；4）良好的交叉調節；5）高效率；以及6）低成本/最少組件數量。

　　五、注意那些意外諧振響應

　　您曾經將輸入電壓接通到您的電源卻發現它已經失效了嗎？短暫的輸入電壓上升時間和可產生兩倍于輸入電源電壓的高 Q 諧振電路可能會是問題所在。如果您迅速中斷感應元件中的電流便會出現類似問題。會出現這類問題的一些情況包括熱插拔電路或者試圖開放輸入向電磁干擾 （EMI） 濾波器時。

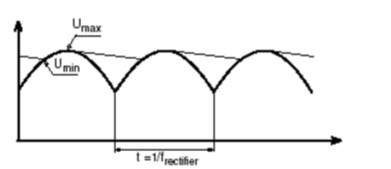
　　圖 1 顯示了帶開關輸入的簡化濾波器示意圖。電路的電感可以為有意的也可以是偶然發生的，例如：以太網供電 （PoE） 系統的長通電線路。該圖還顯示了步進的輸入電壓波形，以及阻尼系數小于 1 時的生成輸出電壓。（大于 1 的阻尼系數沒有過沖。）更低阻尼系數的響應形式如下：

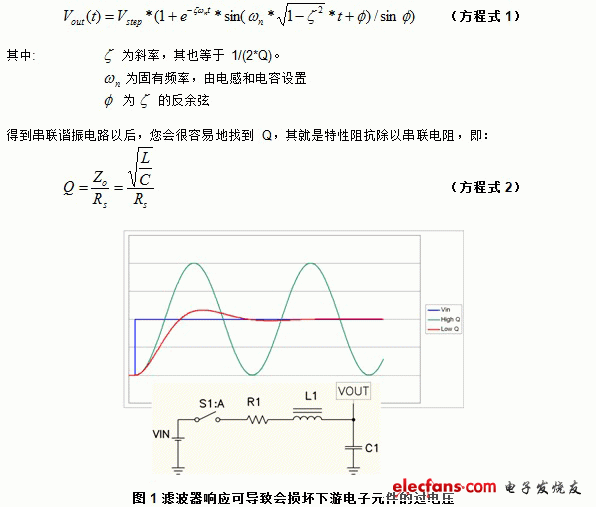
　　圖 1 濾波器響應可導致會損壞下游電子元件的過電壓

　　高 Q（低阻尼）系統為無阻尼，而濾波器輸出電壓可振鈴至兩倍輸入源 （Vin）。低 Q 系統會限制峰值振鈴電壓。

　　圖 2 顯示了過沖百分比，其為阻尼比率的函數。使用 0.4（1.25 Q）阻尼比率可將振鈴電壓限定到源電壓的 130%。由于阻尼電阻的額外損耗或將一個電阻與電容串聯產生的濾波損耗可能是不可接受的，因此這樣做或許并不切實際。如果您的設計不能容忍這些損耗，那么您需要添加一些額外的組件。例如，利用串聯電阻以及同濾波器電容 （C1） 并聯的電容器可以進一步阻尼電路。您也可以使用熱插拔電路來限制濾波器的峰值電流；或者您可以將一個二極管同電感器并聯，以提供低阻抗電容充電。

　　事情并非如看起來那樣糟糕。電感器的電流會令其飽和，同時電容充電可以通過比預計更低的串聯電感進行。如果電感飽和，則濾波器特性阻抗會像 Q 一樣下降，從而減少過沖。要檢驗在高 Q 系統中其是否會出現這種情況，請利用電壓階躍除以系統特性阻抗來計算峰值電流。之后，請參閱電感產品說明書確定其是否會飽和。

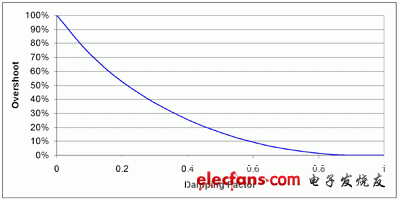
　　圖 2 增加阻尼比率（降低 Q）來減少過沖

　　總之，階躍輸入電壓帶來的濾波器振鈴可導致對下游電子元件有破壞性影響的電壓。特別是如 PoE 的系統，在使用低損耗陶瓷電容和一些不飽和的電感時它們往往為高 Q，則上述電壓便成為問題。如果電壓達到不可接受的水平，則這些系統會需要更多的阻尼、電流限制或者一種替代充電方法。下面將介紹一種確定您是否存在問題的簡單過程：

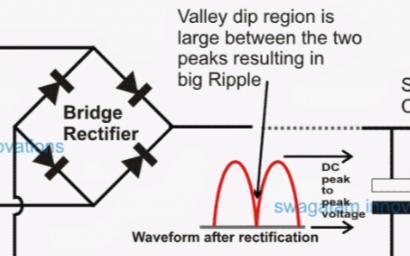
　　六、請注意電容 RMS 紋波額定電流！

　　電源中常常被忽略的一種應力是輸入電容 RMS 電流。若不正確理解它，過電流會使電容過熱和過早失效。在降壓轉換器中，使用下列近似式，根據輸出電流 （Io） 和占空比 （D） 可以很輕松地計算出 RMS 電流：

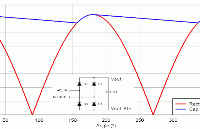
　　圖 1 給出了該表達式的曲線圖；它是一個圓形，其中，50%占空比時達到最大值0.5，并在 0% 和 100% 占空比時有 2 個零交叉。該曲線在 50% 占空比附近對稱。在 20% 和 80% 之間，RMS 電流和輸出電流之間的比大于 80%。使用這一范圍的占空比，您可以將 RMS 電流粗略估計為 1/2 最大輸出電流。在這一范圍之外，您需要進行相應的計算。

　　圖 1 在 1/2 輸出電流處出現降壓輸入電容RMS電流峰值

　　在過去幾年中，陶瓷電容器的容積效率和成本兩方面都取得了巨大的進步。陶瓷電容器現在成為繞過電源功率級的首選。但是，它們的低 ESR 在電源中會產生許多困擾，例如：EMI 濾波器振蕩和意外電壓浪涌（參見《電源設計小貼士 20》）。并聯電解電容常常用于抑制這些高 Q 電路。這些情況下，您應該注意電解質中的紋波電流，因為大量的電源紋波電流會最終進入電解電容。圖 2 顯示了一個帶輸入電容的 100 kHz 轉換開關例子，其輸入電容由一個同電解電容器并聯的 10 uF 陶瓷電容組成，而該電解電容器包含 0.15 歐姆的等效串聯電阻 （ESR）。假設電解電容器的電容比陶瓷電容器的大，在這種情況下，約 70% 的 RMS 電流出現在了電解質中。要減少該 RMS 電流，您可以增加陶瓷電容、工作頻率或者 等效串聯電阻（ESR）。通過電容電流的傅里葉級數可以繪制出這一曲線，從而計算每個諧波（多達 10）的電解電容器電流，并重新組合諧波來計算電解電容器的總 RMS 電流。請注意，陶瓷電容的電流與 ESR 的電流在相位上相差 1/4 周期，因此必須將它們看作是矢量。如果您不想在這些計算方面花費時間，那么您可以通過一個電流源和三個無源組件輕松地對該電路進行仿真。

　　圖 2 使用不同電容類型時請注意電解電容電流

　　總之，要注意輸入電容中的 RMS 電流，因為過電流應力會降低電容的可靠性。組合電容類型時更需特別注意，因為陶瓷電容通常會允許足夠高的紋波電壓在并聯電解電容中形成過電流狀態。這一問題的解決方法是增加如下一項或多項：工作頻率、陶瓷電容數量、電解電容 ESR 或其 RMS 額定電流。

　　注：

　　下面是輸入電容中RMS電流的推導過程，其假設電感無窮大。它以矩形脈沖（D0.5*Ipk）的RMS電流作為開始，并去除了DC組件（D*Ipk）。

　　
?

??????下次繼續討論電源電路中和避免一些常見的誤差放大器使用錯誤等問題，敬請關注。



?