采用SPCE061A單片機對輸入的20Hz~100KHz的音頻信號通過A/ D采樣,獲得各點電壓值。用快速傅立葉(FFT)技術對A/D采得的數字量進行8次蝶形運算,獲得各點幅值。使得頻率分辨力小于100Hz,可測得頻差小于100Hz的頻率分量的功率值。分別由電壓值和各點幅值求出輸入信號的總功率和各頻率分量的功率和,發現各頻率分量的功率和與輸入信號的總功率間的誤差小于5%。根據各頻率分量的幅值,我們可以找出輸入信號的分率成分。同時由LCD顯示信號總功率及前兩個頻率分量的頻率值和功率值。分析頻率時用到的FFT技術,同時又可移植到波形失真度測量領域,對失真度進行精確計算。
關鍵詞:SPCE061A、A/D采樣、FFT處理、頻率分析、功率計算、周期判斷
一、系統方案論證與比較
1、系統要求
設計、制作一個可分析音頻信號(200Hz~10KHz,100mV~5V)頻率成分,并可測量正弦信號失真度的輸入阻抗為50Ω的儀器。基本要求頻率分辨力100Hz,檢測輸入信號的總功率和各頻率分量功率和,分析時間5S。發揮部分要求增加頻率分辨力,并能判斷輸入信號周期,以及分析正弦波失真度。
2、方案比較
2.1輸入預處理部分
對輸入音頻信號進行采樣,要求輸入信號的電壓范圍不能有負值,并保證被轉換電壓的幅值范圍在A/D處理范圍內。現輸入音頻信號的電壓峰-峰值范圍為(0~5V),要保證輸入信號的幅值為正,必須進行預處理,抬高電壓。
方案1:外加直流電源,串、并聯電阻抬高電壓。要精確抬高輸入信號的電壓,則必須精密計算串、并聯電阻的阻值。而且選擇的電阻要精密,對材料要求高。外接電阻,將消耗輸入信號的功率,對題目要求的測量輸入音頻信號的功率有影響。
方案2:利用集成運放,外接直流電壓,進行加法、除法處理信號電壓。用運放將輸入信號與直流信號進行加法操作,不改變輸入信號的頻率,不影響后面對頻率分量的分析。做除法運算,只是改變了信號各點的電壓值,保證了A/D工作范圍。
方案 3:在電壓抬高的基礎上,進行反混疊濾波處理。采樣頻率大于20KHz信號頻率時,會產生混疊。為避免混疊,要么提高采樣頻率,要么采用濾波電路。前者加大了對A/D的要求,增大了單片機控制的難度。后者可對大于10KHz的信號產生抑制作用,減少干擾。
綜合考慮,我們選擇采用集成運放抬高電壓,反混疊濾波器對輸入信號進行預處理。
2.2、信號采樣
方案1:由單片機自帶A/D進行采樣。如SPCE061A,芯片內部集成了10位的A/D轉換,其最大采樣頻率可達到96KHz。完全可對10KHz的音頻信號采樣,并保證分辨力小于100Hz的要求。同時可以不用考慮A/D與單片機兼容的問題。
方案2:外接A/D轉換。如8位的A/DTLC5510,雖然轉換速度可以達到2M/S,但是其精度不高。基本部分要求計算輸入信號功率和各頻率分量功率和,并計算二者誤差,而8位A/D采得的精度不夠,必增大誤差。外接A/D,將增大引入干擾的可能。不利于系統的穩定。
方案3:對于基礎部分和發揮部分別用A/D轉換,基礎本分用高位的A/D保證精度,發揮部分用高速A/D保證采樣速率。
結合實際,SPCE061A已能滿足要求,既能達到精度要求,又能達到采樣速率的要求,所以采用方案1。
3、綜合描述
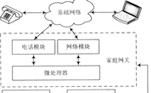
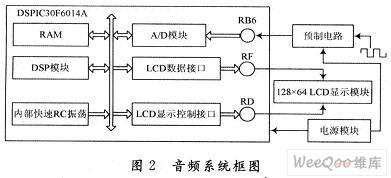
系統框架如圖(1)所示。圖中輸入信號的電壓范圍(峰-峰值)為100mV~5V,包含的頻率成分范圍為200Hz~10KHz。外部處理即對輸入信號進行低通濾波,保證測量的信號頻率是小
輸入
信號
?
外部
處理
?
SPCE061A
A/D采樣與FFT處理
?
LCD顯示
?
鍵盤
?
(1)系統框架結構
?
于10KHz的信號。由于SPCE061A電壓的直接測量范圍為0~3.3V,所以對于寬范圍的電壓信號,必須進行壓值處理,使其在測量范圍內。SPCE061A單片機本身有A/D轉換功能,所以在芯片內部就可完成采樣。再由單片機完成FFT數據處理。LCD用于顯示頻率與功率。鍵盤用于切換功率與頻率回放顯示、實現暫停等功能。
二、理論分析與計算
1、放大器設計
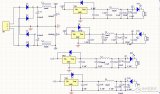
由于輸入音頻信號的電壓范圍(峰-峰值)為100mV~5V。音頻信號無法預計其幅值,當信號的峰-峰值為100mV時,幅值小,受外界信號干擾大,容易引起測量不準。所以要采用放大電路。系統采用2個OP07先抬高輸入信號,再對信號衰減。
圖(2)放大器設計
?
如圖(2)所示:電壓V1為信號的輸入電壓,V2為外接直流電壓(V2=5V),V3是提升后的電壓。首先將輸入信號V1與直流分量V2進行求和,得V3與輸入信號V1相位相反。再經過一次反向除法運算,得到一個與輸入信號相位相同的衰減信號VO? 。
因為? ,即 ;則有?? ;
當 為小信號,即 的峰值為100mV:對應的最小 V;相對以前的10mV,增大了100倍,避免了干擾。
又因為??? ;則有???
由上述計算知道:已在SPCE061A的測量范圍(0~3.3V)。
2、功率譜測量方法
輸入音頻信號的頻率范圍為200Hz~10KHz,要求頻率的分辨力為100Hz。則需要對音頻信號采樣,由A/D轉換,經FFT處理,獲得各點的幅值,經過運算可以得到各頻率分量的功率。
首先確定采樣頻率fs,由于音頻信號的頻率范圍為200Hz~10KHz,根據采樣定理,必須保證fs≥20KHz,結合分辨力100Hz的要求,我們確定fs =25.6KHz。
頻率分辨力ΔF= fs/N。現確定fs =25.6KHz,要保證頻率分辨力為100Hz,則應取N= 25.6K/100=256點。則第n點的頻率fK=100nHz。對音頻信號采樣后的各點值,需用FFT原理處理,得各點的正弦信號的幅值Un。則各頻率分量的功率為 。
3、周期性判斷方法
?? 音頻信號可看成是N次諧波的疊加,則音頻信號里必有一個最大的頻率分量,我們可近似的將輸入音頻信號的周期看成是最大頻率分量的周期。最大的頻率分量可以在做頻譜分析時通過各分量的相互比較得出,設最大頻率分量的頻率為fmax。那么音頻信號的周期T=1/fmax 。
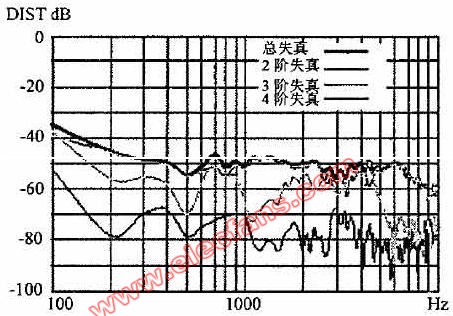
4、失真度測算
失真度計算公式:?? 為第n點諧波功率, 為基波功率。將測得的各頻率分量的功率代入上式計算,可得失真度K。
三、電路與程序設計
1、電路設計
1.1、反混疊濾波電路??
圖(3)反混疊濾波電路
?
在應用FFT變換時需要對連續的時間信號進行采樣,當采樣頻率fs>2*fh時,采樣后的頻譜中將有一部分重疊,導致采樣后的信號x(n)的頻譜與原始信號的頻譜不一致,因此需要加一反混疊濾波器。如圖(3)低通濾波器,圖示二階低通VCVS? 濾波器的截止頻率為10KHz,將抑制高于10KHz的音頻信號輸入。
1.2、SRAM擴展電路
進行頻譜分析時,要對音頻信號采集的數字量進行FFT處理。單片機計算時要用到兩個256個浮點型值的正、余弦表。總共占用RAM 4*256*2=2048=2K。而SPCE061A的RAM只有2K,故在計算時RAM資源并不充分,需要擴展。我們采用SPR4096進行擴展。SPR4096具有4K×8bit的RAM,512K×8bit的flash。擴展電路連接如圖(4)SPR4096與SPCE061A連接圖。
圖(4)SPR4096與SPCE061A連接圖
?
2、程序設計
LH=N/2
J=LH
N1=N-2
?
I=1,N1
?
I≥J
?
T=X(I)
A(I)=X(J)
A(J)=T
?
K=LH
?
J
J=J+K
?
J=J-K
K=K/2
?
Y
?
Y
?
N
?
N
?
圖(5)倒位序流圖
?
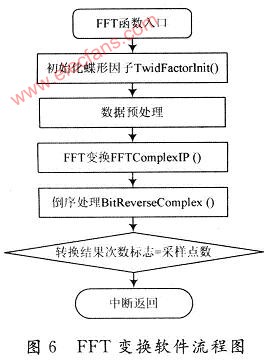
如右圖(5)所示為FFT蝶形運算處理的一個倒位序流程圖。FFT算法在實現時就是3個嵌套循環,而倒位序的實現可以通過查表和算法實現。自制倒位序查詢表,將占用較多的RAM資源,不利較多取樣點的計算。通過函數自己還原倒位序,將留出更多的RAM空間利于采集更多的點,增大分辨力,提高功率計算的準確性。
Y
?
?FFT算法:
N
?
?;
for L=1:M? ;
?;
for J=0:B ;
??? ;
for K=J: :N? ;
????? ;
????? ;??????????????????????????????
end
end
圖(5)倒位序流圖
?
end
四、指標測試
1、測試方案
測試儀器:
直流穩壓電源、交流毫伏表、四位半數字萬用表
(1)輸入阻抗測試
外接直流電壓U,測輸入電流I。則RIN=U/I。
(2)功率測量
外接標準的正弦信號,調節信號的頻率與幅值,根據? (U為信號的峰值),分別測量各信號的功率。
(3)其它指標
經壓值處理電路,知電壓UO(0~2.5V),在系統的處理電壓(0~3.3V)范圍內。設定的單片機采樣率為25.6KHz,大于10KHz,能完成題目要求分析的信號范圍。5S刷新一次,實時顯示信號總功率和前兩個頻率分量都可在LCD上觀察。
輸入信號的周期T可近似看作其最大頻率分量的周期TMAX ,最大頻率分量的頻率為fMAX。則:T=TMAX=1/fMAX 。
2、測試結果
(1)輸入阻抗測試數據
測得R=49.5Ω。
(2)功率測量結果
|
電壓峰-峰值 |
頻率 |
測量功率 |
實際功率 |
誤差 |
|
2V |
100Hz |
0.03994W |
0.04W |
0.15% |
|
2V |
500Hz |
0.03912W |
0.04W |
2.2% |
|
2V |
1KHz |
0.03887W |
0.04W |
2.8% |
|
2V |
10KHz |
0.03812W |
0.04W |
4.7% |
|
1V |
800Hz |
0.00965W |
0.01W |
3.5% |
|
3V |
800Hz |
0.08976W |
0.09W |
0.3% |
3、結果分析
? 由表(1)知系統在頻率較低,電壓值大時時測量的準確度高。題目要求的基礎部分都完全達到要求。
發揮部分,頻率分辨力的大小直接影響信號分析的靈敏度。頻率分辨力越小,信號的動態測量范圍越大,輸入信號周期T越精確。
 電子發燒友App
電子發燒友App




















評論