為解決高空背景條件下紅外低信噪比運動點目標的檢測問題,本文提出了一種基于膨脹累加的檢測方法.運用形態膨脹運算能夠使同一目標處于不同幀上的能量仍然能夠實現有效的累加,從而達到目標增強的目的.同時本文還采用小波變換預處理的方法,對圖像中相關的1/f噪聲進行白化.本文對這一方法進行了大量的仿真實驗和詳細的理論分析.實驗證明該算法能夠快速穩定地檢測出信噪比為2的運動點目標.
關鍵詞:紅外圖像處理;紅外目標檢測;小波變換
Moving Infrared Low SNR Target Detection algorithm
XIONG Hui,SHEN Zhen-kang,WEI Ji-bo,LI Ji-cheng
(Institute of Electronic Science and Engineering,National University of Defense Technology,Changsha 410073,China)
Abstract:This paper is presented to resolve the moving infrared target detection problem under the condition of low SNR.The scheme of multi-frame accumulation is often adopted in low SNR infrared target detection,but for moving low SNR target,this simple accumulation scheme maybe degrades greatly.In this paper,a detection algorithm based on morphological dilation before accumulation and tracking before detection is proposed.The dilation operation enables the energy of the same target in different frames can be accumulated effectively in spite of the movement of target,thus we can reach the aim of enhancing the target.A preprocessing algorithm using wavelet transform is also adopted to remove the correlation of 1/f noise in parallel scanned infrared image.The whole algorithm is well analyzed and simulated with infrared image sequence.A high performance is reached and the experimental result indicates that the algorithm can effectively detect the moving target with SNR=2.
Key words:infrared image processing;infrared target detection;wavelet transform;mathematical morphology
一、引 言
在紅外尋的制導過程中,需要能夠盡快地截獲并鎖定跟蹤目標,由于紅外傳感器與目標之間的距離很遠(通常為幾十公里甚至上百公里),目標在像平面上的成像僅為點目標,并且淹沒在各種雜波背景中.通常的點目標的檢測方法采用多幀累加來提高信噪比,這種簡單的累加方法在目標幀間移動很小時可以有效地抑制噪聲并起到增強目標的作用.但對于運動速度較大的目標(平均幾幀圖像移動一個象像素),這種簡單的累加方法并不能夠實現有效的能量積累,很難檢測出低信噪比并處于快速運動中的點目標.
為解決高空背景中低信噪比運動點目標的檢測問題,本文提出了一種基于膨脹累加、檢測前跟蹤的算法.將經過白化預處理的圖像作形態膨脹運算之后再進行累加,這樣仍然可以使同一點目標在不同幀上的能量累加到同一像素點上,起到突出目標的作用.邊檢測邊跟蹤利用目標候選點在連續幀上的信息剔除虛警假目標,采用航跡關聯判決的方法來提高算法的抗干擾性能.
本文采用紅外線列掃描圖像序列對算法進行模擬. 紅外線列掃描圖像主要有兩種噪聲:圖像平面上的白噪聲和線列掃描方向上的非平穩1/f噪聲.本文采用小波變換的方法對線列掃描方向上的1/f噪聲進行白化預處理.實驗證明,該算法獲得了很好的預處理效果.膨脹累加算法能夠快速檢測出信噪比為2的點目標.
二、低信噪比運動點目標的檢測算法
1.圖像預處理
高空背景可近似看作均勻輻射背景,傳感器的內部噪聲將起主要作用.在線列紅外圖像中主要存在不相關的白噪聲和線列掃描方向上相關的1/f噪聲.可以合理地把噪聲看作加性噪聲,圖像序列可用下面的模型來表示:
x(i,j,t)=hδ(i-it,j-jk,t)+fn(i,j,t)+(i,j,t) (1)
這里目標被看作位于點(it,jt)處幅度為h的沖激函數,圖像預處理就是對1/f噪聲fn(i,j)去相關.實際上,1/f噪聲是一種統計自相似的分形隨機過程[1].小波變換方法能夠刻劃分形過程的精細結構,對于非平穩過程的分析具有一定的優越性.因此本文采用這一方法對噪聲進行白化處理.
小波變換將信號在一個由小波函數ψ(t)的整數平移和尺度伸縮所構成的規范正交基上展開,對于信號x(t),它能夠用小波正交基來表示,同時還可由其小波變換系數來恢復:
xmn=∫+∞-∞x(t)ψmn(t)dt (2)![]() (3)
(3)
{xmn}即為x(t)在平移伸縮系{ψmn(t)}上的小波變換,對于二進小波變換,小波基函數可表示為:
ψmn(t)=2m/2ψ(2mt-n) (4)
文獻[1]中提出了一種基于小波變換的1/f噪聲表示方法,并證明了1/f噪聲的小波變換系數可近似地看作彼此互不相關,通過各個尺度上方差的規一化,就能夠對1/f噪聲進行白化.對于1/f噪聲信號x(t),其小波變換系數的方差具有如下形式:
Var[xmn]=σ22-γm (5)
其中γ為1/f噪聲的功率譜參數.由于小波變換系數近似互不相關,小波變換系數可以用下式表示:
xmn=[σ2-γm/2]υmn (6)
其中小波變換系數υmn為零均值,單位方差并且互不相關的隨機變量,它對應著一個平穩的白噪聲υ(t),如果用(σ2-γm/2)-1對xmn歸一化,就能夠通過重構方程(3)得到一個白化的隨機過程.
由于紅外線列掃描圖像只在掃描方向存在1/f噪聲,為減少計算量,只考慮掃描方向的白化,這樣可以只進行一維的處理,考慮到加性的白噪聲,線列掃描序列的小波變換系數的方差為:
Var(xmi,j)=σ22-γm+σ2 (7)
其中σ2為白噪聲的方差,經(σ22-γm+σ2)-1/2對小波變換系數xmi,j尺度化后,再用式(3)進行信號重構,就能夠實現線列掃描方向的白化.通過上述的推導,可以得知預處理后的輸出為零均值,單位方差的白噪聲過程.
2.膨脹累加平均
當目標在幀間移動很小時,直接采用多幀圖像累加的方法可以有效地抑制噪聲,提高信噪比.但是幀間運動較大的點目標,直接累加并不能夠實現目標能量的有效積累.在本文中,首先對圖像進行膨脹運算,將目標由一個點膨脹成一個斑點,從而使得不同幀上的目標能量仍然能夠實現累加,起到目標增強的作用.結構函數g(x)對函數f(x)的膨脹運算記為![]() ,它可以由下式計算:
,它可以由下式計算:
![]() (8)
(8)
其中D(g)表示結構函數g(x)的定義域,進一步可以得到二維膨脹運算:
![]() (9)
(9)
本文選擇平頂形的結構函數,即對于所有(x,y)∈D(g),都有g(x,y)=1成立,此時某一個像素點的膨脹運算結果相當于以該點為原點的結構函數窗口內的所有像素灰度的最大值,則有:
![]() (10)
(10)
其中結構函數尺寸大小根據目標在幀間運動的大小來選取.累加平均后的圖像可表示為:
![]() (11)
(11)
其中N為累加幀數,經N幀累加平均后,目標點和噪聲點的均值保持不變,而均方差變為單幀時的1/N.最后將累加的結果取門限即得到一組目標候選點.
3.數據關聯與檢測判決
數據關聯采用最近鄰關聯方法將目標候選觀測點連成多條航跡.把每一次累加輸出后的目標候選點視為一組,在得到T組連續候選點后,如果某一個目標航跡中的觀測點數不少于S個,判決該航跡為目標航跡.假設第i條航跡觀測數為nc(i)個,檢測判決即為如下的判決過程:
![]() (12)
(12)
三、模擬實驗結果
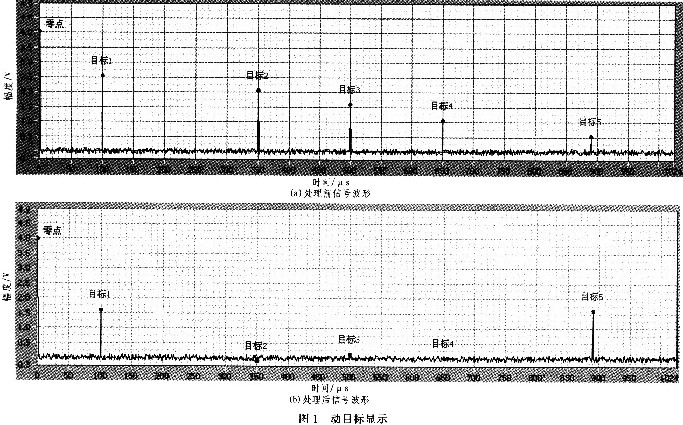
圖(1)給出了原始的紅外線列掃描圖像,從圖像中可以看到圖像在列方向(掃描方向)具有很強的相關性.圖(2)為經小波變換預處理后的圖像,圖像列方向上的相關性得以濾除,圖(3)為圖像經膨脹累加取平均的結果,從中可以看到目標得到增強,圖(6)為最終檢測判決結果.實驗證明該算法能夠有效地檢測出信噪比為2的運動點目標.


|
圖1 紅外線列掃描圖像 |
圖2 經預處理后的圖像 |


|
圖3 膨脹累加平均后的圖像 |
圖4 閾值化后的圖像 |


|
圖5 候選點航跡 |
圖6 檢測結果(目標航跡 |
| 四、算法檢測性能分析 首先假定噪聲是均值為零,方差為σ2的高斯白噪聲.為分析方便起見,假定目標為能量固定的沖激信號,幅度為m,令p0(x)和p1(x)分別表示噪聲點和目標點灰度的概率密度函數
并令噪聲點和目標點灰度值的分布函數分別為P0(x)和P1(x).下面討論fd(x,y)中像素灰度的概率密度函數.由概率論的知識可知,兩個相互獨立的隨機變量的最大值的分布函數為兩個分布函數之乘積.令膨脹窗口的面積為M,如果某一個像素點的膨脹窗口內不包含目標點,則膨脹運算后該點灰度的分布函數為: Pd,0(x)=PM0(x) (14) 對式(14)求導數,得到: Pd,0(x)=Mp0(x)PM-10(x) (15) 同樣可以得到像素點的膨脹窗口內包含有目標點時,膨脹運算后該像素的灰度概率分布函數和概率密度函數分別為: Pd,1(x)=P1(x)PM-10(x) (16) 實際上,累加平均的過程可以看作先將fd(x,y,k)除以N,再進行相加的過程.假定幀間沒有相關性,我們知道,相互獨立隨機變量之和的概率密度函數為隨機變量的概率密度函數之卷積.則累加平均后,噪聲點和目標點的灰度概率密度函數為N次自卷積的結果:
從上式可以看出,膨脹累加平均后的灰度概率密度函數的表達式十分復雜.本文采用近似方法計算pa,0(x)和pa,1(x),令膨脹累加后目標點和噪聲點的灰度分別為高斯分布N(μ1,σ21)和N(μ0,σ20),對于累加平均判決門限Ts,其相應的檢測概率PD,a和虛警概率PF,a為
這里Φ[.]為標準正態分布的分布函數. μ0=σμmax(M) 這里μmax(M)和σ2max(M)為M個相互獨立且服從標準正態分布的隨機變量的最大值的均值和方差 μmax(M)=∫∞-∞Mxφ(x)ΦM-1(x)dx (21) 對于目標點,通過概率密度函數pa,1(x)計算目標點處膨脹運算后的均值和方差是不容易的.將目標膨脹窗口內的像素點的灰度寫成{x1,x2,…,xM}的形式,不妨假設x1為目標點的灰度,則 max{x1,x2,…,xM}=max{x1,max{x2,…,xM}} (23) 令xm=max{x2,…,xM},由式(20)可知,xm的均值和方差為σμmax(M-1)和σ2σ2max(M-1).則目標點的均值和方差可表示為: μ1=E[max(x1,xm)] 文獻[4]中給出了一種計算兩個正態分布的隨機變量的最大值的均值和方差的計算方法,我們直接引用它來計算μ1和σ21:
其中
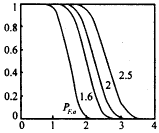
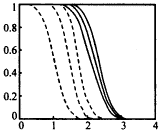
在圖(7)中給出了背景噪聲為零均值單位方差的白噪聲、膨脹窗口取為2×2時PF,a和不同信噪比條件下PD,a隨分割閾值的變化曲線.圖(8)為信噪比取2、選取不同尺寸的膨脹窗口時(w×w),檢測概率PD,a和虛警概率PF,a隨分割閾值的變化曲線.從中可以看出,PD,a隨膨脹窗口大小的變化并不明顯,而PF,a則隨著膨脹窗口的增大而迅速增加.因此選取的窗口太大,會降低檢測性能. |
|
圖7 PF,a和PD,a隨分割閾值Ts的關系曲線(曲線附近的數字表明信噪比) |
圖8 SNR=2時不同的膨脹窗口下的PF,a和PD,a(虛線表示PF,a,實線表示PD,a; |
| 下面討論關聯后的檢測性能.設膨脹累加門限化后的虛警概率為PF,a,目標檢測概率為PD,a,航跡關聯窗口取為[-nK,nK]×[-nK,nK],令K=(2nK+1)2,則對于虛警航跡,在關聯窗口內有后續觀測的概率為:
Pz,0=1-(1-PF,a)K (27) 由上式可以看出,虛警概率PF,a不宜取得較大,因為這樣將會使虛警點在關聯窗口內獲得后續觀測,從而增加整個檢測算法的虛警概率.由于不同幀間的觀測是相互獨立的,因此航跡中的檢測點的數目服從二項分布,包含t個檢測點的航跡發生的概率為
考慮檢測概率的計算.由于目標可能被分割出來,也有可能被閾值化為零,因此目標航跡的后續檢測點可能為點目標,也有可能為關聯窗口內的虛警點,仿照式(27),可得窗口內除點目標以外其余(K-1)個噪聲點非零的概率為: Pz,0,K-1=1-(1-PF,a)K-1 (29) 此時點目標的檢測點-航跡關聯,會有四種情況發生 Pz,1=PD,a+(1-PD,a)Pz,0,K-1 (30) 目標檢測概率為:
航跡正確關聯包括前兩種情況,因此航跡正確檢測的概率,即不包含噪聲點的航跡檢測概率為:
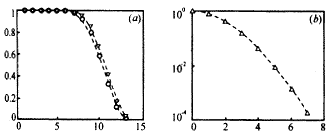
對SNR=2,N=5,膨脹窗口取為2×2,關聯窗口為5×5時,在不同的PF,a值條件下,整個算法的檢測概率PD和虛警概率PF與航跡判決閾值S之間的關系進行了分析計算(限于篇幅,不一一給出).發現PF,a的值取在0.002和0.005之間比較合適.這樣選擇主要出于兩方面的考慮:一是此時檢測概率和航跡正確概率很接近,更重要的是此時具有較高概率PD,a,這對于航跡的正確關聯是十分重要的.圖(9)給出了當PF,a=0.005、T=12時,整個算法的檢測概率PD、PT和虛警概率PF與航跡判決閾值S之間的關系. |
|
圖9 PF,a=0.005時的檢測概率和虛警概率 (a)三角點線表示PD,圓點線表示PT;(b)虛警概率PF 五、總 結 |
 電子發燒友App
電子發燒友App






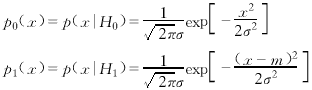 (13)
(13)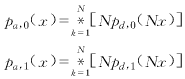 (18)
(18)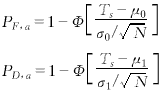 (19)
(19)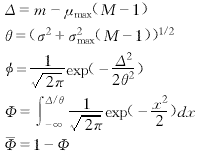 (26)
(26)















評論