其大致步驟如下：

　　(1)將輸入自變量作為橫坐標(biāo)，輸出量即測試值作為縱坐標(biāo)，描繪出測試曲線。

　　(2)對所描繪的曲線進(jìn)行分析，確定公式的基本形式。如果數(shù)據(jù)點基本成一條直線，則可以用一元線性回歸方法確定直線坐標(biāo)。如果數(shù)據(jù)點描繪的是曲線，則要根據(jù)曲線的特點判斷曲線屬于何種函數(shù)類型。可對比已知的數(shù)學(xué)函數(shù)曲線加以對比、區(qū)分。如果測試曲線很難判斷屬于何種類型，則可以按多項式回歸處理。

　　(3)確定擬合方程中的常量。可根據(jù)一系列測試數(shù)據(jù)確定方程中的常量。

　　(4)檢驗所確定的方程穩(wěn)定性和顯著性，用測試數(shù)據(jù)中的自變量代入擬合方程計算出函數(shù)值，看與實際測試值是否一致。差別的大小通常用標(biāo)準(zhǔn)差來表示，進(jìn)行方差分析，F(xiàn)檢驗等。如果所確定的公式基本形式有錯誤，此時應(yīng)建立另外形式的公式。

　　在進(jìn)行研究分析的時候，考慮某功率放大器放大倍數(shù)的變化情況。假設(shè)經(jīng)過數(shù)據(jù)統(tǒng)計得到此功率放大器的放大倍數(shù)情況如表1所示。

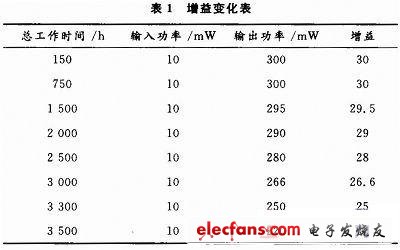
　　2.2 建模與仿真

　　根據(jù)表1所給的數(shù)據(jù)，運用回歸分析的方法對放大器的增益參數(shù)進(jìn)行建模，在置信水平為95%的條件下按照回歸分析的步驟得到其隨工作時間的變化曲線，如圖2所示。

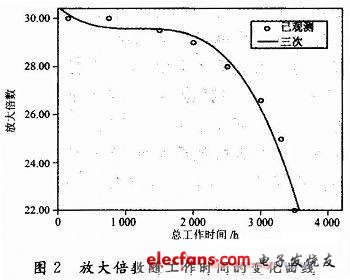
　　由圖2可以看出當(dāng)用三次多項式作為其數(shù)據(jù)模型時能比較好的擬合所給的數(shù)據(jù)，對其進(jìn)行參數(shù)估計和模型匯總得到各參數(shù)的基本情況如表2所示。

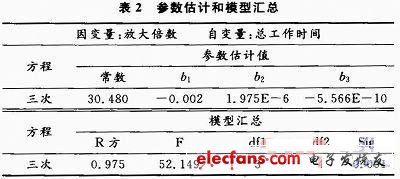
　　根據(jù)表2的數(shù)據(jù)及F檢驗法的判斷標(biāo)準(zhǔn)可知此方程回歸效果顯著，由此可根據(jù)此方程得到因變量增益的預(yù)測值和置信區(qū)間，具體數(shù)據(jù)如表3所示。

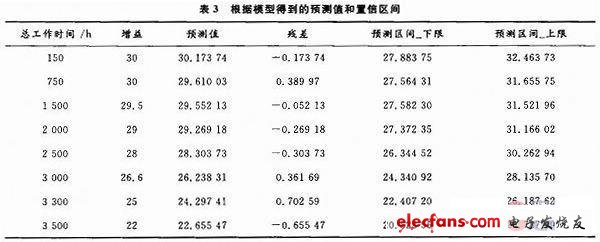
　　3 結(jié)語

　　回歸模型是分析測試數(shù)據(jù)很重要的工具，可以得出的是參數(shù)之間的變化關(guān)系，也許單獨某對參數(shù)之間的變化關(guān)系不足以提供有意義的信息，還可以建立多元回歸模型來研究多個參數(shù)和某個參數(shù)之間的變化關(guān)系。由于回歸分析在非線性分析中的局限性，在以后的工作中將著重研究人工神經(jīng)網(wǎng)絡(luò)在此方面的應(yīng)用。參數(shù)模型建立的方法并不是固定的，隨著研究點的不同，模型的選擇也不同。通過所建立模型，可以不需要進(jìn)行實際測量來預(yù)測電子系統(tǒng)未來的電磁兼容狀況，有效指導(dǎo)系統(tǒng)的電磁兼容性分析和保障。