濾波器越長越好？我們身處的時代崇尚“越大越好”，但這一至理名言也許并不適用于FIR濾波器長度。

DSP支持的濾波器長度通常為1024點（tabs），有些高達4096點。為什么人們不想要或不需要長度更長的FIR濾波器？如果生廠商在DSP中引入8192點的FIR濾波器，人們會舍棄競爭產品而選擇它嗎？

頻率越低，時間越長

首先，我們需要一份用于練習和實驗的文件。可使用揚聲器的測量數據，但稍微簡單的文件更易于幫助我們發現重要的點。

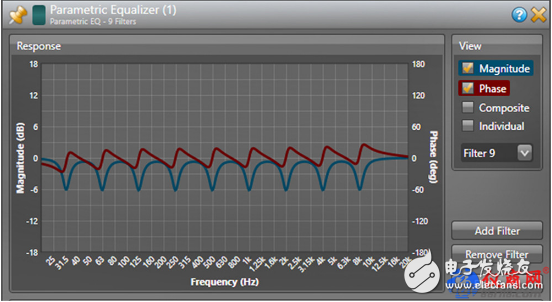
請查看圖1作為參考。我在FIRCapture軟件中創建該系列提升濾波器（分離的以一個倍頻程為帶寬的對稱均衡器）并保存為WAV文件。可通過任何9段參量均衡器輕松創建此響應。

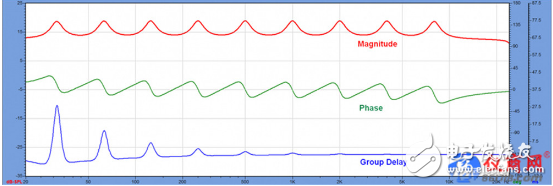
我選擇Q=6以最大化減少濾波器之間的重疊。這一組濾波器又構成了一個濾波器，它與揚聲器的響應并無二致，更別提在最高頻和最低頻處必不可少的高通和低通響應了。如果這就是一個揚聲器的響應（讓我們假設如此），我們將希望對凸起部分進行均衡處理，以獲得整體較為平坦的響應。通過該文件，我們可以很好地考察FIR濾波器的頻率解析度。

頻域視圖顯示頻率響應的振幅、相位和群延時。請注意，相位和群延時是兩種不同的方式，顯示信號通過時，濾波器如何改變其時間行為。由于相位是相對的，因此每個凸起的相位行為都相同。

在之前的文章中我演示過，一個帶通濾波器的最小相位響應首先呈正向，然后在濾波器的中心頻率回到原點，最后為負向。這個相位偏移將使得通過濾波器的信號產生與頻率相關的振鈴現象（Ringing）。振鈴現象持續的時間由群延時圖顯示。

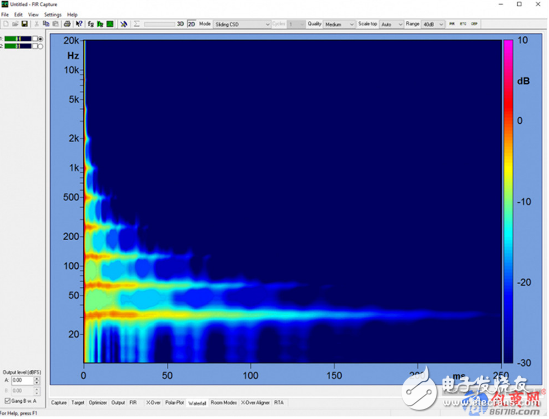
圖2是該濾波器的頻域/時域綜合圖。圖3顯示了每個分離倍頻程的中心頻率的波長。二者有何相關？由于聲速約為1英尺/毫秒（ft/ms），每個倍頻程的中心頻率波長大約等同于一周期所需時間。波長的概念以十分形象的方式顯示聲波與時間和空間有關，而濾波器的響應也是如此。

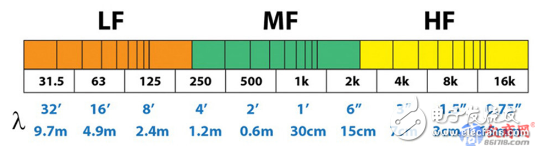
群延時（GD）與濾波器的頻率波長成正比關系，頻率越低，群延時越長。單從名稱來看，似乎指的是信號通過濾波器所造成的延時，這有點誤導人。濾波器的儲存屬性造成了振鈴現象，即信號中增加了多余周期。

群延時顯示了提升濾波器占據的時長。低頻凸起具有很長的振鈴，這不足為奇。群延時與濾波器頻率成反比（與波長成正比），相位偏移相等時，頻率越低，群延時越長。

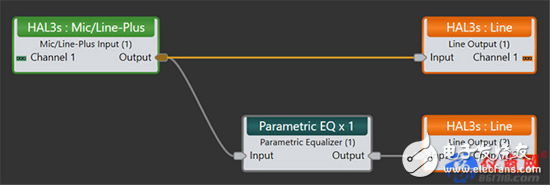
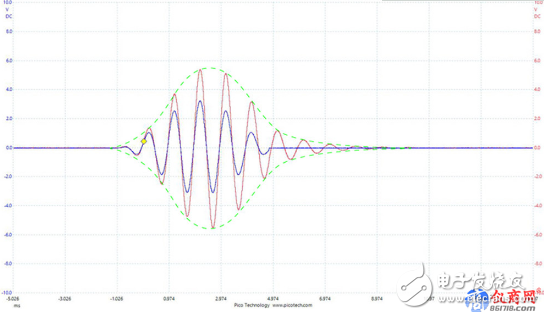
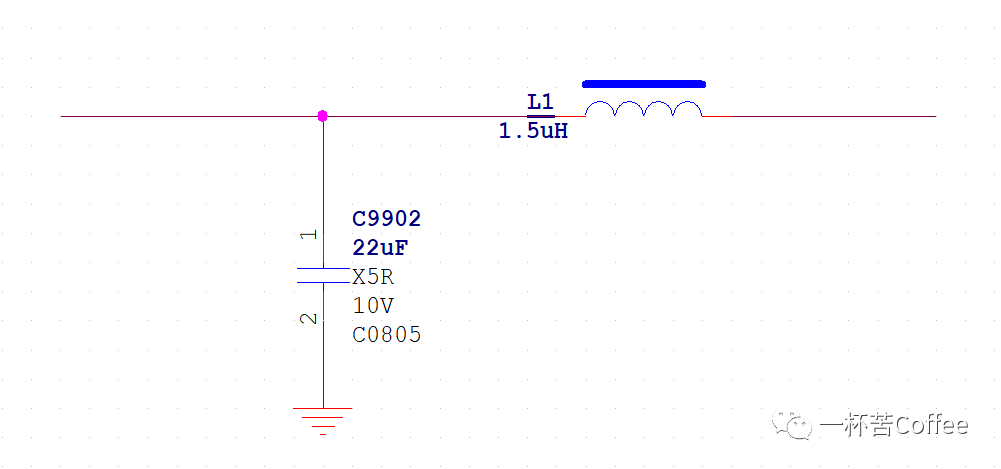
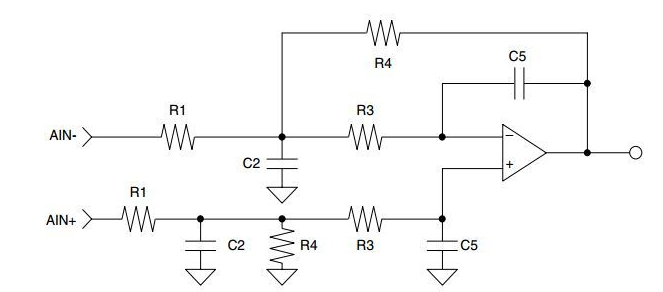
為方便演示，我們以圖4所示的信號處理鏈路為例。我們輸入一個測試信號，看看將發生什么。圖5為2通道示波器顯示的結果。藍色軌跡為1000Hz 6.5周期的小波。這是Don Keele測試信號中的一個。紅色軌跡為此信號通過一個1000 Hz提升濾波器之后的結果。請注意，原信號和通過濾波處理的信號相位一致，但是經過濾波器的信號周期增加了。這是在時域觀察的振鈴現象。一個削減濾波器的振鈴現象將占據同等時長。

IIR均衡

一個模擬或數字無線脈沖響應濾波器（IIR filter）如何校正響應？必須是產生與凸起相反的振幅響應和相位偏移。由于IIR濾波器是循環的，即利用反饋將一部分輸出信號返回到輸入端進行再處理（可類比電容的充電和放電）。

因此，IIR濾波器在操作過程中沒有低頻限制（起碼與FIR濾波器相比時如此），而且不會造成大量處理延時。只要有輸入信號，就會有輸出信號，濾波器的脈沖響應（理論上）永遠不會衰減到零。

正向群延時是窄頻段提升濾波器的標志（圖1），而負向群延時是削減濾波器的標志。圖7顯示了通過一款受歡迎的DSP的EQ模塊實現的一組IIR濾波器。通過對比圖1每個凸起以及圖7每個陷波的振幅以及相位，可以發現圖7的均衡器可以完全校正我文件的響應。

順便提一句，窄頻段信號的群延時并不代表信號延時，而顯示了濾波器振鈴現象所占的時長。音頻中有些術語并非字面上的含義，比如“恒定電壓”（Constant voltage），但這是另外一個話題，這里不再贅述。

最小相位FIR EQ

下面讓我們討論最小相位FIR。它的響應可以和參量均衡器生成的IIR濾波器一模一樣。關鍵的區別在于FIR濾波器的響應與驅動信號完全無關。它是有限長度的脈沖響應，頻率解析度與長度相關。

由于T = 1/F，要影響的頻率越低，需要的濾波器長度越長（時間跨度，更多點位數）。對低頻凸起進行校正需要在每一個頻率引入振幅和相位的共軛，這也會與群延時共軛。對于低頻凸起而言，這是非常長的時間跨度。

再看回圖1。由于該濾波器是最小相位濾波器，因此處理延時很小，與IIR濾波器的差不多。差別在于FIR濾波器的帶寬由它的長度決定（圖6），因此需要一個長度非常長的濾波器對低頻凸起進行均衡處理。這與創建濾波器所采用的處理算法無關。

頻率解析度

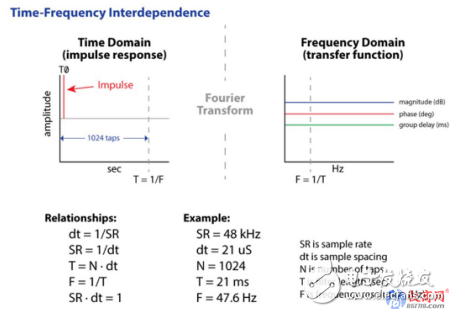
從圖6中可看出，一個1024點、采樣率為48 kHz的最小相位FIR濾波器，長度為21毫秒。由于T=1/F，此濾波器的頻率解析度為47.6 Hz。

這意味這什么？這意味著在頻域視圖下，每個數據點之間的間隔。

它同時也表示濾波器能影響的最低頻率。而事實上的頻率解析度還要低一些（能影響的最低頻率還要稍高一些），因為往往需要幾個周期的波形才能確定某一頻率。

要是增加更多點位呢？濾波器長度加倍將使得頻率解析度加倍，使得數據點之間的頻率間隔變成24 Hz。

它還使得低頻限制下潛一半，去到24Hz。這一趨勢將繼續，點位數每加倍，將使得濾波器的響應下潛一個倍頻程。因此，長度更長的FIR濾波器將使得：1） 濾波器擴展至更低頻率。2）濾波器的頻率響應呈現更多細節，因為數據點更加密集。

在最小相位FIR濾波器這種情況下，更多點位數大有裨益，因為這意味著濾波器可以擴展至更低頻率。由于這是最小相位濾波器，因此相比IIR濾波器并沒有增加額外的處理延時。要使我的示范文件獲得平滑的響應，大約需要4096點，這遠超過現有DSP能支持的點位數，這使得需要更多點位數的爭論愈演愈烈。

先別著急下結論

讓我們再認真考慮。最小相位FIR的行為與最小相位IIR濾波器一樣，只不過需要足夠多的點位數才能影響欲達到的最低頻率。低頻均衡需要更長的濾波器長度。

但是為什么要在DSP中通過占用大量系統資源的FIR濾波器模塊來創建一個最小相位濾波器呢？一個精心調節的參量均衡模塊（IIR）將占用少得多的系統資源，但產生同樣平滑的響應，且頻率解析度更佳（圖7）。使用盡可能少的系統資源得到所需結果，在音頻行業是最佳實踐，而使用FIR濾波器進行最小相位均衡并不高效，

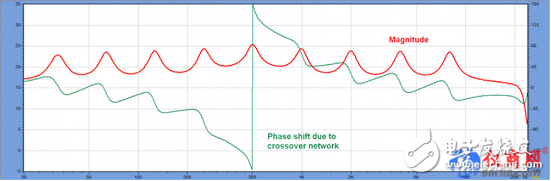
接下來讓我們思考校正的響應不是最小相位的這種情況。我在參考文件中，將一個二階全通濾波器（500 Hz）添加至響應中（圖8）。這將在濾波器的整個帶寬中造成相位偏移，但是對振幅響應的影響最小。在事實應用中，這種全通行為可能源于使用了分頻網絡。最小相位FIR濾波器不能補償這樣的額外的相位偏移。

線性相位FIR

一個線性相位FIR具有對稱的脈沖響應，主信號到達時間位于脈沖響應（IR）的中間（圖9）。我們將到達峰值設為相對時間零，在此之前的時間跨度提供了“負時間”到達，用于共軛主到達峰值之后的能量到達。

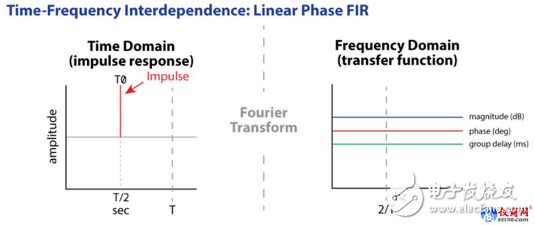
這些“預延時”與事實時間之間存在因果關系，但是與主要的信息到達時間沒有因果關系。這允許濾波器通過相反的“負時間”響應對反射能量進行補償。

所以，如果點位長度為1024個點，線性相位FIR濾波器將把主到達時間置于T/2處，讓一半濾波器長度提供預到達時間，以共軛揚聲器或房間產生的后到達能量。它還允許引入所需的負向群延時，以補償分頻器的全通響應。

因為將一半的濾波器長度用于“負時間”校正，濾波器的頻率解析度將減半。例如，1024點的最小相位FIR濾波器頻率解析度為47.6 Hz。而同樣長度的線性相位FIR濾波器頻率解析度為95.2 Hz，因為預留了一半長度用于相位均衡。

點位數越多越好？

對于最小相位FIR濾波器而言，似乎如此。問題在于非最小相位濾波器需要預留一半長度用于相位均衡。這會表現為處理延時（常錯誤地被稱為延遲）。與最小相位FIR濾波器不同，隨著線性相位FIR濾波器的長度增加以提高其頻率解析度，它的延時也會增長。這不是由DSP的速度造成，而源于TF = 1。

現在再調出我的參考文件，只不過這次是一系列的削減濾波器，削減的頻率與原有提升濾波器（圖10）一致。從之前的討論中得知，群延時視圖（藍線）顯示濾波器振鈴現象的時間長度。請注意，它現在呈負向，但這僅意味著這個濾波器產生的相位偏移在整個帶寬不斷擴大。并不表示出現了“時間提前”或者濾波器的響應是非因果關系的。

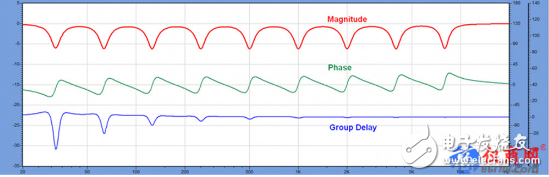
無法回避的是，頻率越低，濾波器發揮影響需要的時間越長，在最低倍頻程的中心頻率（31.5 Hz）這個時間將變得非常長（~40 ms）。對于現場演出和許多固定安裝應用來說，這么長時間的處理延時是不可接受的。一個1024點的FIR濾波器（48 kHz采樣率）時長為21毫秒，意味著處理延時大約為10.5毫秒。

將采樣率提升至96 kHz并不會降低處理延時，因為必須處理的采樣數量也加倍了。無法改變的事實是，21毫秒的長度最低僅可以影響48Hz，而事實上的頻率解析度是48Hz的3倍，或者說是150 Hz。

問題變得更糟糕

線性相位FIR濾波器還有另一個缺點。由于“相對時間零”位于濾波器時長的中間，其頻率解析度是最小相位FIR濾波器的一半。

因此，如果一個1024點的最小相位FIR濾波器最低可以影響150Hz，那么一個1024點的線性相位FIR濾波器最低只可以影響300Hz。

影響的頻率要下潛至150Hz將需要一個2048點的濾波器，意味著處理延時也要從10.7毫秒翻倍到21毫秒。

而針對我的示范文件，將需要一個8196點的FIR濾波器才能使整個通帶的響應變得平滑。所需的處理延時約為85毫秒。

表面來看，FIR濾波器的長度越長，好處似乎是可以提高頻率解析度，從而：1）影響更低頻率。2）在整個帶寬包含更多細節。

我已經向大家展示，至少對于線性相位FIR濾波器而言，要影響更低頻率（更多點位數）將提高處理延時。這不是因為處理能力不足而造成，而源于時間和頻率的相關性。低頻持續較長時間，而且占據大量空間。數字處理無法改變此現狀。

部分好處

在可聽頻譜內一共有10個倍頻程，所以每個倍頻程占據整體的十分之一（對數標尺）。濾波器長度加倍，將使得處理延時加倍，而這僅僅使得你均衡處理的頻譜多了十分之一。

就好比讓功放的功率加倍只為了得到3dB提升一樣，有時到了一個臨界點，得到的回報很少，根本就不值得。在功放的例子中代價是金錢，而對線性相位FIR濾波器而言，代價是延時。可以說，數字處理的貨幣就是時間。你可以得到很好的效果，前提是可以等待足夠長時間。

在大多數房間中，最低的兩個倍頻程（次低頻）位于施洛德頻率曲線（Schroder Frequency）下方，這時房間模式（room modes）對每個座位的頻率響應有深刻影響。即便我們通過線性相位FIR濾波器，將房間中某一點的響應處理得非常“完美”，在其它座位響應也是不一樣的，這樣做的意義何在？

那需要更高的濾波器精度嗎？一個1024點的濾波器，數據點之間的頻率間隔約為48Hz。如果這還不夠校正你的頻率響應，很可能你在嘗試校正一些根本不應該訴諸均衡處理的東西，比如由于房間反射造成的梳狀濾波。頻率響應中的“細節”越多，則時間響應越多與“位置相關”，因為這些細節由從不同表面而來的反射造成。

移動測試話筒，則響應發生很大改變。一個精度很高的FIR濾波器只適合“校正”空間中的一個點。這可能適用于在特定的話筒位置對會議系統進行回聲消除，但這無益于整個觀眾區。更長的FIR濾波器對現場應用并沒有太大意義。

更高采樣率是否有幫助？

純屬坊間傳言。很遺憾并非如此。再回到圖6，濾波器點位的時間間隔dt=1/SR（采樣率），乘以點位數（N）可以得到濾波器的時間長度（T）。頻率解析度（F）為1/T。

這是簡單的關系，顯示了如果采樣率加倍，濾波器的頻率解析度將降低一半。我們把問題弄得更糟了！如果采樣率加倍，那么需要處理的采樣數量要乘以2，這樣必須要使得濾波器長度加倍，才能保持同樣的頻率解析度。

讓我們考察相反的情況。采樣率減半將提高濾波器的頻率解析度。但是要犧牲高頻響應，只能擴展至SR/2。奈奎斯特采樣定理（Nyquist-Shannon）是不能否定的。

這一切都不能改變線性相位FIR濾波器所需的處理延時，即濾波器時長的一半。更高（更低）的采樣率不能改變信號的時間、頻率或波長。

結論

毫無疑問，隨著技術的發展我們將來會擁有更長的數字濾波器。芯片不斷完善，使用芯片的產品也如此。我們可能還記得16 bit/44.1 kHz的“CD級”音頻曾經都是幾乎不可能實現的。但是如今很多人都認為它解析度很低。FIR濾波器也將沿著這樣的軌跡發展。

但是實現更長的濾波器還會遇到一些障礙，而這與技術無關。我在上面的文章中已顯示，最主要的障礙是處理延時，這由濾波器必須影響的時間長度有關（見圖1）。

在現場音響系統中，我們只能容忍一點延時。這個標準不是很精確，但是大部分人會同意超過20毫秒的濾波處理是比較長的時間。這一不可避免的處理延時會增加信號鏈中其它數字設備的延遲，一般會額外增加10毫秒。處于時間考慮，我們不得不放棄對低頻進行線性相位均衡處理，至少對現場應用如此。

對高頻應用線性相位FIR濾波器，對低頻應用最小相位FIR濾波器似乎是一種解決方法。這被稱為“混合相位”濾波器，我認為，這將是未來的發展趨勢。有些人開始認為IIR濾波器無用武之地了，但是不可否認，它們有最寬的帶寬、最低的處理延時而且使用的系統資源比其它任何數字濾波器都要少。請不要拿走我的參量均衡器模塊！

點位數量不能無限度多，意味著我們必須思考校正的重點是什么及其背后的理由。就好比罐子里只剩下一勺花生醬時，我們要好好利用。我的均衡處理如何影響揚聲器的整個覆蓋區域，而不僅限于測試話筒所擺放的“黃金位置”？要是考慮多個座位的情況，那線性相位FIR濾波器的魔法光環會迅速褪去。

好好運用一個1024點的FIR濾波器，比稀里糊涂使用一個長度更長的濾波器要好。人類認知為模數轉換所需的采樣率和位深設置了合理限制，時間、頻率、波長和延遲也限制了更長FIR濾波器所能帶來的好處。在音頻行業，把東西弄得更大總是值得商榷，數字濾波器也不例外。這也并非壞事，可以保持平衡，并且促使人們思考是追求真正產生好聲音，還是規格參數表的數據更好看。

這又詮釋了“少即是多”。