問:有關運算放大器的噪聲我應該知道些什么?
答:首先,必須注意到運算放大器及其電路中元器件本身產生的噪聲與外界干擾?或無用信號并且在放大器的某一端產生的電壓或電流噪聲或其相關電路產生的噪?聲之間的區(qū)別。?
干擾可以表現為尖峰、階躍、正弦波或隨機噪聲而且干擾源到處都存在:機?械、靠近電?源線、射頻發(fā)送器與接收器、計算機及同一設備的內部電路(例如,數字電路或開關電源)。?認識干擾,防止干擾在你的電路附近出現,知道它是如何進來的并且如何消除它或者找到對?付干擾的方法是一個很大的題目。
如果所有的干擾都被消除,那么還存在與運算放大器及其阻性電路有關的隨機噪聲。它?構成運算放大器的控制分辨能力的終極限制。我們下面的討論就從這個題目開始。
問:好,那就請你講一下有關運算放大器的隨機噪聲。它是怎么產生的?
答:在運算放大器的輸出端出現的噪聲用電壓噪聲來度量。但是電壓噪聲源和電?流噪聲源都能產生噪聲。運算放大器所有內部噪聲源通常都折合到輸入端,即看作與理想的?無噪聲放大器的兩個輸入端相串聯或并聯不相關或獨立的隨機噪聲發(fā)生器。我們認為運算放?大器噪聲有三個基本來源:
·一個噪聲電壓發(fā)生器(類似失調電壓,通常表現為同相輸入端串聯)。
·兩個噪聲電流發(fā)生器(類似偏置電流,通過兩個差分輸入端排出電流)。?
·電阻噪聲發(fā)生器(如果運算放大器電路中存在任何電阻,它們也會產生噪聲。?可把這種噪聲看作來自電流源或電壓源,不論哪種形式在給定電路中都很常見)。
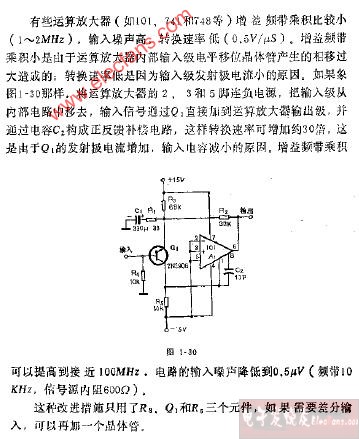
運算放大器的電壓噪聲可低至3?nV/Hz。電壓噪聲是通常比較強調的一項技?術指?標,但是在阻抗很高的情況下電流噪聲常常是系統噪聲性能的限制因素。這種情況類似于失?調,失調電壓常常要對輸出失調負責,但是偏置電流卻有真正的責任。雙極型運算放大器?的電壓噪聲比傳統的FET運算放大器低,雖然有這個優(yōu)點,但實際上電流噪聲仍然比較大。?現在的FET運算放大器在保持低電流噪聲的同時,又可達到雙極型運算放大器的電壓噪聲水?平?。
問:電壓噪聲達到3?nV/Hz的單位是怎么來的?它的含?義如何?
答:讓我們討論一下隨機噪聲。在實際應用中(即在設計者關心的帶寬內)許多噪?聲源都屬于白噪聲和高斯噪聲。白噪聲是指在給定帶寬內噪聲功率與頻率無關的噪聲。?高斯噪聲是指噪聲指定幅度X出現的概率服從高斯分布的噪聲。高斯噪聲具有這樣的特性:?當?來自兩個以上的噪聲有效值(rms)進行合成時,而且提供的這些噪聲源都是不相關的(即一種?噪聲信號不能轉換為另一種噪聲信號),這樣合成的總噪聲不是這些噪聲的算術和而是它們?平?方和的平方根(rss)(這意味著噪聲功率線性疊加,即平方和相加)。例如有三個噪聲源V?1,V2和V3,它的rms和為:
V0=V21+V22+V23
由于噪聲信號的不同頻率分量是不相關的,從而rss合成結果是:如果單位帶寬(brick??wall?bandwidth)為Δf的白噪聲為V,那么帶寬為2Δf的噪聲為V2+V2=?2V。更為普遍的情況,如果我們用系數K乘以單位帶寬,那么KΔf帶寬的噪?聲為KV。因此在任何頻率范圍內將Δf=1Hz帶寬的噪聲有效值所定義的函數?稱?作(電壓或電流)噪聲譜密度函數,單位為nV/Hz或pA/Hz。對于白噪聲?,噪聲譜密度是一個常數,用帶寬的平方根乘以譜密度便可得到總有效值噪聲。
有關rss和的一個有用結果是:如果有兩個噪聲源都對系統噪聲有貢獻,而且一個比另?一個大3或4倍,那么其中較小的那個常常被忽略,因為
42=16=4,但是42+12=1?7=4?12
兩者之差小3%,或0?26?dB。
32=9=3,但是32+12=1?0=3?16
兩者之差小6%,或0?5?dB。
因此較大的噪聲源對噪聲起主要作用。
問:那么電流噪聲又如何呢?
答:簡單(即不帶偏置電流補償)的雙極型和JFET運算放大器的電流噪聲通常在偏?置?電流的散粒噪聲(有時稱為肖特基噪聲)的1或2?dB范圍以內。在產品說明中一般不給出。散?粒噪?聲是由于電荷載流子隨機分布以電流形式通過PN結引起的電流噪聲。如果流過的電流為I,?那么在帶寬B內的散粒噪聲In可用下述公式來計算:
In=2IqB
其中q為電子電荷(1?6×10?-19?C)。應當注意2Iq為噪聲譜密度,即?這種噪聲為白噪聲。
從而告訴我們,簡單雙極型運算放大器的電流噪聲譜密度在Ib=200?nA時大約為250?f?A/Hz,而且隨溫度變化不大,而JFET輸入運算放大器的電流噪聲譜密度比較?低(在Ib=50?pA時為4?fA/Hz),并且溫度每增加20?°C其噪聲譜密度加倍?,因為溫度每增加10?°C其偏置電流加倍。
帶偏置電流補償的運算放大器的實際電流噪聲比根據其輸入電流預測的電流噪聲要大得?多?。理由是其凈偏置電流是輸入偏置電流與補償電流源之差,而其噪聲電流是從這兩個噪聲電?流的rss和導出的。
具有平衡輸入的傳統的電壓反饋運算放大器,其同相輸入與反相輸入端的電流噪聲總?相等(但不相關)。而電流反饋或跨導運算放大器在兩個輸入端具有不同的輸入結構,所以?其電流噪聲也不同。有關這兩種運算放大器兩個輸入端電流噪聲的詳細情況請參考其產品說?明。
運算放大器的噪聲服從高斯分布,在很寬的頻帶范圍內具有恒定的譜密度,或“白”噪?聲,但當頻率降低時,譜密度以3?dB/倍頻程開始上升。這種低頻噪聲特性稱作“1/f噪聲?”,因為這種噪聲功率譜密度與頻率成反比。它在對數坐標上斜率為-1(噪聲電壓或電流1/?f頻譜密度斜率為-1/2)。-3?dB/倍頻程譜密度直線延長線與中頻帶恒定譜密?度直線的交點所對應的頻率稱作1/f轉折頻率(corner?frequency),它是放大器的品質因數?。早期的單片集成運算放大器的1/f在500?Hz以上轉折,但當今的運算放器在20~50?Hz轉折?是常見的,最好的放大器(例如AD?OP?27和AD?OP?37)轉折頻率低到2?7?Hz。1/f噪聲?對于等比率的頻率間隔(如每倍頻程或每十倍頻程)具有相等的增量。
問:為什么你們不公布噪聲系數?
答:放大器的噪聲系數(NF)用來表示放大器噪聲與源電阻熱噪聲之比,單位為dB?,可用下式表示:
NF=20logVn(amp)+Vn(source)Vn(source)?
其中Vn(amp)表示放大器噪聲,Vn(source)表示源電阻熱噪聲。
NF對射頻放大器來說是一項很有用的技術指標,一般總是使用相同的源電阻(50或75?Ω?)來驅動射頻放大器,但當這項指標用于運算放大器時容易引起誤解,因為運算放大器在許?多不同應用中其源阻抗(不一定是阻性的)變化范圍很寬。
問:源阻抗對噪聲有何影響?
答:當溫度在絕對零度以上時所有電阻都是噪聲源,其噪聲隨電阻、溫度和帶寬?的增加而增加(隨后我們將討論基本電阻噪聲或熱噪聲)。電抗不產生噪聲,但噪聲電流通過?電抗將產生噪聲電壓。
如果我們從某一個源電阻驅動一個運算放大器,那么等效輸入噪聲將是該運算放大器?的噪聲電壓,源電阻產生的噪聲電壓和放大器的噪聲電流In流過源電阻產生的噪聲電壓的?rss和。如果源電阻很低,那么源電阻產生的噪聲電壓和放大器的噪聲電流通過源電阻產生?的噪聲電壓對總噪聲的貢獻不明顯。在這種情況下放大器輸入端的總噪聲只有運算放大器?的電壓?噪聲起主要作用。
如果源電阻很高,那么源電阻產生的熱噪聲對運算放大器的電壓噪聲和由電流噪聲引?起的電壓噪聲都起主要作用。但值得注意的是,由于熱噪聲只是隨電阻的平方根增加,而由?電流噪聲引起的噪聲電壓直接與輸入阻抗成正比,所以放大器的電流噪聲對于輸入阻抗足夠?高的情況下總是起主要作用。當放大器的電壓噪聲和電流噪聲都足夠高時,則不存在輸入電?阻為何值時熱噪聲起主要作用的問題。?
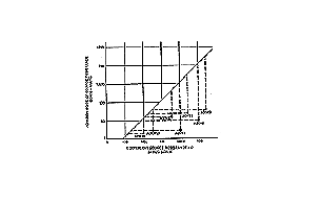
圖8?1?熱噪聲與源電阻的關系?
通過圖8.1來說明這一點,上圖給出了ADI公司的幾種典型運算放大器在某一源電阻范圍?內其電壓噪聲與電流噪聲的比較。圖中的對角線表示縱坐標熱噪聲與橫坐標源電阻之間的關?系。讓我們看一下圖中的AD?OP?27:水平線表示約為3?nV/Hz的電壓噪聲?對應小于500?Ω的源電阻。可以看出源阻抗減小100?Ω并沒有使噪聲減小,但源阻抗增加2?kΩ卻使噪聲增加。AD?OP?27的垂直線表示,當源電阻大約在100?kΩ以上的情況下,放大?器的電流噪聲產生的噪聲電壓將超過源電阻產生的熱噪聲,所以電流噪聲為主要噪聲源。?
應該記住,放大器同相輸入端的任何電阻都具有熱噪聲,并且又把電流噪聲轉換成噪聲?電壓。另外反饋電阻的熱噪聲在高電阻電路中非常突出。當評價運算放大器性能時所有可能?的噪聲源必須考慮。
問:請你介紹一下熱噪聲。
答:當溫度在絕對零度以上,由于電荷載流子的熱運動,所有電阻都具有噪聲,?這種噪聲稱為熱噪聲,又稱約翰遜噪聲。有時利用這種特性測量冷凍溫度。在溫度為T(開氏?溫度),帶寬為B?Hz,電阻為R?Ω的電壓噪聲Vn和電流噪聲In由下式計算:
Vn=4kTRB?和?In=4kTB/R
其中k為波爾茲曼常數(1.38×10?-23?J/K)。經驗規(guī)則表明,1?kΩ電阻在室溫下具有的?噪聲為4?nV/Hz。
電路中所有電阻產生的噪聲及其帶來的影響是總要考慮的問題。實際上,只有輸?入電路、反饋電路、高增益電路及前端電路的電阻才可能對總電路噪聲有上述明顯影響?。
一般可通過減小電阻或帶寬的方法減小噪聲,但降低溫度的方法通常沒有很大作用,除?非使電阻器的溫度非常低,因為噪聲功率與絕對溫度成正比,絕對溫度T=?°C+273°。
問:什么是“噪聲增益”?
答:到現在為止我們只討論了噪聲源,但還沒有討論出現噪聲電路的增益。人們?可能會想到,如果在放大器的指定輸入端的噪聲電壓為Vn并且該電路的信號增益為G,那?么輸出端的噪聲電壓應為GVn。但實際并非總是這樣。
現在請看圖8?2所示的基本運算放大器增益電路。如果運算放大器接成反相放大器(接B?端),?同相輸入端接地,將信號加到電阻Ri的自由端,那么這時增益為-Rf/Ri。反之,如果?運算放大器接成同相放大器(接A端),把信號加到同相輸入端,并且電阻Ri的自由端接地?,那么增益為(1+Rf/Ri)。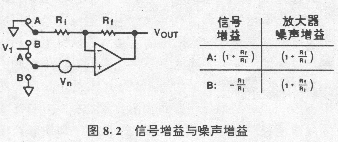
圖8?2?信號增益與噪聲增益?
放大器本身的電壓噪聲總是以同相放大器的方式被放大。所以當運算放大器接成信號增?益為?G的反相放大器時,其本身的電壓噪聲仍以噪聲增益(G+1)被放大。對于精密衰減的情況(G<?1),這種特性可能會出現疑問。這種情況一個常見的實例是有源濾波電路,其中阻帶增益可?能很小,但阻帶噪聲增益至少為1。
只有放大器輸入端產生的電壓噪聲和放大器同相輸入端電流噪聲流過該輸入端的任何阻?抗?所產生的噪聲(例如,偏置電流補償電阻產生的噪聲)才以噪聲增益被放大。而電阻Ri產?生的噪聲(不論是熱噪聲還是由反相輸入端噪聲電流引起的電壓噪聲)以與輸入信號相同的方?法被放大G倍,但反饋電阻Rf產生的熱噪聲電壓卻沒有被放大而以單位增益被緩沖送到輸?出端。
問:什么是“爆米花”噪聲?
答:在20多年前人們曾花了很大的精力研究這個“爆米花”噪聲(“popcorn”?no?is?e)問題,它是一種偶然出現的典型低頻噪聲,表現為失調電壓低幅度(隨機)跳變。當通過揚?聲器講話時,這種噪聲聽起來好像炒玉米花的聲,由此而得名。
在沒有形成集成電路工藝時,根本不存在這個問題,“爆米花”噪聲是由集成電路表面?工藝問題(如沾污)所致。當今對其產生原因已完全清楚,再不會有一個著名的運算放大器制?造廠家會出現因產生“爆米花”噪聲而成為用戶關心的主要問題。
問:峰峰噪聲電壓是使我能知道噪聲究竟是否有問題的最方便的方法。但是為什?么放大器制造廠家不愿用這種方法來規(guī)定噪聲呢?
答:正如前面所指出的,因為噪聲一般服從高斯分布。對于高斯分布來說,噪?聲最大值的說法是沒有意義的,即只要你等待足夠長的時間,理論上可超過任何值。另外,?實際上常用噪聲有效值這一概念。在某種程度上,它是一種不變量,即應用這種噪?聲的高斯概率分布曲線我們可以預測大于任何給定值噪聲的
表8?1?大于規(guī)定噪聲峰峰值概率
峰峰值?大于規(guī)定?峰峰值的概率
概率。假設給定噪聲源有效值為?V,由于噪聲電壓任何給定值的概率都服從高斯分布,所以可以得到:噪聲電壓大于2?V峰峰?值的概率為32%,大于3?V則為13%,依此類推,如表8?1所示。
如果我們使用噪聲峰峰值出現的概率來定義峰峰值,那么使可采用峰峰值這項技術指標?,但使用有效值更合適,因為它容易測量。當規(guī)定峰值噪聲電壓時,它常常為6?6倍有效?值(即6?6×rms),它出現的時間概率小于0?1%。
問:如何測量通常規(guī)定帶寬(0?1~10?Hz)范圍內低頻噪聲的有?效值?這一定要花費很長的時間。生產過程時間不是很寶貴的嗎??
答:時間確實很寶貴。雖然在表征器件的特性期間進行許多精細的測量是很必要?的,但以后在生產過程測量其有效值就不必花費那么多的時間。我們采用的方法是,在1/f?區(qū)域很低的頻率(低至0?1~10?Hz)范圍內,在1至3倍30?s周期范圍內測量其峰值,而且它?肯定?低于某個規(guī)定值。理論上這雖然不是令人滿意的好方法,因為某些好器件可能被排除,而?且?還有些噪聲會被漏檢,但實際上在可能做到的測試時間范圍內這是一種最好的方法。而且如?果它接近合適的閾值極限,那么這也是一種可接受的方法。從保守的眼光看來,這是測量噪?聲的?可靠方法。不符合最高等級標準的那些器件仍然可以按照符合這項指標等級的器件來銷售。?
問:你還遇到過運算放大器其它噪聲影響嗎?
答:有一種常遇到的噪聲影響,它通常表現為運算放大器噪聲產生的失碼現象。?這種嚴重影響可能是由于模數轉換器(ADC)的輸入阻抗調制引起的。下面看一下?這種影響是如何產生的。
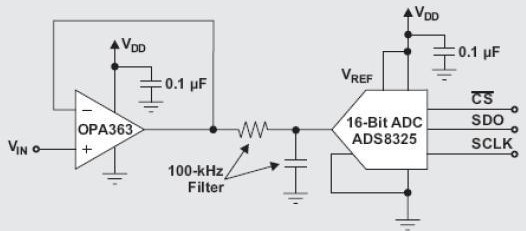
許多逐次逼近式ADC都有一定的輸入阻抗,它受轉換器時鐘的調制。如果用一種精密運算?放大器來驅動這種ADC,而且運算放大器的帶寬比時鐘頻率低得多,那么這個運算放大器便?不能產生充足的反饋為ADC的輸入端提供一個非常穩(wěn)定的電壓源,從而可能出現失碼。一般?地,當使用OP?07這類運算放大器來驅動AD574時就會出現這種問題。
解決這個問題的辦法是,使用頻帶足夠寬的運算放大器以便在ADC時鐘頻率影響下仍具有?低輸出阻抗,或者選用內部?含有輸入緩沖器的ADC,或者選用輸入阻抗不受其內部時鐘調制的ADC(許多采樣ADC都沒有這?個問題)。在運算放大器能夠穩(wěn)定地驅動容性負載,而且其系統帶寬減小?是不重要的情況下,在ADC輸入端加一個旁路去耦電容完全可以解決這個問題。
問:在高精密模擬電路中還有其它重要的噪聲現象嗎?
答:高精密電路隨時間漂移趨勢是一種類似噪聲現象(實際上可以證明,這種時間?漂移至少與1/f噪聲的低頻端是相同的)。當我們規(guī)定長期穩(wěn)定度時,通常以μV/1?000?h?或ppm/1?000?h為單位。又因為每年(Y)平均計算有8?766小時(h),所以用戶又假?定x/1?000?h的不穩(wěn)定度等于8?8x/Y。
事實并非如此。長期不穩(wěn)定度(假定器件內部某個元件受損傷,其性能不是長期穩(wěn)定退變?)好?像是一種“醉漢走路”(drunkard’s?walk)行為,即器件在前1?000小時的?性能并不能代表后1?000小時的性能。這種長期不穩(wěn)定度是按經歷時間的平方根關系進行測?定的。這意味著,x/1?000?h的不穩(wěn)定度,其年漂移實際上應乘以8?766?,或者其年漂移大約乘以3,或每10年漂移大約乘以9。這項指標應該用μV/1?000?h來表示。
實際上,許多器件的長期穩(wěn)定度比上述情況好一點兒。如上所述,這種“醉漢走路?”方式假設器件的特性沒有改變。實際上,當器件老化后,器件制造應力趨于減小,從而使?性能變得更加穩(wěn)定(原始故障源除外)。既然很難定量地描述器件的這種長期穩(wěn)定度,不妨說?假定器件工作在低應力環(huán)境下,在使用壽命范圍內,其長期漂移速率趨于減小。這種漂移速?率的極限值?可能由1/f噪聲決定,可用時間比率自然對數平方根公式來計算,例如時間比率為8?8?x/Y?對應的漂?移速率為ln8?8=1?47,即一年漂移為1?47x。同理8?8年漂移為2?94x,7?7年漂移為4?4x,依次類推n年漂移為xln(8?8n)/ln8?8。?
讀者信箱
問:有一位讀者的來信由于直接引用篇幅太長,所以這里概括介?紹來信內容,他對本欄目(Analog?Dialogue?24?2,pp?20~21)中有關散粒噪聲或肖特基噪?聲(肖特基首次正確解釋了來自真空電子管中的散粒效應)提出了看法。該讀者特別反對將散?粒噪聲僅規(guī)定為一種結現象并且評論我們把運算放大器與其它半導體器件像兄弟關系一樣構?成的完整器件所帶?來的問題。他特別提出了散粒噪聲公式:
In=2qIB,單位?A
其中In為散粒噪聲電流有效值,I為流過某一結區(qū)域的電流,q為電子電荷,B為帶寬。該?公式似乎不包含依賴于特定結區(qū)域物理特性的任何物理量。因此他指出,散粒噪聲是一種普?遍現象,它與下述事實有關:任何電流都是一種電子流或空穴流,它攜帶離散電荷,從而由?上述公式計算出的噪聲恰恰表示了這種電流的粒子性。
他認為如果忽略承載電流的任何電路(包括純阻性電路)中的這種噪聲成分,都可導致嚴?重的設計問題。他計算通過任一理想電阻器的直流電流產生的噪聲來說明這種噪聲電流的?作用。如果對該電阻器僅施加52?mV電壓,那么產生的噪聲電流等于室溫下熱噪?聲電流;如果施加200?mV以上電壓,那么這種噪聲電流將成為主要電流噪聲源。
答:因為低噪聲運算放大器設計者已經不理睬這種主觀推測,那么他錯在哪里呢??上述推理的假設是上述散粒噪聲公式對導體有效。
實際上,散粒噪聲公式產生于載流子相互獨立的假設。盡管這種散粒噪聲確實是由穿過(?由結二級管或真空電子管構成的)勢壘的離散電荷形成的電流,但它并不是真正的?金屬導體。由于導體中的電流是由非常大量的載流子組成(單個載流子的流動非常慢),所以?與電流的流動有關的噪聲相應地也非常小,因此電路中的熱噪聲一般都忽略不計。
這里引用Horowiz和Hill在其論文中的一段話:“電流是離散電荷的流動,而不是像流?體一樣的連續(xù)流動。根據電荷量子的有限性產生了電流的統計波動性理論。如果這些電荷的?作用彼此獨立,那么波動電流為:
In(rms)=I?nR?=(2?qI?dc?B)?1/2?
其中q為電子電荷(1?60×10?-19?C),B為測量帶寬,rms表示有效值。例如1?A“穩(wěn)定?”?電流,波動電流的有效值為57?nA,測量帶寬為10?kHz。這說明波動程度大約為0?000006%?。這?種相對波動對小電流來講比較大。例如在10?kHz帶寬內,1?μA的“穩(wěn)定”電流,實際上電?流?噪聲有效值的波動為0?006%。即-85?dB。對于1?pA直流電流,同樣帶寬內其電流波動有效?值為?56?fA,即相對波動為5?6?%。可見,散粒噪聲豈不微乎其微碼?散粒噪聲,類似電阻熱噪聲?,屬于高斯噪聲和白噪聲。”
“早期給出的散粒噪聲公式假設電荷載流子具有獨立地形成電流的作用。這實際上是電?荷穿過勢壘的過程,例如結二極管電流,通過擴散電荷形成。與此相反,散粒噪聲在金?屬導體中的重要程度是不真實的,因為在金屬導體中,在電荷載流子之間存在著大范圍的相?關性。因此簡單阻性電路中的這種電流噪聲遠小于由散粒噪聲公式的計算值。在標準晶體管?電流源電路中我們提供了散粒噪聲公式以外的又一個重要公式,在這里負反饋起到減小散粒?噪聲的作用。”
 電子發(fā)燒友App
電子發(fā)燒友App










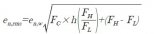















評論