實現鉑電阻溫度檢測器 (RTD) 的極高精度需要極其精確的信號調理和處理。本文介紹如何使用 ADuC706x 和幾個無源組件實現基于 MCU 的 RTD 傳感器接口。
鉑電阻溫度檢測器 (RTD) 是最精確的傳感器之一,可用于測量 –200°C 至 +850°C 范圍內的溫度。RTD 能夠實現 ±0.02°C 或更高的校準精度。然而,要獲得最大程度的準確度,需要精確的信號調理、模數轉換、線性化和校準。
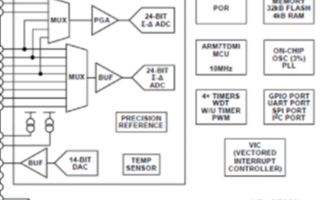
Analog Devices, Inc. MicroConverter? 產品系列包括在單芯片中具有 24 位 ADC 和 32 位 ARM7 MCU 的器件,信號調理電路非常適合 RTD 傳感器。
本應用筆記介紹了如何使用ADuC706x和幾個無源元件實現完整的 RTD 傳感器接口。本應用筆記基于 AN-709 應用筆記、使用 ADuC8xx MicroConverter 的 RTD 接口和線性化。
強烈建議使用本應用筆記中引用的軟件實用程序和示例代碼來實現基于 MicroConverter 的 RTD 傳感器接口。
硬件設計
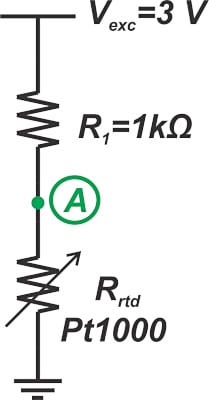
RTD 是一種傳感器,其電阻以精確定義的方式隨溫度變化。在嘗試了解 RTD 溫度電阻傳遞函數(非線性)的詳細信息之前,假設非線性是經過數字校正的。然后,專注于將 RTD 電阻轉換為數字值。一種常用的方法如圖 1 所示
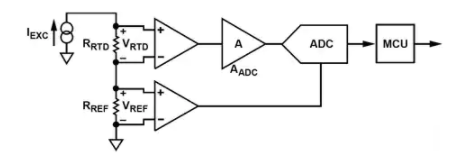
圖 1:RTD 接口硬件配置。
在圖 1 中,單個電流源 (I EXC ) 通過串聯方式激勵 RTD (R RTD ) 和精密參考電阻 (R REF ),產生 ADC 輸入電壓 (V RTD ) 和參考電壓 (V REF),分別。
ADC 的歸一化數字輸出(零輸入 = 0 和滿量程輸入 = 1)只是輸入電壓與參考電壓的比率乘以增益級 A ADC。
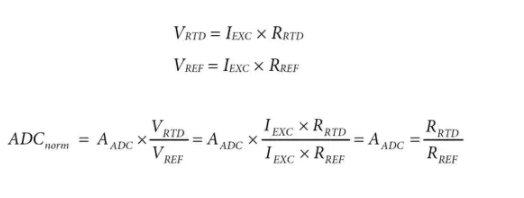
注意我是如何EXC抵消了上述等式。這意味著即使激勵電流發生變化或不精確,ADC 結果始終直接對應于 RTD 電阻與參考電阻的比率。選擇一個精密、低漂移的參考電阻意味著 RTD 電阻可以非常精確地知道,即使電流源的精度要低得多。
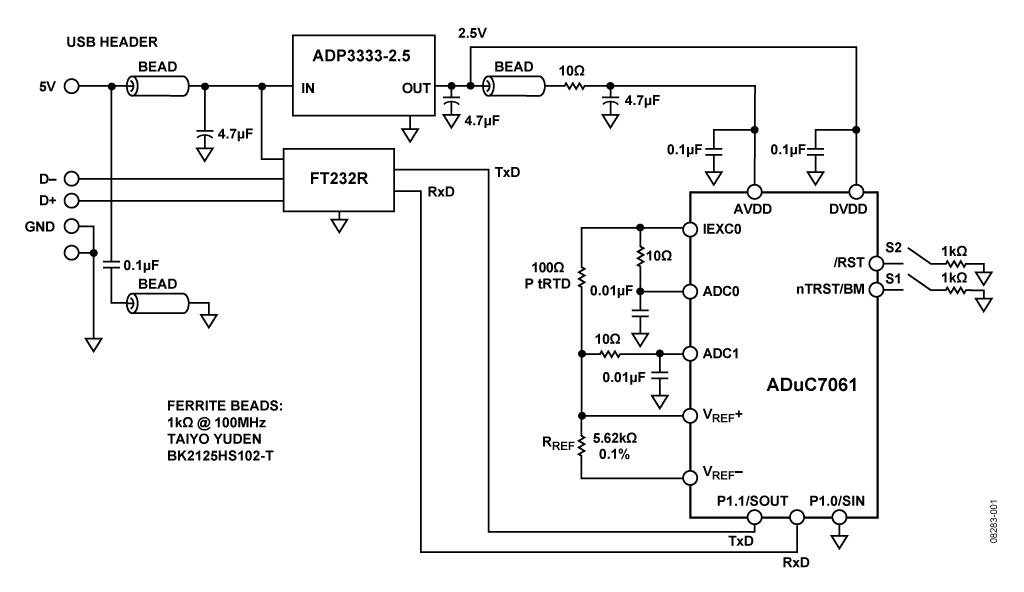
使用 MicroConverter 應用同樣的原理,圖 2 顯示了 ADuC706x 連接用于與 4 線 RTD 接口。請注意,這與圖 1 所示的總體拓撲相同,除了所有有源組件(勵磁電流源、V RTD和 V REF的差分輸入級、增益級 A ADC、ADC 本身和微控制器)都包含在 ADuC706x 芯片內部。二極管保護和 100Ω 電阻僅用于保護 ADuC706x 在端子塊出現過壓情況時免受損壞。
還包括其他外圍設備,例如用于數字通信路徑的串行通信端口。另請注意,添加了一些無源元件用于信號的 R/C 濾波和端子塊處的過壓保護。這代表了一個完整的實現,只需要一個電源和數字接口所需的任何特定外圍芯片,例如 RS-232 或 RS-485 線路驅動器/接收器。
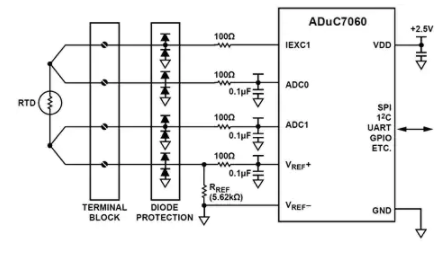
圖 2:使用 ADuC706x 的完整 RTD 接口電路。
根據 ADC 結果計算 RTD 電阻
如硬件設計部分所述,
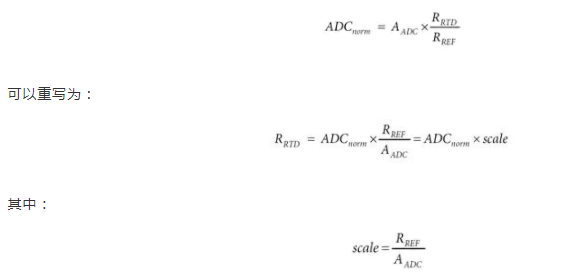
比例值是示例代碼中使用的固定比例因子。更進一步,可以將固定偏移值添加到等式中,從而得出
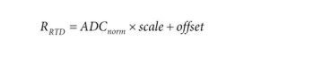
偏移項表示可用于補償誤差的固定偏移。這個偏移項將在校準部分進一步討論。在大多數情況下,該偏移項的值為零就足夠了。請注意,RTD 電阻的直接方程是作為 ADC 結果的函數,僅使用一對固定的比例和偏移值。
本應用筆記的其余部分考慮最常見的鉑 RTD 類型,其在 0°C 時的標稱電阻 (R 0 ) 為 100Ω。使用本應用筆記時,假設參考電阻值為 5.62 kΩ,它可以很好地匹配這種 RTD。有了這些組件值,并使用 ADuC706x,32 的內部增益是最高可用 ADC 增益設置,它仍然允許 RTD 覆蓋其完全指定的溫度范圍。
請記住,ADC范數被限制在 0 到 1 的范圍內,這定義了較高 ADC 增益下的溫度范圍限制。32 的增益對應于 0x8415 的 ADC0CON 值,或 37.5 mV 單極的范圍設置,其中:

為了對應這個增益設置,比例值計算為 175.625,其中:

這是示例代碼中使用的默認比例值。偏移項的默認值為零。這些等式假設 IEXC0 引腳上的激勵電流為 200 μA。這是通過設置 IEXCCON = 0x42 來配置的。
本節中 R RTD的公式只是通過軟件直接根據給定 ADC 轉換結果確定 RTD 電阻的方法。要將 RTD 溫度確定為其電阻的函數,需要了解 RTD 傳遞函數。
RTD 傳遞函數
鉑 RTD 傳遞函數由兩個不同的多項式方程描述:一個用于低于 0°C 的溫度,另一個用于高于 0°C 的溫度。

請注意,符號從 R RTD更改為 R RTD(t) 反映 RTD 電阻是其溫度的函數。圖 3 顯示了 RTD 傳遞函數(電阻繪制為溫度的函數)以及傳遞函數斜率在 0°C 時的線性擴展(用于視覺比較)。
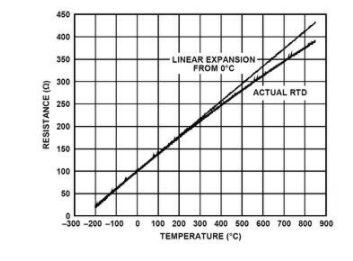
圖 3:RTD 傳遞函數。
前面的公式將 RTD 電阻定義為溫度 R RTD (t) 的函數。但是,要實現 RTD 傳感器接口電路,必須將 RTD 溫度確定為其電阻 T RTD (r) 的函數。考慮到 RTD 的非線性傳遞函數,這可能不太直接。以下部分探討了此任務的有用技術。
線性化技術
在給定 RTD 傳遞函數的情況下,有許多不同的方法可以將溫度確定為 RTD 電阻的函數。本應用筆記探討了三種在嵌入式設計中有用的技術。這些技術特別適合基于 MicroConverter 的設計。表 1 概述了每種方法的優缺點。此處顯示的執行時間代表 ADuC7060 在核心時鐘速度為 10.24 MHz 下運行此處引用的 C 子程序的經驗測量值。
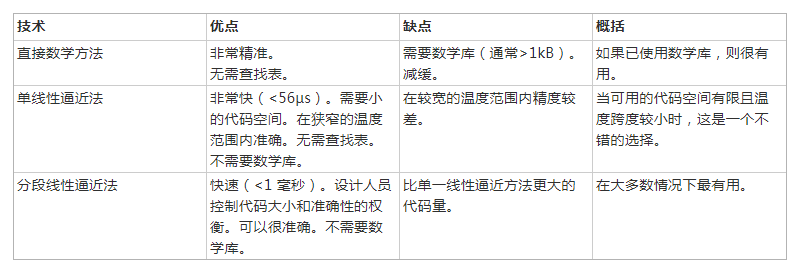
表 1:線性化方法的比較。
直接數學方法
在 RTD 傳遞函數部分,顯示了作為溫度函數 R RTD (t) 的 RTD 電阻的明確數學方程。是否可以將這些方程反過來并求解 RTD 溫度作為其電阻 T RTD (r) 的函數的表達式?對于定義正溫度行為的方程來說,這是一項相當簡單的任務,因為它只是一個二次方程。二次方程的解產生兩個表達式;要確定哪一個是正確的,只需替換幾個已知值。對于 0°C 或更高溫度下的 RTD 溫度,結果為以下公式:

這有利于實時計算,因為 Z 1到 Z 4是常數和絕對值,因此需要較少的計算。上述 T RTD等式(r) 被稱為正函數,因為它與 0°C 及以上的溫度有關。由于這是一個直接的數學解決方案,因此在該范圍內它是 100% 準確的。求解該等式時,在 ARM7 C 代碼中使用 32 位浮點數學運算的舍入誤差約為 +0.0001°C/–0.0005°C。這對于任何實際目的來說都足夠接近 100% 的準確度。當使用內核時鐘速度為 10.24 MHz 的 ADuC706x 運行 RTDmath.c 的示例 C 例程時,該等式的執行時間小于 750 μs。
前面的公式僅適用于 0°C 及以上的溫度。R RTD的方程定義負溫度行為的 (t) 是一個四階多項式(在擴展第三項之后),并且對于求解作為電阻函數的溫度的單一表達式是不切實際的。然而,利用計算機數學工具可以幫助找到逆傳遞函數的近似值。
使用 Mathematica? 或類似的軟件數學工具為 0°C 或更低溫度下的 RTD 溫度得出以下最佳擬合多項式表達式:
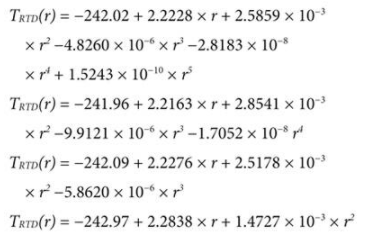
這四個方程被稱為負函數,因為每個方程僅適用于 0°C 及以下的溫度。頂部(五階)方程最準確,但計算時間最長,而底部(二階)方程精度最低,但計算速度最快。表 2 給出了這些負函數的一些特性,圖 4 顯示了每個函數的誤差隨溫度變化的曲線,以及(供視覺參考)正函數的誤差擴展到負溫度空間。
請注意,在圖 4 中,在接近零的負溫度下,正函數的誤差實際上比二階、三階或四階負函數的誤差要小。示例代碼 RTDmath.c 通過使用正函數來利用這種行為,即使在稍微負的溫度下也是如此。確定應使用正函數還是負函數的實際閾值因使用的負函數(二階、三階、四階或五階)而異,并在表 2 的閾值列中表示。這個閾值,正函數產生較低的誤差;低于此閾值,負函數會產生較低的錯誤。表 2 中的方程式精度列僅代表低于相應閾值的溫度的誤差。

1執行時間和方程精度是在 ADuC706x 上以 10.24 MHz 的核心時鐘速度運行 RTDmath.c 的示例 C 例程的經驗測量的。
表 2:最佳擬合多項式方程(負函數)的特征。
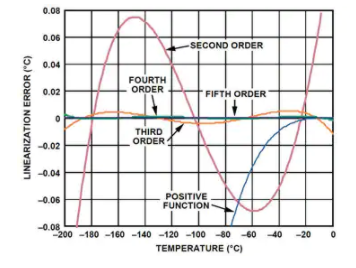
圖 4:最佳擬合多項式方程(負函數)的誤差圖。
用于線性化的直接數學技術的一個缺點是它需要浮點冪和平方根函數,例如 IAR Systems 的 IAR 編譯器的數學庫中的函數。僅這些浮點數學函數通常會增加超過 1kB 的代碼大小。使用分段線性逼近方法部分中描述的分段線性逼近方法,可以使用更小的整體代碼大小實現相似或更高的準確度。但是,如果程序中的其他操作需要數學庫函數,則直接數學技術可能是最佳解決方案,因為這些庫函數已經可用。
單線性逼近法
在圖 3 中,請注意,在較小的溫度范圍內,RTD 傳遞函數類似于一條直線。如果所需的測量溫度范圍僅跨越整個 RTD 測量頻帶的一部分,則可能根本不需要對 RTD 信號進行線性化。在這種情況下,在所需測量溫度范圍內對傳遞函數進行最佳擬合線性近似通常可以產生足夠的精度。例如,在 –40°C 至 +85°C 的工業溫度范圍內,最佳擬合線性近似值精確到 ±0.3°C。
一般來說,作為 RTD 電阻 (r) 函數的溫度線性方程具有以下形式:
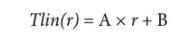
其中 A 和 B 是常數。
請注意,這些與 RTD 傳遞函數部分中描述的 A 和 B 不同。為 A 和 B 選擇最佳值以最小化誤差帶涉及一些此處未探討的數學。但是,本應用筆記附帶了一個非常簡單的軟件工具,它可以自動找到適合您特定溫度范圍的 A 和 B 的最佳值。本應用筆記中對該工具進行了檢查,但首先必須確定單個線性近似是否適合特定的設計要求。
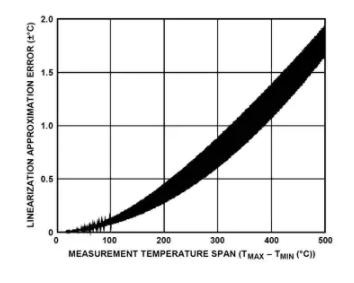
圖 5:單一線性近似誤差與測量溫度跨度的關系。
圖 5 顯示了在高達 500°C 的測量溫度范圍內產生的總近似誤差。對于超過 500°C 的跨度,近似誤差會隨著溫度跨度的增加而繼續降低。圖 5 曲線的不精確性(即數據跡線的寬度)是由于即使對于相同的溫度跨度,不同絕對溫度帶的誤差也是不同的。例如,–200°C 至 0°C 和 +600°C 至 +800°C 溫度范圍的精度不同,即使它們的精度都為 200°C。
圖 5 提供了一個粗略的誤差概念,以幫助衡量是否應將單一線性近似視為一種選擇。如果確定它可能是一個選項,則 RTD 系數生成器工具(在 RTD 系數生成器工具部分中描述)可以幫助確定特定溫度范圍的實際近似誤差,并且可以生成針對該溫度范圍優化的源代碼。
分段線性逼近法
將線性逼近更進一步,可以將任意數量的線性段概念化,以更好地逼近非線性 RTD 傳遞函數。生成這一系列線性段以使每個段的端點與相鄰段的端點相交,從而可以將其視為由直線連接的多個點。這些點(或系數)可以計算一次以最好地匹配 RTD 的非線性傳遞函數,然后永久存儲在 ROM 或閃存中。從這個系數表中,MCU 可以執行簡單的線性插值,以根據測得的 RTD 電阻確定溫度。
要了解這在實踐中是如何實現的,首先假設系數表已經存在。表中的每個系數只是傳遞函數上的一個點,由電阻和溫度表示。因此,該表采用以下形式:
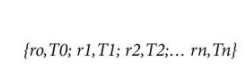
給定此表,MCU 的實時任務(確定給定電阻 r 下的溫度)首先確定哪兩個系數最接近所討論的點(稱為 {rm ,Tm} 和 {rn,Tn}),然后在這兩點之間進行線性插值以求解溫度。該范圍的實際線性插值公式(即,僅對 r m和 r n之間的 r 值有效)采用以下形式:
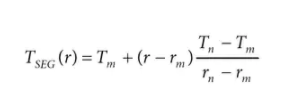
請注意,上述查找表中的每個系數都由兩個數字組成,一個代表電阻,一個代表溫度(本質上是傳遞函數中的 x 和 y 值)。因此,對于 N 個線性段(即 N + 1 個系數),總共必須將 2N + 2 個值存儲在內存中。為了減小查找表的大小,考慮一個由 N 個段組成的表,每個段跨越相等的電阻寬度。這樣的表只能存儲為一組溫度點,如下所示:
{T0; T1; T2; ... tN}
因為對于給定的系數 {r n ,T n },可以通過以下方式計算 rn 的值:
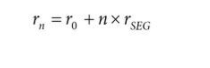
其中:
r 0和 r SEG是固定值,與系數表一起存儲在 ROM 中。
r 0是系數為零時的電阻{r 0 ,T 0 }。
r SEG是分隔相鄰系數的固定電阻跨度。
然后,給定段的線性插值公式變為
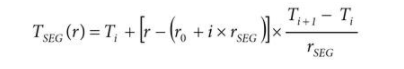
其中 i 表示正在使用哪個段(即,哪對系數),并使用 r 的值計算如下:

同樣,上述 T SEG (r)的表達式只不過是兩個系數 T i和 T i + 1之間的線性插值。為了在實踐中實現這一點,MCU 必須首先求解 i(根據最后一個方程),以便系數 T i和 Ti + 1是最接近 r 輸入值的兩個。然后,通過 i 求解,MCU 可以簡單地求解 T SEG (r) 方程以確定給定輸入電阻下的溫度。
這種分段線性逼近技術產生的總體誤差取決于段的數量(或系??數的數量,或查找表的大小)以及溫度的總體跨度。
圖 6 顯示了測量溫度范圍為 –200°C 至 +850°C 的線性近似誤差與查找表大小的函數關系(使用 RTD 系數生成器工具生成的優化系數)。請注意,如果減小測量溫度范圍,則在查找表相同大小的情況下會產生更好的誤差,或者在查找表較小的情況下會產生相同的誤差。
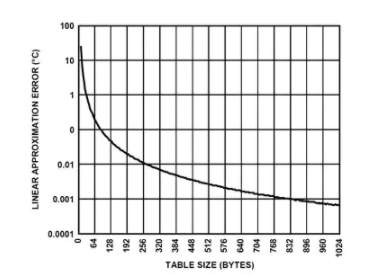
圖 6:分段線性逼近誤差與查找表大小的關系(-200°C 至 +850°C 范圍)。
RTD 系數生成器工具
實現分段線性化函數最困難的部分是生成查找表。但是,本應用筆記隨附的 RTD 系數生成器工具 (coefRTD.exe) 會自動為鉑金 RTD 執行此操作。這個簡單的 DOSexecutable 使用分段線性或單線性逼近方法協助基于 ARM7 的 RTD 接口設計。它執行以下任務:
- 為給定的溫度范圍和查找表大小生成優化的查找表系數。
- 指示產生的誤差帶和查找表大小。
- 在 ARM7 C 源代碼中生成完整的 RTD 線性化函數(包括查找表)。
- 根據給定的查找表生成一個誤差值表作為溫度的函數。
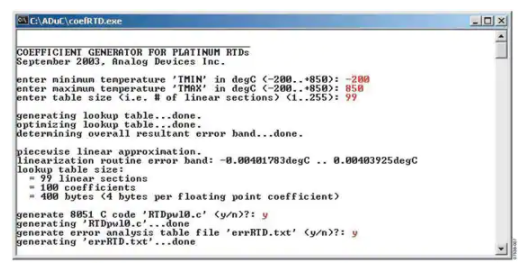
圖 7:具有分段線性近似的系數生成器會話示例(用戶輸入為紅色)。
圖 7 顯示了一個帶有用戶輸入的示例會話。請注意,該程序只要求用戶輸入三個參數(T MIN、T MAX和 N SEG)。該程序可以生成文件 RTDpwl0.c,它是一個完整的 C 源文件(一個定制的、用戶特定的查找表),可以按原樣包含在一個項目中,其中 T_rtd() 函數可以直接從函數中調用其他源文件。或者,可以將 RTDpwl0.c 的任何部分直接復制并粘貼到其他源文件中。
系數生成器還可以輸出錯誤分析文件 (errorRTD.txt),這是一個制表符分隔的文本文件,可以導入 Microsoft? Excel 或任何其他電子表格程序,以檢查線性逼近例程生成的錯誤。
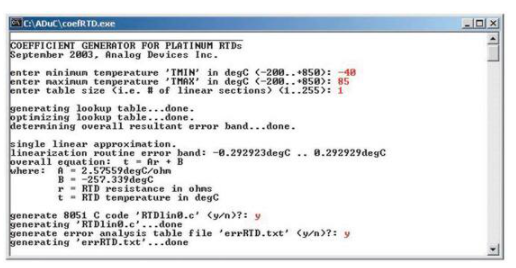
圖 8:具有單一線性近似的系數生成器會話示例(紅色為用戶輸入)。
系數生成器程序不僅為分段線性逼近生成線性化函數,還為單線性逼近生成線性化函數。為此,請為表格大小輸入 1 以僅指示單個線性段。
程序識別這一點并輸出與單線性逼近方法而不是分段線性逼近方法相關的結果,如圖 8 所示
ADuC706x 具有內置功能,用于校準 ADC 的端點誤差(偏移和增益誤差),如產品數據表中所述。但是,如果在校準過程中考慮到整個信號鏈,包括 RTD 本身,最終可能會得到較低的總體誤差,在這種情況下,內置 ADC 校準不會提供額外的好處。本應用筆記首先檢查整體校準,然后指出內置 ADC 校準可能仍然有用的一些情況。
到目前為止,假設 RTD 本身是完美的。然而,真正的 RTD 并不完美。就像現實世界中的其他任何東西一樣,它們也有與它們相關的錯誤,如 RTD 制造商的數據表所指定。幸運的是,這些錯誤中的許多都可以在軟件中輕松校準。本應用筆記中討論的校準功能可用作單點校準或兩點校準。該函數可以與任何線性化技術結合使用。
要了解單點校準原理上的工作原理,請參閱 RTD 傳遞函數部分中討論 R RTD (t) 的位置,并注意它主要由值 R 0定義,即 RTD 在 0 時的電阻攝氏度。對于最常見的 RTD,R0標稱 100Ω。但是,此 R 0值是 RTD 傳感器中最重要的誤差源,因為它可能因設備而異。此外,由于 R 0值簡單地乘以 R RTD (t) 表達式中傳遞函數的其余部分,因此由 R 0容差引起的誤差純粹是相乘的,因此可以通過調整R RTD作為歸一化 ADC 轉換結果的函數的以下表達式(如前所述) :

具體而言,如果可以將 RTD 帶到非常精確的已知溫度并執行 ADC 轉換,則校正后的比例值可以計算為:
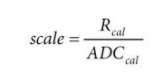
其中 ADC cal是模數轉換的實際歸一化結果,R cal是該 RTD 溫度下的理想(預期)電阻值。R cal可以使用 R RTD (t)的公式手動計算。通過這種方法(稱為單點校準),獲得校正的刻度值,補償 RTD R 0容差,同時也補償參考電阻的初始容差。為了更進一步,可以采用兩點校準,它不僅可以補償這些縮放誤差,還可以補償可能存在的任何偏移誤差。這樣做不僅需要調整比例值,還需要調整偏移值。
假設已經執行了單點校準,現在可以將 RTD 帶到第二個非常精確的已知溫度,并執行另一個 ADC 轉換。標度值的公式(即 R RTD與 ADC范數函數的斜率)為:
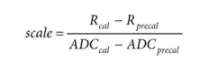
其中:
R precal和 ADC precal分別是前一個校準點的電阻和 ADC 轉換結果。
對于當前校準點, R precal和 ADC precal相同。
請注意,這是一種確定 R RTD與 ADC標準斜率的方法使用該線上的兩個點傳遞函數。只需注意偏移值,因為現在已知比例值,所以可以使用單個點來確定偏移值。偏移值的以下表達式通過求解上述 R RTD表達式的偏移,然后分別用 R precal和 ADC precal替換 R RTD和 ADC norm得出。 請注意,如果 R precal和 ADC precal

都為零(表示沒有先前的校準點),則刻度值的表達式與單點校準相同,偏移值的表達式為零,就像這是單點校準一樣。因此,相同的函數(示例代碼中的 Cal())可用于執行單點校準或兩點校準。
如果按原樣使用示例代碼,請按照以下步驟執行 2 點校準:
- 選擇兩個溫度進行校準,確保溫度點充分分開(理想情況下至少為總測量跨度的四分之一),以避免在測量溫度范圍的極端附近累積誤差。
- 將 RTD 帶到第一個溫度點,等待顯示結果穩定到新值,然后按終端(或終端仿真器)上的任意鍵以顯示用戶 I/O 菜單。
- 按照菜單提示校準到已知溫度,然后在出現提示時輸入溫度。
- 對第二個溫度點重復步驟 2 和步驟 3。
注意:對于單點校準,請跳過第 4 步。
雖然校準有很多好處,但也有許多系統考慮因素使其在某些應用中不切實際。如果無法按照步驟 1 至步驟 4 中的說明執行校準,請考慮執行系統 ??ADC 校準,如 ADuC706x 數據手冊中所述。為此,請將 RTD 更換為短路電阻 (0Ω) 并觸發系統零刻度校準。然后,用高精度 719.36Ω 電阻替換 RTD 并觸發滿量程校準。這補償了內部 ADC 誤差和 RREF 電阻的初始容差,但不考慮 RTD 本身的任何誤差。
請注意,ADuC706x(和所有其他 MicroConverter 產品)的另一個好處是它包含片上非易失性閃存,可用于存儲校準的比例和偏移值。這樣,芯片可以在每次系統上電時恢復校準值,而不是每次系統上電時都需要進行校準。
錯誤分析
數據采集??設計有許多誤差源,例如 ADC 線性度、輸入放大器噪聲、電阻器約翰遜噪聲、放大器溫度漂移和電阻器溫度漂移。確定給定設計中哪些占主導地位可能是一項艱巨的任務。幸運的是,ADuC706x 將所有有源級集成到一個完全由工廠指定的器件中,使誤差分析成為一項簡單得多的任務,但仍需要深入了解涉及非線性傳感器元件的設計。本應用筆記探討了迄今為止討論的特定硬件和軟件配置中最重要的幾個錯誤組件。
如果系統未針對特定 RTD 進行校準(使用單點或兩點校準),則 RTD 本身幾乎肯定是絕對誤差的最重要來源。該誤差應在 RTD 制造商的數據表中很好地量化,取決于所選 RTD 的具體型號。本應用筆記主要關注 RTD 本身以外的錯誤源。
噪音
要檢查的一種錯誤是噪聲。在此設計中需要考慮三個主要噪聲源:電阻約翰遜噪聲、放大器/ADC 輸入電壓噪聲和放大器/ADC 輸入電流噪聲。這些加在一起為平方和,因此當一個噪聲源甚至比另一個噪聲源稍大時,貢獻較小的源可以忽略不計。在這種特定情況下,主要噪聲源恰好是放大器/ADC 輸入電壓噪聲。具體而言,在討論的增益設置下,ADuC706x 輸入電壓噪聲規格為 0.25 μV rms,或約 1.65 μV pp。
將此輸入電壓噪聲轉換為產生的輸出溫度噪聲可能并不直觀,并且由于非線性電阻-溫度傳遞函數,會導致溫度噪聲隨 RTD 溫度而變化。結果如圖 9 所示。
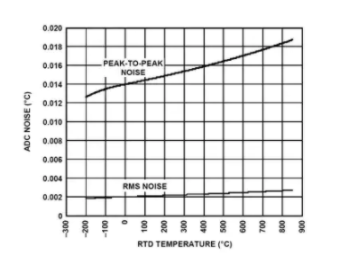
圖 9:ADC 噪聲與 RTD 溫度的關系。
請注意,即使在最高 RTD 溫度(即最差噪聲)下,峰峰值噪聲也始終低于 0.013°C;在較低的測量溫度下甚至更好。請記住,這種作為 RTD 溫度函數的噪聲變化不是 ADC 本身的函數,而是數字域中實現的非線性 T RTD (r) 傳遞函數的直接結果。
溫度漂移
另一個需要考慮的誤差來源是溫度漂移。具體來說,ADC 失調和增益溫漂以及參考電阻溫漂。這是直流誤差(失調和增益誤差)隨 ADC 芯片或參考電阻溫度變化的函數而變化。這與 RTD 調節電路的環境溫度有關,而不是與實際測量的 RTD 溫度有關。簡而言之,這兩個不同的溫度在此分別稱為環境溫度和 RTD 溫度。此外,由于非線性 T RTD (r) 傳遞函數,溫度漂移值(即對環境溫度的敏感性)隨 RTD 溫度的變化而變化。圖 10 所示的結果需要一些解釋。
圖 10 的 x 軸是 RTD 溫度。y 軸是溫度漂移(以°C 為單位),環境溫度每變化°C 時測量誤差的變化。例如,如果 RTD 溫度固定在 100°C,則 V REF漂移(使用 5 ppm/°C 參考電阻)約為 ±0.01°C/°C。因此,如果環境溫度變化例如 50°C,則測量溫度讀數的變化幅度可能高達 ±0.5°C(忽略溫度漂移的其他因素)。
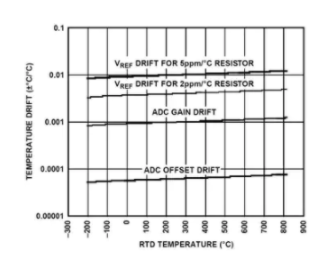
圖 10:溫度漂移與 RTD 溫度的關系。
很明顯,在環境溫度范圍通常跨越 -40°C 至 +85°C 或更高的工業環境中,溫度漂移可能是相當重要的誤差源。使用 ADuC706x 的片上溫度傳感器可以直接測量芯片溫度(密切跟蹤環境溫度),然后使用該測量的芯片/環境溫度來補償溫度漂移誤差。
這需要在制造過程中進行額外的溫度循環步驟,特別是使環境溫度達到兩個固定值,并在每個環境溫度下獲取零刻度和滿刻度 ADC 讀數。然而,軟件可用于在溫度傳感器精度和參考電阻器與 ADuC706x 之間的溫度梯度范圍內補償溫度漂移誤差。本應用筆記沒有進一步探討這種溫度漂移補償技術。但是,請注意,片上資源的存在使此選項成為可能,只需更改軟件即可。
RTD自加熱
RTD 自熱是另一個需要考慮的誤差來源。簡而言之,通過 RTD 施加電流會導致其耗散功率,從而提高 RTD 的溫度。幸運的是,由于 RTD 的激勵電流僅為 200 μA,因此對于 100 Ω R 0,RTD 消耗的總功率永遠不會超過 8 μW 。由這種小功率耗散引起的自熱量會有所不同,具體取決于所使用的 RTD 的具體型號,但通常可以忽略不計。
其他錯誤來源
其他錯誤來源大多可以忽略不計。直流端點誤差(偏移和增益誤差)可以使用校準部分中討論的校準技術進行完全校正。電阻約翰遜噪聲遠低于 ADC 的輸入電壓噪聲。唯一值得考慮的其他誤差源是 ADC INL(積分非線性或相對精度)。ADuC706x 數據手冊的典型 INL 規范為滿量程的 15 ppm,這導致輸出參考 INL 誤差約為圖 9 所示峰峰值輸出噪聲值的兩倍。
 電子發燒友App
電子發燒友App





















評論