1、相機內參數是與相機自身特性相關的參數,比如相機的焦距、像素大小等;
相機外參數是在世界坐標系中的參數,比如相機的位置、旋轉方向等。
相機標定(或攝像機標定):
一句話就是世界坐標到像素坐標的映射,當然這個世界坐標是我們人為去定義的,標定就是已知標定控制點的世界坐標和像素坐標我們去解算這個映射關系,一旦這個關系解算出來了我們就可以由點的像素坐標去反推它的世界坐標,當然有了這個世界坐標,我們就可以進行測量等其他后續操作了~上述標定又被稱作隱參數標定,因為它沒有單獨求出相機的內部參數,如相機焦慮,相機畸變系數等~一般來說如果你僅僅只是利用相機標定來進行一些比較簡單的視覺測量的話,那么就沒有必要單獨標定出相機的內部參數了~至于相機內部參數如何解算,相關論文講的很多~
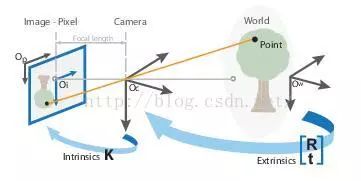
在圖像測量過程以及機器視覺應用中,為確定空間物體表面某點的三維幾何位置與其在圖像中對應點之間的相互關系,必須建立相機成像的幾何模型,這些幾何模型參數就是相機參數。在大多數條件下這些參數必須通過實驗與計算才能得到,這個求解參數的過程就稱之為相機標定(或攝像機標定)
相機標定的目的是確定相機的一些參數的值。通常,這些參數可以建立定標板確定的三維坐標系和相機圖像坐標系的映射關系,換句話說,你可以用這些參數把一個三維空間中的點映射到圖像空間,或者反過來。
相機需要標定的參數通常分為內參和外參兩部分。外參確定了相機在某個三維空間中的位置和朝向,至于內參,可以說是相機內部的參數(這好像是廢話...笑),我覺得需要引入一點光學的東西來更好地解釋一下。現有的相機都至少包含一個光學鏡頭和一個光電傳感器(CCD或CMOS)。
通過鏡頭,一個三維空間中的物體經常會被映射成一個倒立縮小的像(當然顯微鏡是放大的,不過常用的相機都是縮小的),被傳感器感知到。
理想情況下,鏡頭的光軸(就是通過鏡頭中心垂直于傳感器平面的直線)應該是穿過圖像的正中間的,但是,實際由于安裝精度的問題,總是存在誤差,這種誤差需要用內參來描述;
理想情況下,相機對x方向和y方向的尺寸的縮小比例是一樣的,但實際上,鏡頭如果不是完美的圓,傳感器上的像素如果不是完美的緊密排列的正方形,都可能會導致這兩個方向的縮小比例不一致。內參中包含兩個參數可以描述這兩個方向的縮放比例,不僅可以將用像素數量來衡量的長度轉換成三維空間中的用其它單位(比如米)來衡量的長度,也可以表示在x和y方向的尺度變換的不一致性;
理想情況下,鏡頭會將一個三維空間中的直線也映射成直線(即射影變換),但實際上,鏡頭無法這么完美,通過鏡頭映射之后,直線會變彎,所以需要相機的畸變參數來描述這種變形效果。
1).外參數矩陣。告訴你現實世界點(世界坐標)是怎樣經過旋轉和平移,然后落到另一個現實世界點(攝像機坐標)上。
2).內參數矩陣。告訴你上述那個點在1的基礎上,是如何繼續經過攝像機的鏡頭、并通過針孔成像和電子轉化而成為像素點的。
3).畸變矩陣。告訴你為什么上面那個像素點并沒有落在理論計算該落在的位置上,還tm產生了一定的偏移和變形!!!
2、攝像機內參、外參矩陣
在opencv的3D重建中(opencv中文網站中:照相機定標與三維場景重建),對攝像機的內參外參有講解:?
外參:攝像機的旋轉平移屬于外參,用于描述相機在靜態場景下相機的運動,或者在相機固定時,運動物體的剛性運動。因此,在圖像拼接或者三維重建中,就需要使用外參來求幾幅圖像之間的相對運動,從而將其注冊到同一個坐標系下面來?
內參:下面給出了內參矩陣,需要注意的是,真實的鏡頭還會有徑向和切向畸變,而這些畸變是屬于相機的內參的。?
攝像機內參矩陣:

其中,fx,fy為焦距,一般情況下,二者相等,x0、y0為主點坐標(相對于成像平面),s為坐標軸傾斜參數,理想情況下為0
攝像機外參矩陣:包括旋轉矩陣和平移矩陣?
旋轉矩陣和平移矩陣共同描述了如何把點從世界坐標系轉換到攝像機坐標系
旋轉矩陣:描述了世界坐標系的坐標軸相對于攝像機坐標軸的方向?
平移矩陣:描述了在攝像機坐標系下,空間原點的位置
例:
?33
d
?
? ? 7.3582167224957209e+002 ? ? ? ? ? ? ? ? ?0. ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 1.5950000000000000e+002
0.?? ? ? ? ? ? ? ? ? ? ?7.3582167224957209e+002 ? ? ?1.1950000000000000e+002
0. ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?0. ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?1.
二、 一些疑問
Q1:標定時棋盤格的大小如何設定,對最后結果有沒有影響?
A:當然有。在標定時,需要指定一個棋盤方格的長度,這個長度(一般以毫米為單位,如果需要更精確可以設為0.1毫米量級)與實際長度相同,標定得出的結果才能用于實際距離測量。一般如果尺寸設定準確的話,通過立體標定得出的Translation的向量的第一個分量Tx的絕對值就是左右攝像頭的中心距。一般可以用這個來驗證立體標定的準確度。比如我設定的棋盤格大小為270 (27mm)???,最終得出的Tx大小就是602.8 (60.28mm),相當精確。
Q2:通過立體標定得出的Tx符號為什么是負的?
A:這個其實我也不是很清楚。個人的解釋是,立體標定得出的T向量指向是從右攝像頭指向左攝像頭(也就是Tx為負),而在OpenCV坐標系中,坐標的原點是在左攝像頭的。因此,用作校準的時候,要把這個向量的三個分量符號都要換一下,最后求出的距離才會是正的。
但是這里還有一個問題,就是Learning OpenCV中Q的表達式,第四行第三列元素是-1/Tx,而在具體實踐中,求出來的實際值是1/Tx。這里我和maxwellsdemon討論下來的結果是,估計書上Q表達式里的這個負號就是為了抵消T向量的反方向所設的,但在實際寫OpenCV代碼的過程中,那位朋友卻沒有把這個負號加進去。(一家之言,求更詳細的解釋)
Q3:cvFindStereoCorrespondenceBM的輸出結果好像不是以像素點為單位的視差?
A:在OpenCV2.0中,BM函數得出的結果是以16位符號數的形式的存儲的,出于精度需要,所有的視差在輸出時都擴大了16倍(2^4)。其具體代碼表示如下:
dptr[y*dstep] = (short)(((ndisp - mind - 1 + mindisp)*256 + (d != 0 ? (p-n)*128/d : 0) + 15) >> 4);
可以看到,原始視差在左移8位(256)并且加上一個修正值之后又右移了4位,最終的結果就是左移4位
因此,在實際求距離時,cvReprojectTo3D出來的X/W,Y/W,Z/W都要乘以16 (也就是W除以16),才能得到正確的三維坐標信息
Q4:利用雙攝像頭進行測距的時候世界坐標的原點究竟在哪里??
A:世界坐標系的原點是左攝像頭凸透鏡的光心。
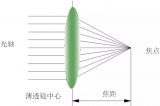
說起這個,就不得不提到針孔模型。如圖3所示,針孔模型是凸透鏡成像的一種簡化模型。當物距足夠遠時(遠大于兩倍焦距),凸透鏡成像可以看作是在焦距處的小孔成像。(ref: http://bak1.beareyes.com.cn/2/lib/200110/04/20011004006.htm)
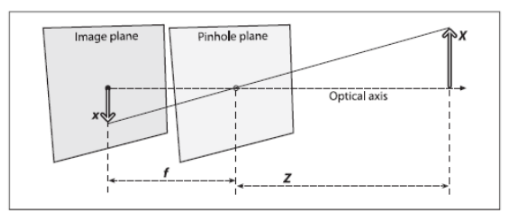
圖3. 針孔模型
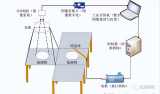
在實際計算過程中,為了計算方便,我們將像平面翻轉平移到針孔前,從而得到一種數學上更為簡單的等價形式(方便相似三角形的計算),如圖4所示。
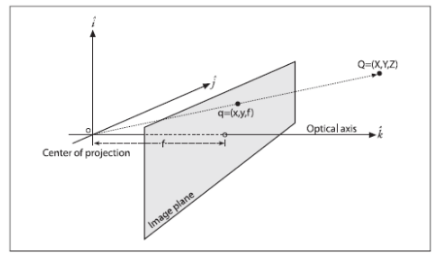
圖4. 針孔模型的數學等價形式
因此,對應圖2就可以知道,世界坐標系原點就是左攝像頭針孔模型的針孔,也就是左攝像頭凸透鏡的光心
Q5:f和d的單位是像素,那這個像素到底表示什么,它與毫米之間又是怎樣換算的?
A:這個問題也與針孔模型相關。在針孔模型中,光線穿過針孔(也就是凸透鏡中心)在焦距處上成像,因此,圖3的像平面就是攝像頭的CCD傳感器的表面。每個CCD傳感器都有一定的尺寸,也有一定的分辨率,這個就確定了毫米與像素點之間的轉換關系。舉個例子,CCD的尺寸是8mm X 6mm,分辨率是640X480,那么毫米與像素點之間的轉換關系就是80pixel/mm。
在實際運用中,我們在數學上將這個像平面等效到小孔前(圖4),這樣就相當于將在透鏡中心點之前假設了一塊虛擬的CCD傳感器。
Q6:為什么cvStereoRectify求出的Q矩陣cx, cy, f都與原來的不同?
A:這個在前文有提到過。在實際測量中,由于攝像頭擺放的關系,左右攝像頭的f, cx, cy都是不相同的。而為了使左右視圖達到完全平行對準的理想形式從而達到數學上運算的方便,立體 校準所做的工作事實上就是在左右像重合區域最大的情況下,讓兩個攝像頭光軸的前向平行,并且讓左右攝像頭的f, cx, cy相同。因此,Q矩陣中的值與兩個instrinsic矩陣的值不一樣就可以理解了。
編輯:黃飛
?
 電子發燒友App
電子發燒友App






























評論