本文中，將以MAX5891 作為測量和規格說明的特例。但所介紹的參數和測量方法可以用于其他的差分輸出、電流模式DAC。

線性參數說明

定義數據轉換器線性精度主要有兩個參數：積分(INL)和差分(DNL)非線性。INL是輸出傳輸函數和理想直線之間的偏差；DNL是轉換器輸出步長相對于理想步長的誤差。

可以采用兩種方法之一對INL進行定義：(1)端點INL或(2)最佳擬合INL。端點INL是采用DAC傳輸函數端點測得的實際值計算轉換器的線性度；最佳擬合INL則是計算傳輸函數的斜率獲得INL的峰值。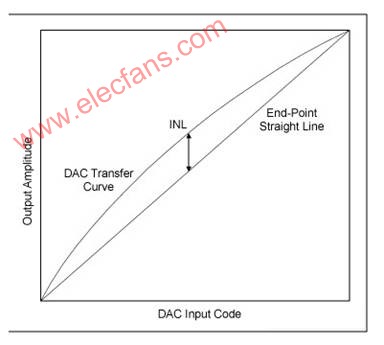



圖1a. 端點積分非線性誤差



圖1b. 最佳擬合積分非線性誤差

圖1a和圖1b以圖形的形式顯示了兩種測試方法與給定傳輸函數之間的關系。注意，兩種情況中，DAC傳輸函數曲線的數值和形狀都一樣。還要注意，圖1a的端點線性度有較大的正INL，而沒有負誤差。

采用圖1b所示的最佳擬合方法，將部分正誤差轉移到直線的負側，以降低報告的最大INL。注意，線性度誤差總量和直線計算結果相同。

DNL定義理解起來要難一些，確定最低有效位(LSB)的權值會影響DNL。DAC中需要考慮DNL沒有小于-1 LSB的編碼。小于這一電平的DNL誤差表明器件是非單調的。當輸出不隨輸入碼增大而減小時，或者輸出不隨輸入碼減小而增大時，DAC是單調的。圖2解釋了正、負DNL誤差，澄清了單調的概念。

測量線性度所采用的方法需要考慮待*估DAC的體系結構。優先選擇將電流模式DAC輸出轉換為電壓，因為這樣可以使用電壓表而不是電流表。普通的萬用表在測量電壓時分辨率要高于電流測量。電流源的配置決定了需要測量多少位編碼才能對器件性能進行精確的*估。



圖2. DNL誤差實例

有很多方法可以將電流(I)轉換為電壓(V)，主要取決于幾種因素。首先考慮使用萬用表進行測量，能夠得到的最高分辨率決定了精確測量的最小LSB權重。推薦LSB權重與儀表分辨率的比是100比1；儀表應能夠測量LSB的1/100。

待測DAC的輸出額定容限也影響了如何進行I至V的轉換。電流模式DAC輸出容限是指器件在輸出上能夠承受多大的電壓而不會對性能有影響。增大負載電阻會提高電壓擺幅和LSB的大小，但是容限限制了最大負載。

替代簡單的電阻轉換的方法是使用虛擬地配置的運算放大器，如圖3所示。由于DAC輸出電壓保持為零，這種配置的優勢是能夠提高LSB的大小，明顯高于容限限制。然而，放大器容限和線性度以及熱梯度會影響測量。同樣的，需要兩個匹配放大器來測量差分輸出器件。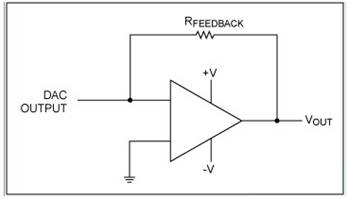



圖3. 虛擬地的I至V轉換

測量線性度時需要考慮的另一因素是待*估DAC的分辨率。器件分辨率越高，LSB越小。考慮MAX5891 (16位)、MAX5890 (14位)、MAX5889? (12位)器件。每一器件的滿量程輸出為20mA。使用50Ω負載時，相應的LSB大小為15.25?V、61.04?V和244.2?V。LSB越小，萬用表需要的精度和分辨率就越高。

考慮到DAC的分辨率，還應該確定需要多少位編碼才能精確地測量器件性能。16位器件有65,536個可能的輸入編碼，12位器件有4,096個。由于不可能人工測量所有這些編碼，因此，常用的方法是測量編碼子集。少量的編碼減少了采集數據所需要的時間，并且能夠提供非常精確的結果。掌握器件的體系結構有助于選擇某一器件的最佳編碼。

測量電流輸出器件的線性度時，溫度效應比較明顯。輸出負載電阻的功耗導致發熱，從而改變了電阻值(除非采用的電阻具有0ppm溫度系數)。解決這一問題的方法是轉換輸入編碼，有效地對負載功耗進行平均。

這里采用的方法非常適合自動測量，因為它能夠減小所有編碼的延遲時間。測量每一編碼及其補碼，例如0x4800，然后是0xB7FF。通過測量每一編碼及其補碼，負載平均功率保持固定，這是因為采用了從零到滿量程遞增的方式來測量最高有效位(MSB)輸入。由于在量程中部測量LSB，該方法不太適合，因為功率的變化相當小。

測量說明

以下是Maxim開發的幾種器件所采用的線性度測量方法。MAX5873 、MAX5875 、MAX5885、MAX5888 MAX5891、MAX5895 和MAX5898 /都采用了該方法進行測量。在最初設計*估和產品測試時進行了實驗室測量。雖然下面實例針對MAX5891，該方法也可以用于其他器件。

MAX5891采用了5-4-3-4分段結構。分段是指將一個16位器件有效地分成四個單獨的DAC，一個5位、一個4位、一個3位和第二個4位器件。5個MSB含有31個(25 - 1)等權重電流源，對于5位分辨率，每個輸入編碼采用一個等權重電流源。下一個4位使用15個源，再下一個3位使用7個。4個LSB是二進制權重電流源，每個低位比特等于前一比特值的一半。

電流源的總數57 (31 + 15 + 7 + 4)加上滿幅值和零值，確定了測量MAX5891線性度所需的最少編碼數。59次測量支持重新構建完整的DAC輸出傳輸函數。一旦確定了傳輸函數，即可計算線性度。該方法雖然縮短了測試時間，但降低了測量精度。表1列出了推薦的MAX5891編碼組。

表1. 5-4-3-4體系結構16位編碼組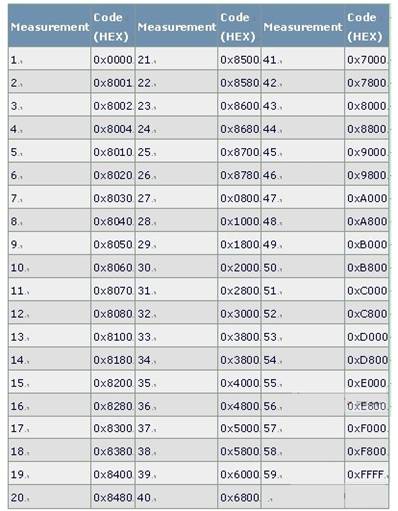



MAX5890和其他Maxim 14位器件使用5-4-3-2分段體系結構，14位體系結構的編碼組如表2所示。MAX5889和其他Maxim 12位器件使用5-4-3體系結構，12位體系結構的編碼組如表3所示。

表2. 5-4-3-2體系結構的14位編碼組



表3. 5-4-3體系結構的12位編碼組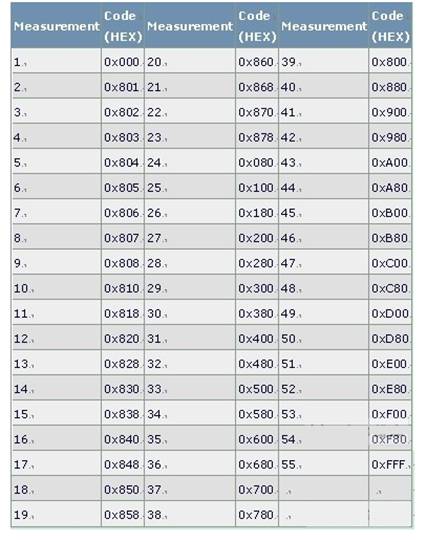



定義了編碼組后，必須解決采集測量點的問題。適合這類測量的萬用表是Agilent? 3458，分辨率高達8.5位。該表連接在MAX5891的OUTP和OUTN端之間，輸出端以50Ω負載接地。當DAC設置為20mA滿量程電流時，萬用表輸入得到的電壓擺幅是±1V。

萬用表量程設置為固定的1.2V，使用最大分辨率，得到10nV最小測量結果。切換表的量程會增大測量值的增益誤差；因此，使用單電壓量程可以避免其他的誤差源。由于需要鎖存數字輸入，MAX5891還需要時鐘信號。一旦連接好了萬用表、時鐘源、電源和數字輸入控制，就可以采集線性度測量點。

采集所有測量點后，需要畫出重建后的DAC輸出傳輸函數。由于對每一電流源都進行了測量，很容易產生對應于所有編碼的傳輸函數。例如，考慮器件的4個LSB。我們測量編碼0x8000、0x8001、0x8002、0x8004和0x8008。對于編碼0x8000，LSB計算的基準是DAC量程中部。LSB權重是在0x8001測得的電壓值減去在0x8000測得的電壓值。

在0x8001和0x8780之間測量的所有編碼采用相同的公式。0x0800到0xF800的其他點是MSB電流源，以編碼0x0000為基準進行計算。考慮編碼0x4F31作為各種電流相加的例子。

首先，我們需要確定哪一測量點什么時候相加能夠等于實例編碼。0x4800是小于目標編碼的最大MSB。從0x4F31中減去0x4800后的余數為0x0331。編碼0x0300是可以減掉的次最大編碼(0x8300 - 0x8000)，隨后是0x0030 (0x8030 - 0x8000)，最后是0x0001 (0x8001 - 0x8000)。

因此，可以采用下面的等式來表示編碼0x4F31的電壓值：

[V(0x4800) - V(0x0000)] + [V(0x8300) - V(0x8000)] + [V(0x8030) - V(0x8000)] + [V(0x8001) - V(0x8000)](公式1)

使用相似的等式，可以計算任意給定輸入編碼的電壓值。利用MATLAB?或Excel?軟件等工具可以很容易地計算所有編碼的電壓，重建全部的DAC傳輸。

一旦建立了傳輸函數，就可以計算線性度。第一步是根據傳輸函數的端點計算LSB的電壓值(端點法)。

VLSB = [V(0xFFFF) - V(0x0000)]/[2N - 1](公式2)

其中

N是器件分辨率 (16、14或者12位)

V(0x0000)是測得的DAC零標輸出電壓。

V(0xFFFF)是測得的DAC滿幅輸出電壓。

采用下面的等式來計算任意給定編碼的INL：

INLCODE(LSB) = [VCODE - (CODE × VLSB)]/VLSB(公式3)

其中

CODE是要計算的數字編碼。

VLSB是公式2中計算的電壓值。

VCODE是計算的DAC輸出電壓值。

下面的等式用于計算任意給定編碼的DNL：

DNLCODE(LSBs) = [VCODE - VCode-1 - VLSB]/VLSB(公式4)

其中

CODE是要計算的數字編碼。

VCODE是針對CODE計算的DAC輸出電壓值。

VCODE-1是針對CODE - 1計算的DAC輸出電壓值。

VLSB是公式2中計算的電壓值。

以下舉例說明利用MATLAB腳本計算MAX5889、MAX5890和MAX5891的線性度。每次計算都得到最小和最大DNL和INL誤差編碼和誤差值。實例還為所有編碼畫出了傳輸函數，得到INL和DNL。要求用戶輸入前面表格中所列出編碼的電壓測量值。必須按照所列順序輸入數值。

計算16位線性度的MATLAB腳本

function Lin16(Measurements)
%Calculate INL and DNL of a 16-bit device with a 5-4-3-4 segmentation architecture
% DacCodes is the range of possible input data to the 16-bit DAC
DacCodes=[0:65535]’;
%VOUT for each code is calculated from the measured points
%create a VOUT variable and fill it with zeros
VOUT=zeros(size(DacCodes));
%The first measurement is the zero-scale point, or code (0x0000)
ZS=Measurements(1);
VOUT(1)=ZS;
%The last measurement is the full-scale point, or code (0xFFFF)
FS=Measurements(length(Measurements));
VOUT(65536)=FS;
%Midscale is stored at position 43 of the input data array
MS=Measurements(43);
%The device has four segmentation levels
Segments=4;
%The decimal values for the LSB codes are 1, 2, 4 and 8
Seg1Codes=[1;2;4;8];
%The voltages for the LSBs are in positions 2-5 of the input array
for i=1:4
Seg1V(i)=Measurements(i+1)-MS;
end
%The second level of segmentation is controlled with input codes 16 through
%112 in steps of 16. Create the code array and fill the measurements for
%this segmentation level
Seg2Codes=[16:16:16*7]’;
for i=1:7
Seg2V(i)=Measurements(i+5)-MS;
end
%Segmentation level 3 uses input codes 128 through 1920 in steps of 128.
%Create the code array and fill the measurements array.
Seg3Codes=[128:128:128*(2^4-1)]’;
for i=1:15
Seg3V(i)=Measurements(i+12)-MS;
end
%Segmentation level 3 uses input codes 2048 through 63,488 in steps of 2048.
%Create the code array and fill the measurements array.
Seg4Codes=[2048:2048:2048*(2^5-1)]’;
for i=1:31
Seg4V(i)=Measurements(i+27)-ZS;
end
%The endpoints have been defined, now fill in the voltages for the
%remaining points of the DAC transfer function.
for i = 2:65535
targetcode=i-1;
VOUT(i)=ZS;
for s=31:-1:1
if Seg4Codes(s)<=targetcode
targetcode=targetcode-Seg4Codes(s);
VOUT(i)=VOUT(i)+Seg4V(s);
s=0;
end
end
for s=15:-1:1
if Seg3Codes(s)<=targetcode
targetcode=targetcode-Seg3Codes(s);
VOUT(i)=VOUT(i)+Seg3V(s);
s=0;
end
if targetcode==0
s=0;
end
end
for s=7:-1:1
if Seg2Codes(s)<=targetcode
targetcode=targetcode-Seg2Codes(s);
VOUT(i)=VOUT(i)+Seg2V(s);
s=0;
end
if targetcode==0
s=0;
end
end
if targetcode==0
s=0;
end
for s=4:-1:1
if Seg1Codes(s)<=targetcode
targetcode=targetcode-Seg1Codes(s);
VOUT(i)=VOUT(i)+Seg1V(s);
end
end
end
%Plot the transfer function
figure(1)
plot(DacCodes, VOUT);
xlabel(‘DAC Input Code’);
ylabel(‘Measured Voltage’);
axis([0 65536 -1.1 1.1]);
title(‘DAC Transfer Function’);
set(gca,’XTick’,0:16384:65536)
%Calculate the linearity
LSB=(max(VOUT)-min(VOUT))/65535;
INL(1)=0;
DNL(1)=0;
for i=2:65536
INL(i)=(VOUT(i)-(VOUT(1)+(i-1)*LSB))/LSB;
DNL(i)=(VOUT(i)-VOUT(i-1)-LSB)/LSB;
end
%Plot INL
figure(2)
plot(DacCodes, INL);
title(‘DAC Integral Linearity’);
xlabel(‘DAC Input Code’);
ylabel(‘INL (LSBs)’);
axis([0 65536 min(INL)*1.1 max(INL)*1.1]);
set(gca,’XTick’,0:16384:65536)
%Plot DNL
figure(3)
plot(DacCodes, DNL);
title(‘DAC Differential Linearity’);
xlabel(‘DAC Input Code’);
ylabel(‘DNL (LSBs)’);
axis([0 65536 min(DNL)*1.1 max(DNL)*1.1]);
set(gca,’XTick’,0:16384:65536)
txtstr=sprintf(‘INL MAX = %f’, max(INL));
disp (txtstr);
txtstr=sprintf(‘INL MIN = %f’, min(INL));
disp (txtstr);
txtstr=sprintf(‘DNL MAX = %f’, max(DNL));
disp (txtstr);
txtstr=sprintf(‘DNL MIN = %f’, min(DNL));
disp (txtstr);

16位腳本產生的曲線