MATLAB不但擅長於矩陣相關的數值運算,也適合用在各種科學目視表示(Scientific visualization)。
本節將介紹MATLAB基本xy平面及xyz空間的各項繪圖命令,包含一維曲線及二維曲面的繪制、列印及存檔。??
plot是繪制一維曲線的基本函數,但在使用此函數之前,我們需先定義曲線上每一點的x 及y座標。
下例可畫出一條正弦曲線:??
close all;
y=sin(x); % 對應的y座標??
plot(x,y);??
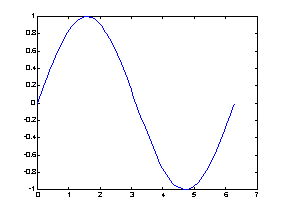 |
小整理:MATLAB基本繪圖函數
plot: x軸和y軸均為線性刻度(Linear scale)
loglog: x軸和y軸均為對數刻度(Logarithmic scale)
semilogx: x軸為對數刻度,y軸為線性刻度
semilogy: x軸為線性刻度,y軸為對數刻度??
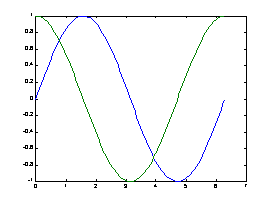
若要畫出多條曲線,只需將座標對依次放入plot函數即可:??
plot(x, sin(x), x, cos(x));??
?

?若要改變顏色,在座標對後面加上相關字串即可:??
plot(x, sin(x), 'c', x, cos(x), 'g');??
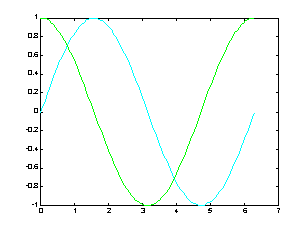 ??
???
若要同時改變顏色及圖線型態(Line style),也是在座標對後面加上相關字串即可:?
plot(x, sin(x), 'co', x, cos(x), 'g*');??
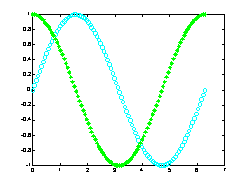 |
小整理:plot繪圖函數的叁數字元顏色字元圖線型態y 黃色. 點k 黑色o 圓w 白色x?xb 藍色+ +g 綠色* *r 紅色- 實線c 亮青色: 點線m 錳紫色-. 點虛線-- 虛線?
圖形完成後,我們可用axis([xmin,xmax,ymin,ymax])函數來調整圖軸的范圍:??
axis([0, 6, -1.2, 1.2]);?
 |
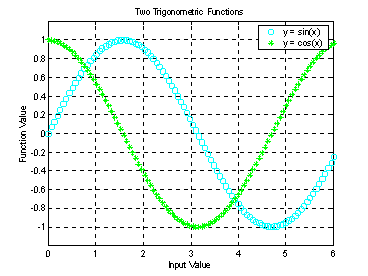
此外,MATLAB也可對圖形加上各種注解與處理:??
xlabel('Input Value'); % x軸注解??
ylabel('Function Value'); % y軸注解??
title('Two Trigonometric Functions'); % 圖形標題??
legend('y = sin(x)','y = cos(x)'); % 圖形注解??
grid on; % 顯示格線??
?
? 

我們可用subplot來同時畫出數個小圖形於同一個視窗之中:??
subplot(2,2,1); plot(x, sin(x));??
subplot(2,2,2); plot(x, cos(x));??
subplot(2,2,3); plot(x, sinh(x));??
subplot(2,2,4); plot(x, cosh(x));??
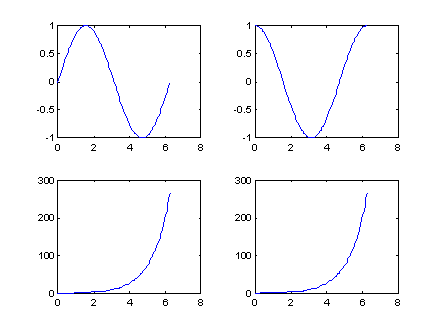 |
MATLAB還有其他各種二維繪圖函數,以適合不同的應用,詳見下表。??
小整理:其他各種二維繪圖函數
bar 長條圖
errorbar 圖形加上誤差范圍
fplot 較精確的函數圖形
polar 極座標圖
hist 累計圖
rose 極座標累計圖
stem 針狀圖
fill 實心圖
feather 羽毛圖
compass 羅盤圖
quiver 向量場圖?
以下我們針對每個函數舉例。?
當資料點數量不多時,長條圖是很適合的表示方式:??
close all; % 關閉所有的圖形視窗??
x=1:10;???
y=rand(size(x));???
bar(x,y);??
 |
?
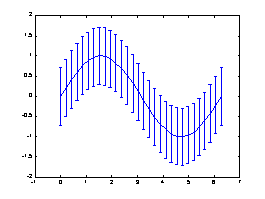
如果已知資料的誤差量,就可用errorbar來表示。下例以單位標準差來做資的誤差量:
x = linspace(0,2*pi,30);???
y = sin(x);??
e = std(y)*ones(size(x));??
errorbar(x,y,e)??
 |
?
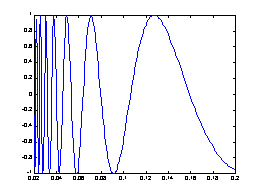
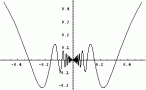
對於變化劇烈的函數,可用fplot來進行較精確的繪圖,會對劇烈變化處進行較密集的取樣,如下例:??
fplot('sin(1/x)', [0.02 0.2]); % [0.02 0.2]是繪圖范圍??
 ?
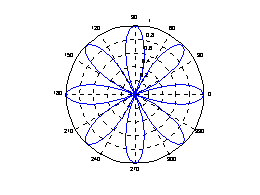
?若要產生極座標圖形,可用polar:??
theta=linspace(0, 2*pi);??
r=cos(4*theta);???
polar(theta, r);??
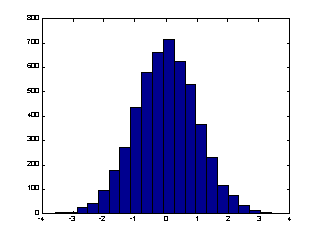
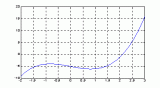
對於大量的資料,我們可用hist來顯示資料的分 情況和統計特性。下面幾個命令可用來驗證randn產生的高斯亂數分 :??
x=randn(5000, 1); % 產生5000個 m=0,s=1 的高斯亂數??
hist(x,20); % 20代表長條的個數??
 |
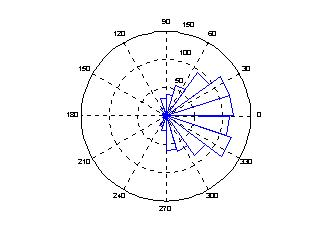
rose和hist很接近,只不過是將資料大小視為角度,資料個數視為距離,并用極座標繪制
表示:??
x=randn(1000, 1);??
rose(x);??
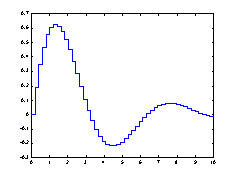
stairs可畫出階梯圖:??
x=linspace(0,10,50);??
y=sin(x).*exp(-x/3);??
stairs(x,y);??
 ?
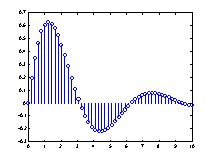
?stems可產生針狀圖,常被用來繪制數位訊號:??
x=linspace(0,10,50);??
y=sin(x).*exp(-x/3);??
stem(x,y);??
?
 |
?
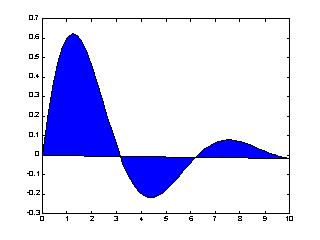
stairs將資料點視為多邊行頂點,并將此多邊行涂上顏色:??
x=linspace(0,10,50);???
y=sin(x).*exp(-x/3);??
fill(x,y,'b'); % 'b'為藍色??
 |
feather將每一個資料點視復數,并以箭號畫出:???
theta=linspace(0, 2*pi, 20);??
z = cos(theta)+i*sin(theta);??
feather(z);??
?
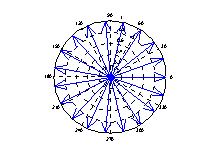
compass和feather很接近,只是每個箭號的起點都在圓點:??
theta=linspace(0, 2*pi, 20);??
z = cos(theta)+i*sin(theta);??
compass(z);??
 ?
? 電子發燒友App
電子發燒友App





















評論