原文作者:Suny Li
導語:隨著摩爾定律的臨近極限,如何在小小的芯片上集成更多的器件,成為新的挑戰。為此,集成電路設計的“新思路”成為解題關鍵。本文從芯片架構創新角度來闡釋電路設計新思路。
一? ?以3D的視角設計集成電路
在傳統大規模集成電路設計時,設計者把整個電子系統集成在一個芯片中,微處理器、模擬IP核、數字IP核,存儲器或片外存儲控制接口,都被集成在單一芯片上,形成一顆SoC上,并使用同一種工藝制造。 ? 由于芯片上的集成是基于2D集成技術,作為功能單元的晶體管均位于同一個平面上,即在晶圓平面上雕刻出納米級的晶體管。 ? 隨著系統復雜程度的提高,芯片的面積也會越來越大,這直接導致芯片良品率的下降。另外,隨著工藝節點逼近物理極限,摩爾定律也日漸式微,人們亟需找到新的方法來延續技術的發展,SiP與先進封裝技術、Chiplet與異構集成技術相繼出現,成為延續摩爾定律的良方妙藥。 ? 今天,我們再進一步,提出一個新思路,即以3D的視角設計集成電路。 ? 同樣以設計一顆SoC為例,我們不再把微處理器、模擬IP核、數字IP核,存儲器或片外存儲控制接口設計在同一個晶圓平面,而是把他們分別設計在不同的樓層(Storey),然后再將這些樓層組合起來,形成一個完整的芯片,如下圖所示。 ?
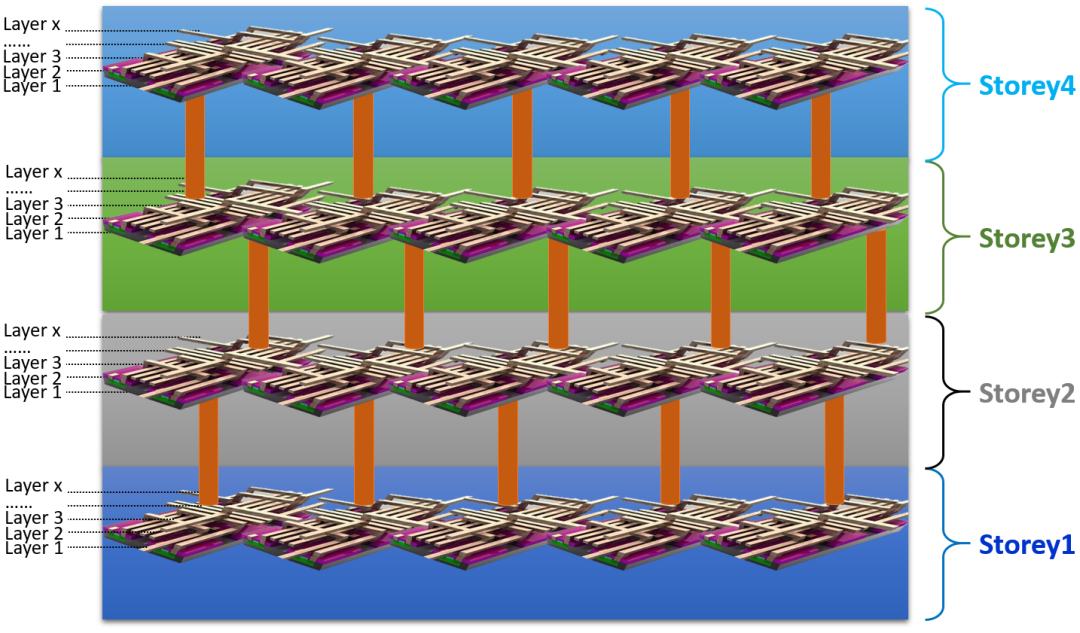
? 從圖中我們可以看出,每個Storey均有一層晶體管,并有多層布線將這些晶體管相互連接,不同的Storey之間采用TSV和RDL互連 (主要是TSV,RDL是在有些情況下,為了上下Storey金屬互連對齊時用到) 。 ? 對于不同的Storey (樓層) ,可以采用不同的工藝節點制造,同一個樓層上的晶體管,需要采用同樣的工藝節點制造。 ? 傳統設計集成電路的人可能會想,Storey之間的互連是先進封裝要干的事情。在本文中,情況發生了一些改變:從集成電路設計一開始,就要從三維的角度考慮進行設計了。 ? 因為集成電路設計離不開EDA工具,因此,“新思路”的難點其實在EDA工具這一塊,這也可以看成是集成電路設計和先進封裝設計的融合,而融合的起點在于EDA設計工具的融合。 ?
二? ?對EDA工具的新要求
傳統的IC版圖設計工具,先在硅基底上設計晶體管、電阻、電容等元器件,然后再通過多層布線將其連接,其信號互連和最終的布線都是在一個Storey上完成。 ? 在新的設計思路下,由于存在多個Storey,因此,除了考慮Storey之內的信號互連和布線,還需要考慮Storey之間的信號互連和布線。因此其網絡互聯和布線均是立體的,我們可稱之為立體網絡和立體布線。 ? 因為目前還沒有EDA工具能夠支持多個Storey這類的設計,因此無法找到確切的圖形來描述。下面兩張圖可暫且作為一個近似的描述:元器件位于空間的不同位置,其網絡的互連是立體的。 ?

? 同樣,當布線完成時,其布線也是立體的,除了Storey內部的元件需要布線連接,Storey之間也需要通過TSV和RDL連接。 ?

? 從上面的描述我們可以看出,EDA工具需要具備多版圖網絡優化的能力,即能夠在一個空間內,同時優化多個版圖之間的網絡連接,多個版圖以虛擬堆疊的形式位于空間的不同Storey。 ? 同時,IC版圖設計工具能同時處理多版圖設計,多個版圖可以位于同一個設計環境,也可以位于不同的設計環境,但多個版圖之間的數據交互需要統一進行協調和管理。 ? 目前,還沒有這樣的IC版圖設計工具,但已經有類似的工具在先進封裝設計中出現,具備近似的能力,例如HDAP高密度先進封裝設計工具XSI和XPD之間的協同設計。 ? 當然,除了設計工具,EDA仿真和驗證工具也同樣要跟上步伐。首先,對于設計工具構建的復雜數據模型,仿真和驗證工具要能夠正確解析。 ? 然后,仿真工具通過更強大的算法,進行仿真并得到正確的結果,驗證工具則需要保證從設計到生產數據的正確性和精準性。 ?
三? ?Cubic IC 設計方法學
上面描述的集成電路,有別于傳統的基于晶圓平面的集成電路,我們給其起了一個新的名稱:立方體集成電路 Cubic IC,可簡稱為CIC。 ? Cubic IC 由于其結構中包含了多個器件層,因此其設計方法和思路與傳統IC是完全不同的。 ? 在傳統IC的版圖設計中,我們需要將不同的功能模塊,按照2D的方式安排在版圖的不同區域,如下圖所示為海思麒麟980的版圖設計。 ?

? 按照 Cubic IC 的設計思路,我們可以將麒麟980的版圖設計沿著淺藍色的虛線分割成四部分,然后再將它們分別安排到不同的Storey,虛擬疊加起來,如下圖所示。 ?

? 每一個Storey內部的設計和傳統的IC設計相同,各個樓層Storey之間,通過TSV和RDL相連接,在設計的過程中,需要進行整體規劃和設計。 ? 這樣的話,芯片面積就減小為原有的1/4,并且由于采用了3D疊加方式,部分模塊之間的互連距離更短,從而性能也會得到提升。 ? 那么,最多可以疊加多少層呢?我們可以這么估算,Storey疊加的層數越多,芯片的面積就越小,一直到芯片堆疊的總厚度和芯片的長或寬的數值相當,即形成一個立方體,這也是立方體集成電路Cubic IC名稱的由來。 ? 我們以一個指尖大小的Cubic IC為例,假設其長和寬各為10mm,采用Cubic IC的設計思路,如果每個Storey減薄到50um,那么最多可以堆疊到200層,形成一個立方體集成電路。 ? 有人可能會問,形成立方體后,還可以堆疊更多嗎?理論上講是可以,但不建議,原因在后面講述。 ? 在Cubic IC的設計方法學中,整個芯片的最大厚度盡可能不超過芯片的長(寬),也就是,正立方體是其設計和制造的極限,其產品可以是一個扁平的立方體,而不建議是一個柱狀的立方體。 ?
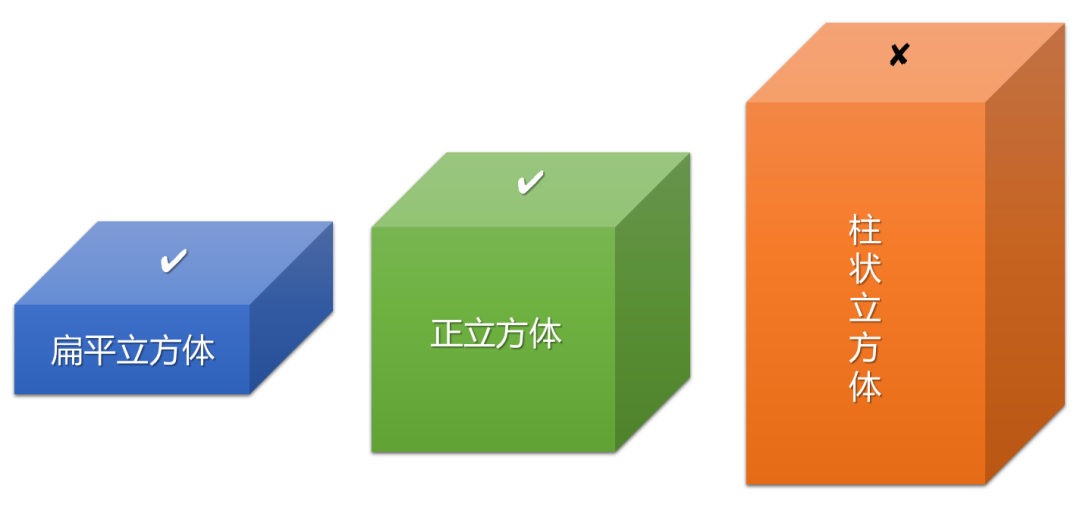
? 因此,我們在設計Cubic IC時,如果設置了芯片的長和寬,當芯片長和寬相等時,其厚度的最大值等于長(寬),如下圖A所示的范圍。 ? 并不是所有的Cubic IC都需要堆疊到一個正方體的形狀,可根據實際情況,設計其堆疊層數和厚度,例如下圖B所示的范圍。 ?
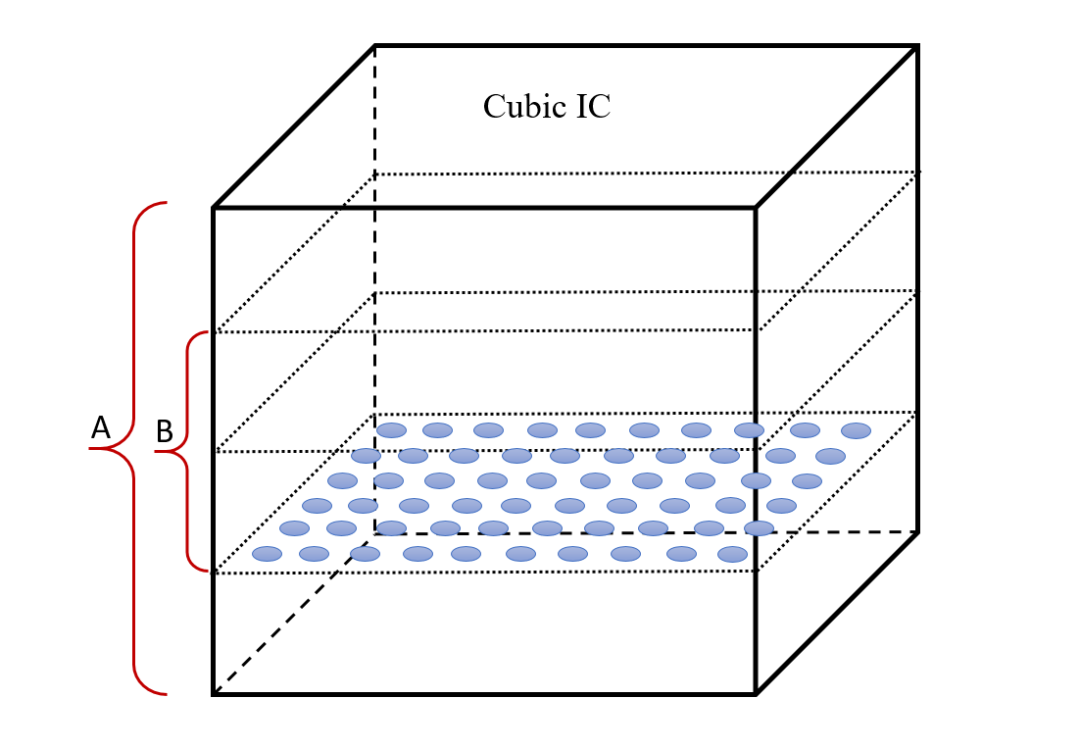
? 如果立方體的長和寬不相等,則厚度最大值取長寬二者的較小值。不過我建議最好保持長和寬相等,這樣芯片的材料利用率會更高。 ? 為什么正立方體被設計為 Cubic IC 設計和制造的極限呢?這就牽扯到信號傳輸距離的問題。我們知道,當信號在平面上傳輸時,信號在一個周期內可訪問到的區域是一個圓。 ?

? 隨著信號頻率的升高,圓的半徑會逐漸減小,圓的面積可能會小于芯片的面積,也就是說,即使在同一個芯片上,信號在一個時鐘周期內也未必能夠達到。 ? 這時候,曾經在PCB板級系統出現的內存墻現象在單個芯片上也會出現。 ? 如何能延緩甚至解決這個問題呢?就是向Z軸方向的空間發展。我們可以想象一個動態的過程,如果芯片內的晶體管總量保持不變,在向Z軸發展的過程中,XY軸是在不斷縮小的,一直到Z軸的和XY軸相等,形成一個正立方體。這時候信號在整個芯片中傳輸能耗最小,芯片性能也會最佳。 ? 當Z軸超越XY軸時,由正立方體逐漸變為柱狀立方體,芯片整體的能耗不再降低反而會升高,性能也會下降,和我們的設計初衷是違背的。這也解釋了上面我們不建議Cubic IC 發展為一個柱狀的立方體的原因。 ? 為了能夠精確地描述信號在一個周期內可在整個Cubic IC 三維空間內傳播的情況,我提出了一個李特思空間 LITS 的概念。 ?
四? ?關于李特思空間 LITS 的描述
? 李特思空間 LITS 是一個介于理想和現實之間的空間,嚴格來說是介于理想傳輸和現實傳輸之間的空間。 ? 李特思空間 LITS 全稱為:Li's Isochronous Transmission Space,李氏等時傳輸空間,簡稱為LITS,中文音譯為“李特思空間”,也寓意著進行了特別的思考而得出的空間。這次,我把Li姓加上了,是因為我目前自認為是第一個提出并運用這個空間的,當然如果有人能證明他提出并運用這個空間更早,我自然也會拱手相讓。 ? 在了解李特思空間 LITS 之前,我們先了解一下曼哈頓距離和等時傳輸區域。
? 4.1??曼 哈 頓 距 離?
? 曼哈頓距離是由赫爾曼·閔可夫斯基所創立,用以標明兩個點在標準坐標系上的絕對軸距的和。這位赫爾曼可不是別人,正是愛因斯坦的老師,那位創立了四維時空概念的閔可夫斯基。 ? 曼哈頓距離的正式意義為,在歐幾里德空間的固定直角坐標系上兩點所形成的線段對軸產生的投影的距離總和。 ? 在XY平面上,曼哈頓距離如下圖所示,即A點和B點之間的曼哈頓距離為,兩點之間的直線距離在X軸和Y軸投影之和。 ?
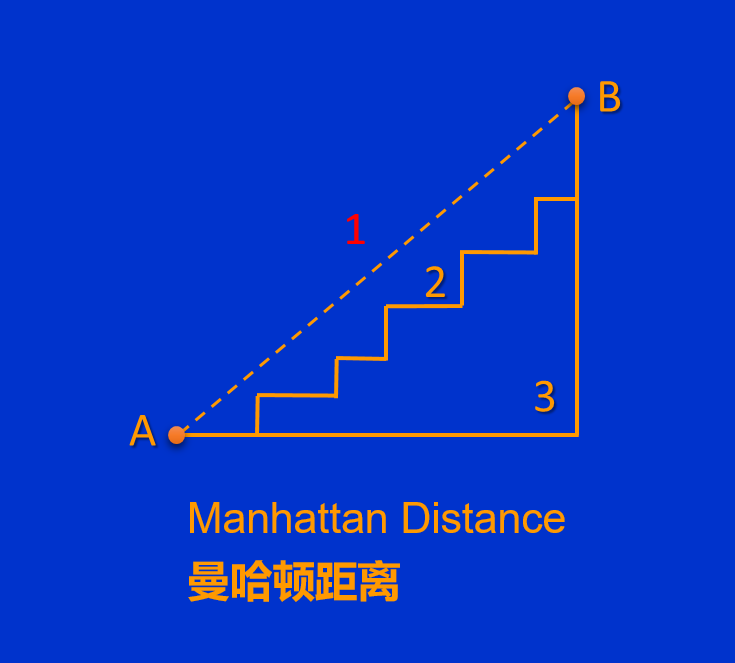
? 4.2??等 時 傳 輸?區 域?
? 在第三節中,我們講到,當信號在平面上傳輸時,信號在一個周期內可訪問到的區域是一個圓。而實際情況并非如此,問什么呢? ? 因為在實際的芯片的布線中,布線基本都是橫平豎直的,下圖所示為某存儲芯片的金屬布線1000倍顯微圖像,可以看出,所有的布線都是橫平豎直的。 ?

? 因此,我們可以得出,在芯片中從A點到B之間的物理布線距離,實際就是曼哈頓距離。那么,在相等時間內,信號在芯片上向不同方向傳播,可傳輸的距離范圍就不是一個圓,那會是什么樣的圖形呢? ? 下面,我們詳細分析一下。 ? 例如在一個時鐘周期內,信號在芯片平面上可傳輸的距離為 r,以 r 為半徑的圓是信號在理想情況下可傳輸的距離范圍。例如圓上的C點和B點。因為芯片上的實際布線遵循著曼哈頓距離布線的原因,同一個時鐘周期C點可以到達,而B點是不能到達的,只能到達中間的B’點,如下圖所示。實際的布線路徑也不會是1所代表的虛線,而可能是2代表的路徑。 ?
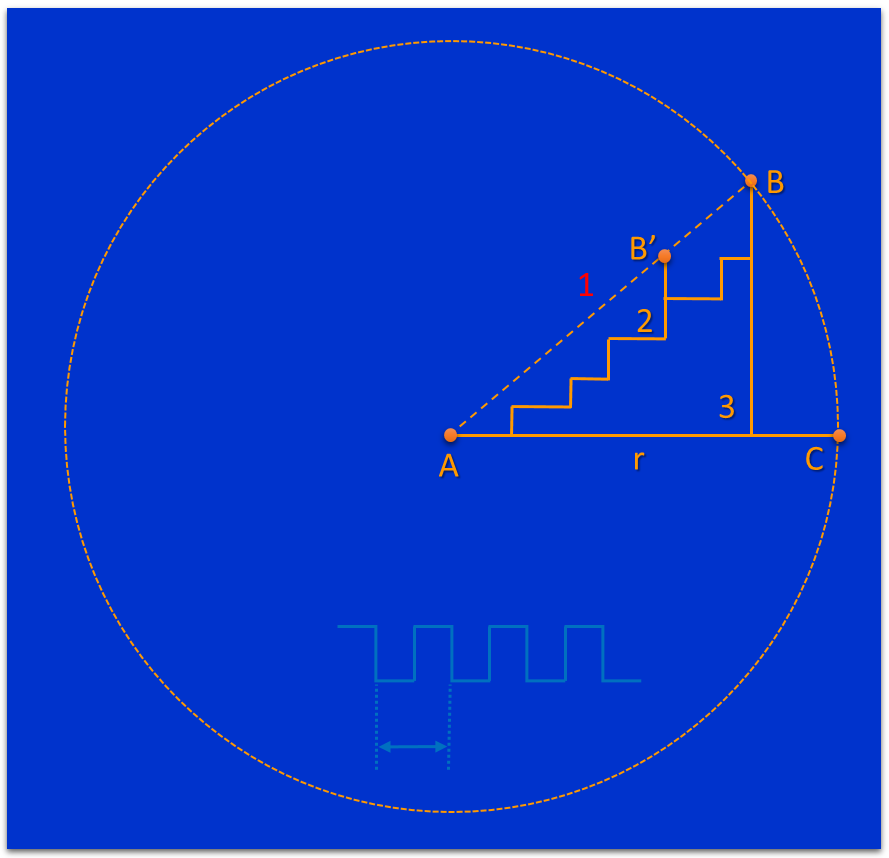
? 以A點為原點構建坐標系,根據曼哈頓距離的定義,C點和B’點都滿足其X坐標和Y坐標的投影之和相等,我們可得到等式:x + y = r,擴展到其它象限,我們可得出?|x|+|y|= r,四個象限的線段剛好組成了一個傾斜角為45度的正方形。 ?
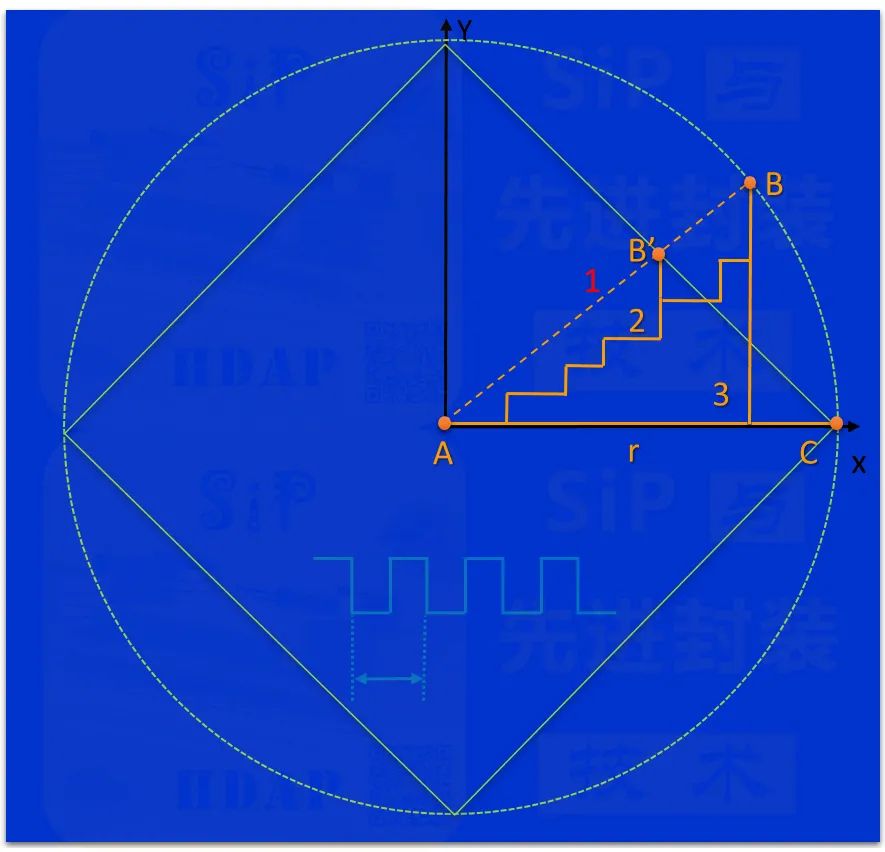
? 由此,我們可以得出,在芯片面積內,雖然在相等時間內(某一個時鐘周期),理想的傳輸距離范圍是一個圓,而實際的傳輸范圍是一個45度傾斜的正方形。 ?
? 有一些特殊情況,例如芯片上的布線不完全遵循曼哈頓距離布線,而是部分走了斜線,則傳輸的距離位于45度傾斜的正方形和其外接圓之間的區域。我們可稱之為等時傳輸區域 Isochronous Transmission Area,可簡稱為ITA。 ? 4.3??LITS?空 間?? ? 在本文中,我們描述的主要對象是立方體集成電路 Cubic IC,信號的傳輸距離范圍不僅僅在二維平面,而是在三維空間。那么,信號在三維空間傳輸,又會遵循什么樣的規律呢? ? 在理想情況下,信號在某一點向空間傳播,在相等時間內(某一個時鐘周期),理想的傳輸距離范圍是一個球,而實際的傳輸范圍是什么樣的呢? ? 在Cubic IC中,其布線的原則同樣遵循曼哈頓距離的原則,即沿著X軸Y軸Z軸的方向,因為曼哈頓距離通常應用于平面上的兩點,因此,在這篇文章中,空間兩點的曼哈頓距離我們稱之為空間曼哈頓距離。 ? 在Cubic IC中,從一點出發,以空間曼哈頓距離的方式進行布線,在相等時間內(例如某一個時鐘周期),實際的傳輸距離范圍可用方程??|x|+|y|+|z|= r 來描述,這是一個正八面體的表面方程。 ? 由此,我們可以得出,在 Cubic IC中,從某一點出發,在相等時間內,實際的傳輸距離是一個正八面體的表面。而理想的傳輸距離是一個球的表面。球和正八面體為內外相接的關系。 ? 李特思 (LITS) 空間定義:球體與其內接正八面體之間的空間,稱為李特思空間,其空間大小為: LITS = 4/3(π-1)r3 ? 該空間占整個 Cubic IC 立方體的空間比為: 4/3(π-1)r3÷?(8r3)=0.36 ? 這就是說,在一個虛擬的Cubic IC 立方體內,有36%的空間是從實際等時傳輸到理想等時傳輸之間的空間。 ? 這個空間的重要意義在于,在設計Cubic IC 時,可作為在3D空間布局IP單元時的依據或參考。 ? 下圖所示為LITS空間的圖形描述以及在Cubic IC 不同截面的空間大小。 ?
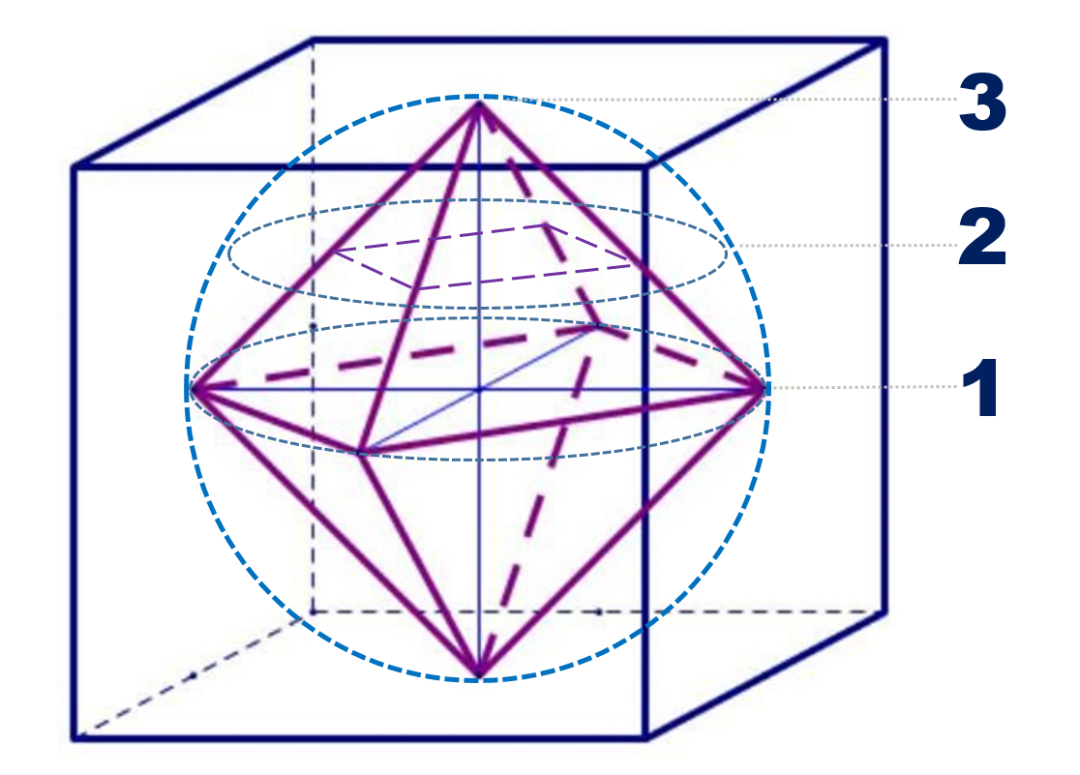
?
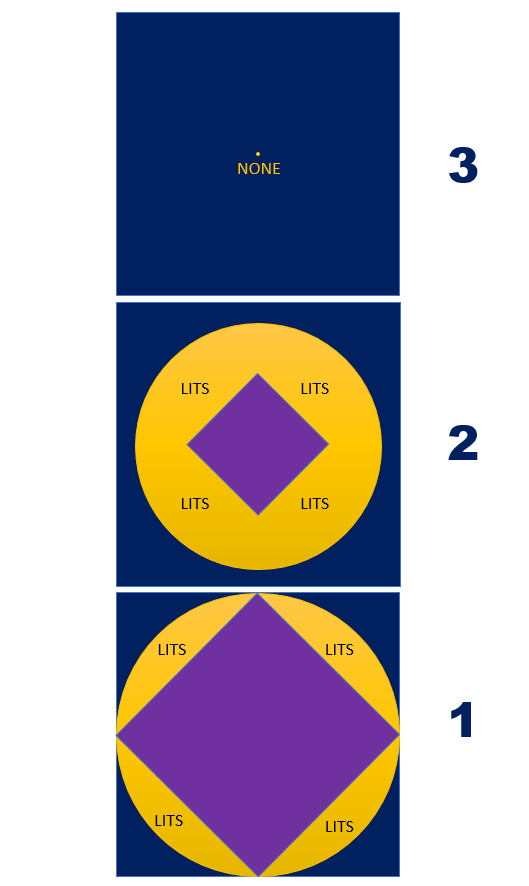
? LITS空間在不同截面的大小(金黃色區域) ? 我們知道,如果嚴格按照空間曼哈頓距離的方式進行布線,在相等的時間內,只能達到LITS空間的內表面,即正八面體的表面。如果在某些區域允許走斜線,則會進入LITS空間內部,但除了個別點,我們通常無法到達球體的表面,這就是現實和理想之間的距離。 ? LITS空間是一個虛擬的空間,可以作為設計Cubic IC時不同的IP模塊布局的參考依據,對于時序等長要求高的模塊,盡量安排在LITS空間內表面的附近,從而更容易實現物理上的等長。LITS空間在不同Z軸平面(Storey)上的投影,即可用于對IP模塊的位置進行劃分。 ? 在上面的描述中,我們是以Cubic IC 芯片中心作為參考點的情況,對于其它的關鍵點,也同樣需要構建虛擬的LITS空間,從而精確判斷信號傳輸所造成的延遲,精準地控制信息和指令的傳輸。 ?
五? ?關于有效功能體積的描述
? 在集成電路中,芯片的功能是由一個個晶體管組成的,我們稱之為功能細胞Function Cell,由多個功能細胞可以組成功能塊Function Block,由多個功能塊可以組成功能單元Function Unit。它們統稱為功能單位Function UNITs,有這些功能單位可組成微系統MicroSystem、常系統Common System、大系統Giant System。 ? 我們知道,無論是微系統、常系統、大系統,電子系統的體積中,功能單位所占的體積只占系統總體積的一部分,而其它的體積,并沒有功能,而是作為支撐、保護等因素而存在的。 ? 在本文中,我們將功能單位Function UNITs所占的體積稱為有效功能體積EFV (Effective Function Volume)。 ? 下面,我們以一顆芯片為例,來解讀一下有效功能體積。 ? 下圖是一個芯片的晶圓側剖面示意圖,從圖中我們可以看出,按照定義,有效功能體積包含了晶體管層和布線層,總厚度為約為5um,在布線層的上方是絕緣和保護層,包含聚酰亞胺Polyimide,氮氧化物Oxynitride,未參雜氧化物Undope Oxide,三者總厚度約為5um。 ?
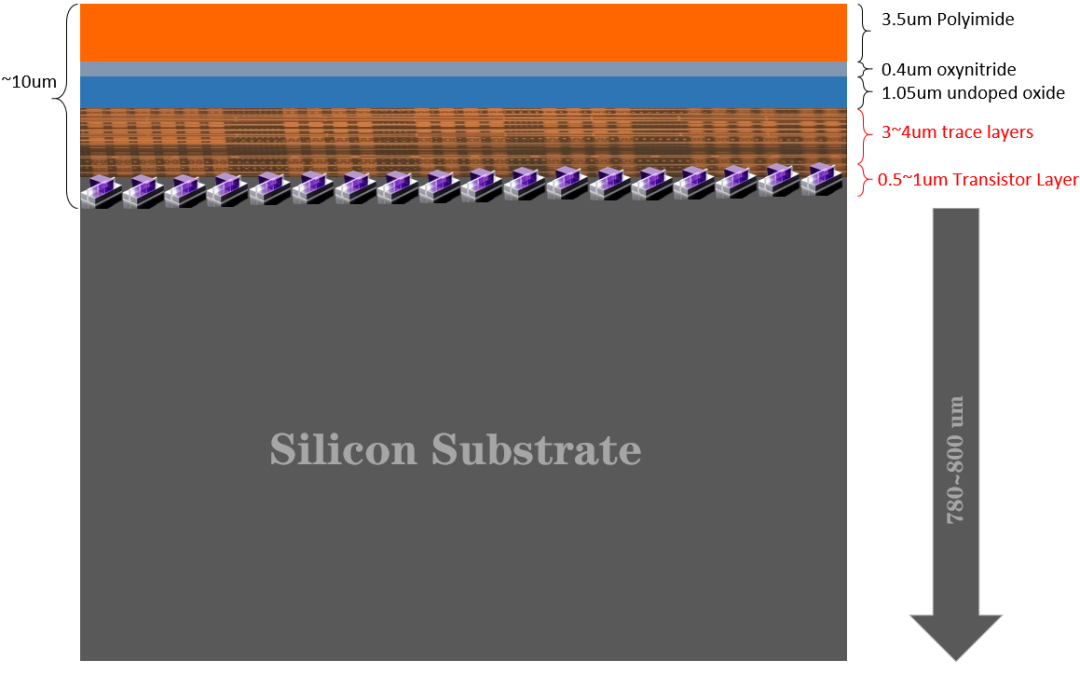
? 在晶體管層的下方是硅基底,其厚度大約為780~800um。通過計算我們可以得出,上圖中,有效功能體積所占的比例僅為芯片總體積的0.625%,還不到1%。 ? 那么,如何提升有效功能體積所占的比例呢?目前常用的方法就是進行晶元減薄。 ? 如果將晶圓減薄到100um,有效功能體積所占的比例為5%,如果將晶圓減薄到50um,有效功能體積所占的比例為10%,如果將晶圓減薄到20um,有效功能體積所占的比例為25%,就此打住吧,因為20um可能是目前減薄技術所能達到的極限了。 ? 通過晶圓減薄,我們使得有效功能體積占芯片總體積比例增加了40倍。如果依此去計算其功能密度,功能密度相當于增加了40倍。許多人正是從這一點上,認為通過先進封裝和異構集成技術,還是可以延續摩爾定律的。 ? 然而,事實上,這只是一種假象,不能因為功能密度的增加,就認為摩爾定律是可延續的。從摩爾定律提出的那一刻起,就注定了摩爾定律只是一個區間性的定律,最重要的原因就是摩爾定律曲線是指數增長的曲線,而以指數規律增長的曲線,在物理意義上都是不可持續的。 ? 有了有效功能體積的概念,在設計系統時,從最小的功能細胞Function Cell到最大的大系統Giant System,都應該逐級剖析其有效功能體積,并最大可能地提高有效功能體積所占的比例。 ?
六? ?Cubic IC 和 3D Chiplet 的區別
Cubic IC看起來和3D Chiplet有些相似,都是將大芯片分割后進行3D堆疊并通過TSV和RDL電氣互連。然而,它們有幾大不同之處。 ? 為了方便起見,我們后續可以將 Cubic IC 簡稱為 CIC。 ? 1)CIC 是以3D的View Point去設計集成電路,而3D Chiplet則并非從設計一開始就從3D的View Point去考慮整個集成電路的設計,通常是先考慮各Chiplet接口之間的匹配,并在制造的時候將小芯片進行堆疊并互連。 ? 2)CIC 不同的樓層(Storey)尺寸是完全相同的,堆疊后形成立方體形狀,3D Chiplet可以由不同尺寸的Chiplet組成。 ? 3)CIC 是對未來集成電路設計和制造的預期,3D Chiplet是目前先進封裝和異構集成可以實現的技術。 ? 4)Chiplet是IP芯片化的設計思路,將不同的IP分割成小芯片后在封裝級別進行集成,CIC并不需要將不同的IP分割,而是將這些IP合理地分配到不同Storey的不同區域。 ? 5)CIC 的樓層(Storey)數量可以堆疊到幾百層,3D Chiplet目前堆疊的層數是個位數。 ? 6)CIC 對EDA工具的要求很高,目前還沒有任何一家EDA工具可以支持,需要后續EDA廠商的積極研發,3D Chiplet對EDA工具的要求相對不高,目前的HDAP先進封裝設計工具例如XSI+XPD就可以很好支持了。 ? 7)CIC 的功能密度要遠高于3D Chiplet,因此其實現的難度和挑戰都要遠遠高于3D Chiplet。 ? 對此,我們可以這么理解,CIC是3D Chiplet甚至整個IC集成電路發展的終極目標,而3D Chiplet則是CIC發展的初級階段。 ?
七? ?關于 Cubic IC?制造方法的預期
我們知道,雖然芯片制造非常復雜,可細分為幾千道工藝,但總的來說,可分為三種類型:加工藝、減工藝和輔助工藝。 ? 加工藝也可稱為增材制造,即通過不斷地增加不同的材料,而完成最終的產品。 ? 3D打印就是一種典型的增材制造。在芯片制造中,濺射、離子注入就屬于加工藝。減工藝也可稱為減材制造,芯片制造中,最典型的減工藝就是刻蝕。至于光刻,雖然極其重要,其實是屬于輔助工藝,因為光刻就是輔助將圖形印刷在了晶圓上,并不會使晶圓上的材料增加或者減少。 ? 對于CIC的制造方法,我看可以參考下面一張圖,每一個樓層Storey生成相應的掩膜,和傳統的IC制造方法一樣,進行光刻、刻蝕、氣相沉積、離子注入、研磨、清洗等操作,然后將每個Storey的晶圓進行減薄Thining,通過混合鍵合Hybrid Bonding的方式將晶圓鍵合到一起,最后進行切割,得到CIC。 ?
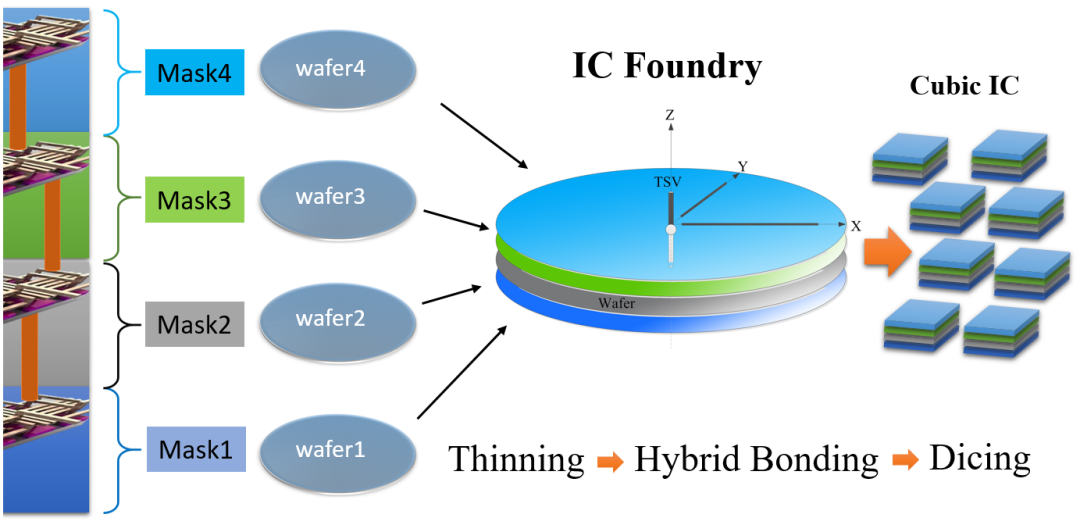
? 八? ?Cubic IC 帶來的挑戰
首先,所有的創新都會帶來新的挑戰,因此Cubic IC必然帶來新的挑戰! ?
8.1??設 計?的 挑 戰??
? 設計的挑戰主要來自兩點,1)對EDA工具的挑戰,2)對設計人員的挑戰。 ? 首先,我們來分析一下 CIC 帶來的EDA工具的挑戰,從傳統的IC設計轉為CIC設計,設計的復雜度會急劇提高。我們現在主流的集成電路,其晶體管上方的布線層可能多達十幾層,如果以CIC的方式進行設計,其Storey可能有數百層,這樣,組合起來,一個CIC,將會有數百層晶體管,其布線層更是多達數千層。現在看來,這對EDA工具的挑戰是極大的。 ? 同時,為了增加工藝靈活性,CIC允許不同的Storey(樓層)采用不同的工藝節點制造,例如Storey1采用7nm工藝,Storey2采用5nm,Storey3采用14nm,Storey4采用28nm工藝...... 需要在一個項目中管理多種工藝節點數據,也給EDA工具帶來了挑戰。 ? 下面,我們分析一下CIC給設計人員帶來的挑戰。 ?
從上面第七節的描述我們得知,在7nm工藝下,指尖大小的1立方厘米尺寸的CIC,其集成的晶體管數量大約在2.5萬億~5萬億,隨著工藝節點的縮小,加上CIC體積的增大,兩種因素疊加起來,其晶體管數量可能超越100萬億,是現在主流芯片的一萬倍,海量的數據如何處理,是帶給設計人員和設備的重大挑戰。 ? 電磁干擾的問題,在1立方厘米中集成了2.5萬億~5萬億的晶體管,在功能密度極大化的同時,會不會帶來電磁干擾的問題,也是設計人員需要重點考慮的。 ? 不過也不用過于擔心電磁干擾問題是由于堆疊層數太多而引起的,以現在成熟的7nm工藝,芯片間的互連布線間距最小在20~40nm左右,而以目前最先進的減薄工藝,可將晶圓減薄到20~40um,通過混合鍵合后,上下層晶體管的距離約為20~40um,可以看出,同一個Storey布線的間距和不同Storey的間距之間還有三個數量級(1000倍)的差別。因此,即使存在電磁干擾問題,也會先在同一個Storey出現,而解決方法和現在成熟的集成電路相仿即可。 ?
8.2??制 造?的 挑 戰??
? CIC是集成電路設計的新思路,必然包含新工藝和新方法,因此,能否制造出來是最為關鍵的環節。 ? 首先是每一個Storey的制造,這和傳統的IC制造方法并沒有特別大的區別,最主要的區別是在每個晶圓上事先要將進行Storey之間互連的TSV制作出來。并且要保證不同的Storey之間互連的對準,如果由于結構原因,上下層Storey的TSV無法對準,則需要通過RDL來進行輔助對準。 ? 然后,就是Storey之間的鍵合,現在有了混合鍵合工藝Hybrid Bonding,互連間距可以縮小到10um,相當于在1平方毫米可以多達10000個互連,在未來,Hybrid Bonding可支持每平方毫米100萬個互連,這樣的互連密度,是可以滿足CIC的需求的。
? 8.3??散 熱?的 挑 戰?
? ? 以CIC的思路去設計集成電路,必然會形成空間功能密度的極大化,而晶體管數量的劇增必然帶來熱量的增加,如何把這些熱量散發出去呢? ? 首先,要相信,這個問題是可以解決的! ? 先回顧一下芯片耗能和散熱的歷史。在2001年的國際固態電子電路會議上,專家們曾經指出,如果芯片耗能和散熱的問題得不到解決,到2005年芯片上集成了2億個晶體管時,就會熱得像“核反應堆”(1000℃),到2010年時就會達到火箭發射時噴嘴的高溫水平(3000℃),而到2015年就會與太陽的表面一樣熱(6000℃)。 ?
20年過去了,我們手機中的處理芯片晶體管數量已經達到了百億級別,芯片的溫度既沒有像太陽表面一樣熱,也沒有達到火箭噴嘴的水平,更不用擔心手里的握著“核反應堆”。目前我們手機里的主要芯片晶體管數量都在100億量級,是專家們曾經預測的50倍,依然可以穩定地工作,手機拿在手中,大多數時間我們甚至都很難感受到芯片發出的熱量。可見芯片工程師的智慧還是可以相信的。 ? 具體如何解決芯片耗能和散熱的問題,主要從兩大方面考慮,1)降低芯片功耗,2)降低散熱通道的熱阻。降低芯片功耗可以從動態功耗、靜態功耗、傳輸功耗三個方面入手;降低散熱通道的熱阻可以從新傳熱材料、新散熱結構兩方面考慮。 ?
總 結
這篇文章中提到的幾個重要概念:如立方體集成電路CIC,等時傳輸區域ITA,李特思空間LITS,有效功能體積EFV。 ? ? CIC的設計與制造,是一個非常難以實現的目標,實現需要努力。
編輯:黃飛
?
 電子發燒友App
電子發燒友App






















評論