Solidity作為一個程序語言，寫出來的Smart Contract就跟所有程序一樣，有時候會有Bug。然而Smart Contract上的Bug很可能比一般程序中的Bug還要嚴重，因為一旦放到鏈上就再也無法被修改了，最知名的莫過于DAO attack。于是有人將腦筋動到另一個依然還未被廣泛應用的領域上— —正規驗證（Formal Verificatinon，也有人稱為形式化驗證）。

本篇文章介紹的內容則是正規驗證前必須的工作，即定義一個語言的語意（semantics）。在一個語言中，一個語句的語義指的是這段指令所代表的「意思」。看到這大家可能會有個疑惑，為什么一個指令的意思需要另外定義？不是全部都寫在規格書跟編譯器里了嗎？原因是，就算是寫在規格中的語法，其真正的意思也時常是沒被精確定義的，如果僅是寫在規格書中，那一個指令結束后，整個電腦的狀態（在EVM可以指整個Ethereum的Global State）常是無法被確定的，必須了解編譯行為、以及編譯后的bytecode才能了解會發生什么事。然而一個好的程式語言，應該讓程式設計師只看高階的程式碼就能判斷會及不會發生什么行為。

什么是正規語意？以虛擬碼與Hoare Logic 為例

一個典型用Hoare Logic進行分析的程式會具有三元的結構{ P } C { Q }，不嚴謹的解釋是對于一個程式C，其執行前的狀態P（前件）會在執行后變成狀態Q（后件）。狀態P ， Q都是由命題構成集合。

我們先看一句簡單的指令：x ：= x+1

這個指令做的事很簡單，「將x加上1后賦值給自己」。但在撰寫程式時我們其實是對這個指令執行前與執行后會發生的事已經在腦內有許多的預設了，才會寫下這樣的程式。而Hoare Logic正是將這些腦內的預設寫下來。例如，若我在寫下這行程式時，我確信執行前的x的值為42，那在一個語法沒有其他作用的程式語言中，這行程式執行完x的值會變為43。在Hoare Logic中可以寫成{ x =42} x ：= x +1{ x =43}。

我們再看另一行程式

y ：= x

若在寫這行程式時我們已經想好x的值會是43，那執行完y應當要是43。寫成Hoare Logic便是{ x =43} y ：= x { y =43}。

當我們發現第一個程式的后件與第二個程式的前件相同，便能將上面兩行程式連接起來，而變成{ x =42} x ：= x +1; y ：= x { y =43}。

從而在寫一個程式時，我們若總是在每個小程式前后加上前件與后件（P與Q），最后在將所有程式組合起來時，就能確切知道這個程式在給定一個執行前的狀態下，執行后必然會發生什么事。

在設計一個語言時，若我們所有最基本的單元操作的前后件都寫出來，那就可以想像我們能設計一套工具去判斷整個程式執行前后一定會發生的事，而不會有如C 語言中的undefined behavior 或需要看bytecode 才能確定的行為。

Matching Logic 與K-framework

K Framework是一個用來定義程式語言的工具，其運用的是Hoare Logic的延伸— — Matching Logic。在K Framework中，定義一個語言需要三個基本的元件：語法（syntax）、配置（configuration）與規則（rule）。

定義程式語法用的（K的）語法是BNF，若寫過functional語言或讀過計算理論的人可能會很熟悉，簡單來說就是將一個語言中的所有可能出現的語法以遞回的方式定義清楚，以這篇論文中定義Solidity的語法方式為例子：

K ：= uintm | address | K［ n ］

T ：= uintm | address | T［ n ］ | T［］ | mapping KT| ? T ??? T ? | contract | ref T

這部分只列出所有Solidity 可能出現的型別，若要完整定義語言還需列出如contract、pragma 等關鍵字。

而Solidity 寫成K Framework 的語法實在太長了，這里就先以一個官網范例中簡單的語言IMP 為例子（簡寫自imperative，相對于declarative 語言。其實定義純functional 的declarative 語言相對簡單，也是官方提供的第一個范例，但讀者應該更熟悉如Solidity 或C 等imperative 語言因此也用此舉例）

IMP 以K Framework 定義的Syntax 如下

module IMP-SYNTAX

syntax AExp ：：= Int | Id

| AExp “/” AExp

》 AExp “+” AExp

| “（” AExp “）”

syntax BExp ：：= Bool

| AExp “《=” AExp

| “！” BExp

》 BExp “&&” BExp

| “（” BExp “）”

syntax Block ：：= “{” “}”

| “{” Stmt “}”

syntax Stmt ：：= Block

| Id “=” AExp “;”

| “if” “（” BExp “）” Block “else” Block

| “while” “（” BExp “）” Block

》 Stmt Stmt

syntax Pgm ：：= “int” Ids “;” Stmt

syntax Ids ：：= List{Id，“，”}

endmodule

由此可以看出，對于任何一個指令Stmt，他都必需是Stmt所定義的形式中其中一種。如while（1）{x=1+1;}是合法的Stmt，因為他符合“while” “（” BExp “）” Block的形式，而這是因為while中的1符合BExp的形式，而且x=1+1符合Stmt中Id “=” AExp “;”的形式，因為1+1符合AExp …依此類推。

而配置（configuration）則是將語言執行中會用到或改變的狀態（state）寫下來，這些配置可以是記憶體、計數器等。如果是完全沒有副作用的語言那可能不需要定義這種狀態（完全不需要輸入輸出的declarative 語言可能就用不到，如K Framework 在tutorial 中定義的小語言LAMBDA）。然而一般實務上使用的語言一定用到外部的狀態，狀態也能稱為環境（enviroment），可以理解為從語言中看不出來，但在執行時會用到與造成影響的對象。如在C 中直接修改記憶體的操作，雖然語法上只是一個指令（指令執行的結果在后續程式中拿來使用），但實際上對「記憶體」這個狀態造成了影響。以Solidity 來說實體的state 就是Storage 與Memory。真正需要定義的state 其實細分非常多，如Type Space（從變數名稱到Type 的對應關系）、Name Space（變數名稱到記憶體位置的對應關系）、Storage 與Memory（從記憶體位置對應到其上的值）等。

配置可以是巢狀的，也就是說一個配置中可以包含其他配置。例如一個thread 中有一個stack，一支程式可以有好幾個thread，就用得到這樣的配置。

IMP 中的configuration 長這樣：

configuration 《T》

《k》 $PGM:Pgm 《/k》

《state》 .Map 《/state》

《/T》

與龐大的語言比起來這是非常簡單的configuration。語法是XML，一個configuration的空間稱為一個cell，這里有兩個cell，k與state。k里面放的是程式碼本身，而state則儲存了如變數等需要記錄的狀態。T可以暫時不理會。$PGM是K Framework的變數，意思是程式碼要放在這個cell中（程式碼也是環境的一部分！如在C中程式碼也是data的一部分，甚至能寫出能讀寫自己的程式碼區塊的程式），：Pgm說明這個程式碼同時必須是符合Syntax中定義好的Pgm的形式才行。

configurations 也定義好后，就要寫規則。規則就是最重要的「程式如何執行」的原則。在K Framework 定義的語言中，一行指令會做出什么操作，一定要是明確寫出的一條規則才行，否則就會無法執行。一條規則的形式是「可被執行的程式」加上其「被執行成的結果」，另外能加上附加條件以及其會對環境（配置）造成的影響。如現在有條簡單的規則：

rule while （B） S =》 if （B） {S while （B） S} else {}

這條規則是在說明，任何符合while （B） S形式的語法都能執行為if （B） {S while （B） S} else {}。=》這個動作可以稱為重寫（Rewrite），因為這規則的意思其實就是「將左邊的程式重寫成右邊的程式」，再將重寫后的程式繼續依照其他規則執行（重寫）下去。

再看另一條規則：

rule 《k》 X = I:Int; =》 。 .。.《/k》 《state》。.. X |-》 （_ =》 I） 。..《/state》

這條規則是在說，在k這個configuration中，當出現X=I形式時（I必須為Int），其會被重寫為什么都沒有（。在K Framework中是nothing的意思）。在《k》 《/k》中開頭沒有 。..，結尾卻有，意思是若要使用這條規則，X=I的形式必須出現在程式的開頭。而state中X所對應到的值會被取代為I。（|-》是變數名稱與值的對應關系，_是本來所對應到的值，但因為不需要用到本來的值所以用_）

到這邊為止應該可以看出，規則跟上面講的Hoare Logic其實非常像！只是我們將前件后件寫成了Rewrite的規則，{ P } S { Q }被轉換成了S ∧ P ? T ∧ Q這樣的形式（T是Rewrite后的程式碼）。

K-framework 中被正規化的 Solidity

寫了這么多，這篇跟本還沒講和Solidity 有關的內容。的確，光是介紹K Framework 就花了很多功夫，在開頭提及的論文中，南洋理工與新加坡科技設計大學的人將Solidity 的基本語意實作在K Framework 中，寫了50 個configuration 以及200 多條rule（2000+ 行），目前已經可以在K Framework 中執行。在執行過程中，我們就能做動態的測試，判斷cell 中會不會出現預期以外的值。

我們就看其中一條簡單的rule。

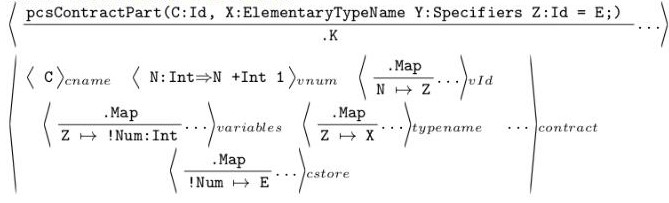
（注意這里的水平分隔上下就是? 的左右）

Elementary-TypeName這條規則中，pcsContractPart是一個定義在K Framework的函數，會被展開為一個可以被重寫的形式。（在《k》中的）程式碼若是符合一個變數宣告的形式，contract cell中的許許多多配置就能夠方式如上的操作。以uint public data = 10;為例，uint可以代入X（ElementaryTypeName）、public代入Y（Specifiers）、data代入Z（Id），10代入E。當出現符合這樣規則的程式后，這行指令的下一步可以被「重寫」為什么都不剩（.K，「。」開頭為nothing的意思）。同時，在這個程式執行時的狀態，也就是configuration中：

· cname（合約名稱）必須有符號 C

· vname （記錄變數數量）中的數字N 會增加 1

· vId （記錄第N 個變數的變數名稱）會多出一條N 到Z 的對應

· variables （從變數名稱到變數地址的對應）會多一個Z 到 ！Num 的對應，！Num 是告訴K 產生一個新的數字作為地址

· typename （記錄從變數名稱到Type 的對應）多一條Z 到X 的對應

· cstore （記錄從地址到值的對應）多一條 ！Num 到E 的對應。

需要注意的是，每個cell 中的前件都要成立，這個規則才適用。如果前件為nothing（「。」開頭），那就代表這個cell 沒有前件。例如，若contract cell 中沒有C 這個合約名稱，這條規則就不能被使用。如果一行指令沒有任何規則能被套用，程式就會執行不下去。

結語

語意正規化后，離正規驗證其實還有段距離。若我們想要驗證一個程式的正確性，我們得先將我們所認為的「正確」的條件（specification）給列出來。例如，在一個扣款的合約中，錢包被扣除的數字必須只能有一次，我們就能另外寫程式檢查在存有錢包金額的那個cell中，是不是一定只會減少某個數字。但這樣的程式要怎么寫又是另一個大工程，其中牽扯到將Matching Logic轉換成可以被驗證的邏輯模型等問題。已經有人將EVM實作在K Framework中（注意不是Solidity，在計算理論中，要描述一個完整的程式語言與描述一臺電腦是等價的，EVM同理也能以K Framework描述），并配合Z3證明器寫了用來證明Smart Contract的工具，里面附有一些已經證明好的Smart Contract與他們的specification，有興趣的人可以了解一下。