“區塊鏈應用的圣杯”,“加密世界的印鈔權”,“不受人為控制的自由貨幣”,從項目方到交易所甚至到傳統金融領域,大家都想做,人人都在聊。
提及穩定幣,一般會先介紹三種模式: 法幣托管模式、數字資產抵押模式和無抵押算法穩定幣。

?
這其中,算法穩定幣可謂是想象空間最大也是最為神秘的一種。
畢竟,用計算機代碼控制一個經濟體里的貨幣發行,沒有任何中心機構的控制,再附上人工智能的屬性,是一個極有吸引力的故事,尤其是對于加密朋克們。
然而,從嚴格的貨幣理論來看,算法穩定幣是一個偽命題。任何貨幣發行機制都是既定規則與自由裁量的權衡。僅僅依靠自動運行的算法,就如同面對一個擁有基本聊天功能的機器人,可以日常對話,但在面對更復雜的需求和突發的情況時,與完備的系統還相去甚遠。
何為算法穩定幣
與法幣托管 1:1 生成對應穩定幣 (100%的美元儲備) 和數字資產質押貸出穩定幣 (超額的數字資產儲備) 不同,算法穩定幣追求無抵押發行。
沒有資產背書,如何保障其發行貨幣的價值呢?算法穩定幣美名為模擬央行的公開市場操作 — 在穩定幣的價格高于1美元時,增加供給。在穩定幣價格低于1美元時,回收供給。
通常有兩種做法,第一種 (以 Basis 為例) 是在系統中引入“債券”和鑄幣股份 (Seigniorage Shares)。
當穩定幣的價格低于1美元時,系統會發行可以用穩定幣購買的債券,債券能夠在未來收到更多的穩定幣。通過回籠市場上穩定幣的供給,試圖將價格推動回1美元附近。
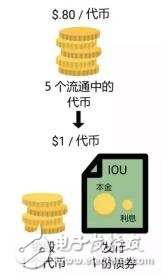
當穩定幣的價格高于1美元時,系統會給債券的持有者發放更多的穩定幣,增加市場上穩定幣的供給,將價格平復到1美元左右。
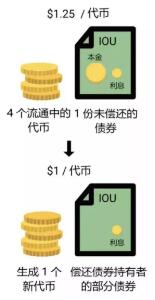
另一種做法 (以 Ampleforth 為例) 則更為簡單粗暴,當穩定幣價格高于 1 美元,會給用戶地址空投更多穩定幣。
而當穩定幣價格低于 1 美元,會自動蒸發部分穩定幣。假如目前穩定幣的價格跌到 0.5 美元,那么所有擁有該穩定幣的地址會減少一半,物以希為貴,直到穩定幣的價格回到 1 美元。
聽起來頗有經濟學道理的機制,實際上經不起推敲。
在穩定幣的價格高于1美元時,意味著市場對其樂觀,穩定幣處于溢價,增加供給可以自然降低價格。但是,在穩定幣的價格低于1美元時,表示此時市場上對該穩定幣的信心已經開始動搖。即使發行債券,承諾在未來發放更多的穩定幣,人們也沒有動力去購買持有,反而會進一步出售穩定幣。這會加大市場上穩定幣實際值與錨定值的偏差,從而使系統趨向進一步的不穩定。
通過蒸發的方式更是抱薪救火的惡性循環,不僅無法鎖住流通中的穩定幣,人們反而會擔心自己手里的穩定幣面值縮水,進而恐慌拋售,結果是價值直接歸零。
穩定幣設計的背后:規則還是自由裁量
已有項目的缺陷或許不足以代表一種模式的失敗,但是將算法作為機制的占位符,掩蓋了貨幣政策設計的核心,即謹遵規則還是自由裁量。(Rules vs Discretion)
實際上,用算法控制貨幣的發行量并不是什么新鮮事。
早在1960年,著名的諾貝爾經濟學獎獲得者弗里德曼就提出用電腦取代美聯儲,每年增加固定的貨幣數量,這后來被稱為 K 百分比準則,即每年增加 K 百分比的貨幣供給量,試圖實現穩定的價格和低失業率,解決因貨幣超發帶來的問題。
弗里德曼構想用絕對的規則替代中央銀行的自主性,因為在他看來,經濟活動的波動性來源于中央銀行貨幣政策的不確定性。
K 百分比規則是貨幣政策的剪影。規則還是自由裁量 ,這兩種主張在20世紀60年代至80年代成為學界辯論的焦點,一方認為貨幣市場不應該受到一個中央權威的政策和商業周期所左右,而應該基于既定的規則。另一方則主張更為靈活,比如反周期政策 (在繁榮時期緊縮,在蕭條時期擴張),以及在遇到無法預見的黑天鵝事件時進行緊急救助。
雖然弗里德曼用電腦替代中央銀行的設想沒能在任何國家得以實施,不過加密貨幣的世界里給了類似機制的檢驗機會。
如果說比特幣是模仿黃金的固定通縮機制,而近期引起關注的隱私幣 Grin 則是類似 K 百分比準則,每年以固定的增長量發行貨幣。


只不過,至少從現有數據來看,這種線性增長的貨幣政策并沒有帶來穩定的價值,無論是比特幣還是 Grin 都沒能實現預期的交易媒介功能。
算法穩定幣并不高明的模仿
算法穩定幣的訴求同樣是遵循規則勝于自由裁量。相比于 Grin 和比特幣,其改進之處在于采用了響應式政策,而非單一固定的規則。比如根據貨幣的市價調整貨幣的供給,反過來影響貨幣的預期價格。
貨幣供給決定貨幣價格。這一觀點來自于費雪方程式(MV = PY),即一個經濟體里的貨幣量與流通速度之積 = 商品總量×價格水平。在流通速度和商品總量相對恒定時,貨幣發行量決定物價水平。進一步推導出,只要控制貨幣的發行量,就可以決定物價水平。
需要注意,基于費雪方程式的貨幣數量理論有一個重要前提,那就是貨幣流通速度是恒定的。
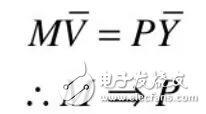
但這在高流動性的加密貨幣市場并不成立,一旦穩定幣進入市場,流通速度就不受貨幣發行方所控制。此外,費雪方程式中的貨幣量只代表高能貨幣。高能貨幣具有使貨幣供應總量成倍放大或收縮的能力。對于穩定幣而言,高能貨幣是存在于區塊鏈上的貨幣實體,但并不包括基于該穩定幣發行的影子貨幣,如交易所賬本上的余額、各種鏈上或鏈下衍生品。
對于 Ampleforth 類的穩定幣項目,想要憑空蒸發掉已經流動在市場上或者“映射”后的穩定幣供給,不僅在技術上無法做到,更是一個充滿擠兌風險的擊鼓傳花游戲。
根本原因,并不是控制了貨幣的供給量,就可以控制貨幣的價格。貨幣供給量只是經濟活動的結果,而不是貨幣政策手段,僅僅關注貨幣的供給量是舍本求末。
除了貨幣供給量之外,還有什么變量會影響貨幣的價格穩定呢?利率是重要的因素之一。而帶有鑄幣股份和債券的算法穩定幣本質上是模擬一個可貸資金市場 - 貨幣市場 + 債券市場。
使用利率控制經濟體里的通脹水平其實并非天方夜譚,經濟學人熟知的泰勒規則,被很多國家貨幣當局視為政策參考標準。

簡單來說,這一規則根據當前 GDP 與潛在 GDP 水平之差以及當前通脹水平與預期通脹率之差,去調整基準利率,從而幫助一個國家實現經濟產出增長和物價的穩定。
那么,為何在傳統世界被廣為借鑒和采用的規則,放在區塊鏈和加密貨幣上就行不通呢?
在于算法央行買賣債券與傳統央行的公開市場操作有著很大區別。
其一,美聯儲出售和回購美元是相對于國債,而不是所謂的“央行債券”。國債背后是稅收的收入支撐,央行債券名義上只是在未來發放貨幣的承諾。沒有商業和貿易的穩定幣孤島,是很難產生收入來源的。
其二,債券之所以可以承諾未來支付高于市值的貨幣,是因為債券的流動性是低于貨幣的。債券有著不同的償還期限,以及根據期限管理的現金流。而鑄幣股份模式下,債券和穩定幣本身的流動性是一樣的,沒有期限,先到先得。
這兩點意味著,算法穩定幣所謂的“債券”實際上只是期貨。
此外,鑄幣稅的前提是該貨幣是經濟體中用來支付稅務的唯一法定貨幣,外國貨幣和私人貨幣都無法參與。而加密貨幣的出發點是增加貨幣之間的競爭,不限制私人貨幣的發行和流通。
因此,在市場單邊下行時,人們可以自由地將貶值中的算法穩定幣出售成其他的加密貨幣或法幣,而本應作為回收穩定幣的兜底債券,將會形成流動性更高的期貨市場,造成螺旋式崩盤。
唯有抵押穩定幣具備長久價值
目前,在加密貨幣的市場上,只有具備抵押的穩定幣才有長久的價值。

為什么這么說?因為貨幣發行方,無論是一串代碼又或是 DAO,都不與現實中的身份和權益掛鉤,也就無法創造沒有擔保的信用貨幣。那么誰來甄別有能力借貸還款的個人和機構,誰來在他人違約破產時清算資產和緊急救助?
即使算法穩定幣引入部分資產作為抵押品,就發行機制而言,即要有合適的規則讓交易多方有穩定的預期,也要能夠根據特殊情況隨機應變。要實現這些,人為的判斷和鏈下的治理不可避免。
此外,在貨幣政策中引入數據分析,其實在傳統銀行體系已經被大量采用,各國的中央銀行和商業銀行通過指標收集反饋和預測模型,幫助在不同貨幣政策中選擇最合適的工具。
制定一個經濟體的貨幣政策,不亞于在錯綜復雜的地形里駕駛一臺高速前進的汽車,即使裝備了最先進的自動駕駛系統,也需要警察和防護人員在機器犯傻時人為參與。而一味地在基礎設施不完備、身份數據欠缺的區塊鏈上強調某種神奇的穩定貨幣算法,無異于在 Excel 上訓練自動駕駛汽車模型,是遠遠不夠用的。
 電子發燒友App
電子發燒友App





















評論