如何搞定機器學習中的拉格朗日?看看這個乘子法與KKT條件大招
大小:0.4 MB 人氣: 2017-12-06 需要積分:1
拉格朗日乘子法是一種尋找多元函數在一組約束下的極值方法,通過引入拉格朗日乘子,可將有m個變量和n個約束條件的最優化問題轉化為具有m+n個變量的無約束優化問題。在介紹拉格朗日乘子法之前,先簡要的介紹一些前置知識,然后就拉格朗日乘子法談一下自己的理解。
1.梯度
梯度是一個與方向導數有關的概念,它是一個向量。在二元函數的情形,設函數f(x,y)在平面區域D內具有一階連續偏導,則對于每一點P(x0,y0)∈D,都可以定義出一個向量:fx(x0,y0)i+fy(x0,y0)j ,稱該向量為函數f(x,y)在點P(x0,y0)
的梯度。并記作grad f(x0,y0) 或者?f(x0,y0),即 grad f(x0,y0) = ?f(x0,y0) = fx(x0,y0)i+fy(x0,y0)j=(fx(x0,y0),fy(x0,y0)) 。
再來看看梯度和方向導數的關系:如果函數f(x,y)在P(x0,y0)點可微,el = (cosα,cosβ)是與方向L同向的單位向量,則?f/?L|(x0,y0) = fx(x0,y0)cosα+fy(x0,y0)cosβ = grad f(x0,y0).el = |grad f(x0,y0)|.cosθ ,其中θ表示的梯度與el 的夾角。由此可知,當θ = 0時,el 與梯度的方向相同時,此時方向導數最大,函數f(x,y)增長最快;當θ = π時,el 與梯度的方向相反時,此時方向導數最小且為負,函數f(x,y)減小最快。
2.等高線(等值線)
通常來說,二元函數 z = f(x,y)在幾何上表示一個曲面,這個曲面被平面 z = c(c為常數)所截得的曲線L的方程為:

這是一條空間曲線,這條曲線L在xOy平面上的投影是一條平面曲線L*,它在xOy平面直角坐標系中的方程為:f(x,y) = c 。對于曲線L*上的一切點,已給函數的函數值都是c,所以我們稱平面曲線L*為函數z = f(x,y)的等值線(等高線)。再來看看等高線的一些性質:
若fx,fy不同時為零,則等高線 f(x,y) = c上任一點P(x0,y0)處的一個單位法向量為:
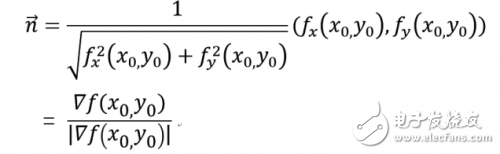
這表明函數f(x,y)在一點(x0,y0)的梯度?f(x0,y0)的方向就是等高線f(x,y) = c在這點的法向量的方向,而梯度的模|?f(x0,y0)|就是沿這個法線方向的方向導數?f/?n,于是有:

非常好我支持^.^
(0) 0%
不好我反對
(1) 100%
