引言
實際光學系統的成像是不完善的,光線經光學系統各表面傳輸會形成多種像差,使成像產生模糊、變形等缺陷。像差就是光學系統成像不完善程度的描述。光學系統設計的一項重要工作就是要校正這些像差,使成像質量達到技術要求。光學系統的像差可以用幾何像差來描述,包括:

?預備知識:
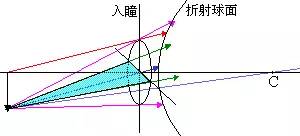
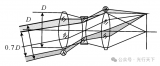
主光線:某視場點發出的通過入瞳中心的實際光線
第一近軸光線:軸上物點A發出的通過入瞳邊緣點的“近軸”光線
第二近軸光線:軸外某視場點發出的通過入瞳中心的“近軸”光線
子午平面:包含物點和光軸的平面稱子午平面
弧矢平面:包含主光線并與子午平面垂直的平面稱弧矢平面
輔軸:軸外點和球心的連線稱為該折射球面的輔軸
上光線:軸外點發出通過某孔徑帶上邊緣的光線稱某孔徑帶的上光線
下光線:軸外點發出通過某孔徑帶下邊緣的光線稱某孔徑帶的下光線
前光線:軸外點發出通過某孔徑帶前邊緣的光線稱某孔徑帶的前光線
后光線:軸外點發出通過某孔徑帶后邊緣的光線稱某孔徑帶的后光線
想一想:你能在圖中找出對應光線或平面嗎?
正弦條件和等暈條件
?正弦條件
首先我們考慮離光軸很近的軸外點,稱近軸軸外點。
設軸上物點A→A’能以任意寬光束完善成像,則垂軸方向的近軸軸外點B→B’也能以寬光束完善成像需滿足的條件稱正弦條件。
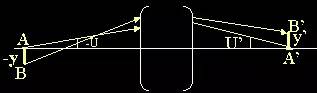
正弦條件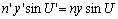 , , |
也可寫成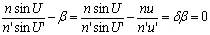 |
當物距為無窮遠時,經公式變換,可將正弦條件寫成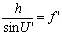 。
。
可以證明,齊明點滿足正弦條件。
等暈成像和等暈條件
實際由于球差存在,只能要求近軸軸外點具有和軸上點A相同的成像缺陷。此時稱等暈成像,需要滿足的條件稱等暈條件:

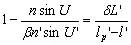 |
當物在無窮遠時化為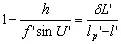 |
當球差為零時,等暈條件化為正弦條件。
當不滿足等暈條件時,軸上點與近軸軸外點成像缺陷不等,用正弦差表示:
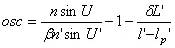 |
當物在無窮遠時有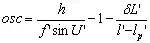 |
正弦差與孔闌位置有關,當球差不為零時,可以找到某孔闌位置使正弦差為零。
正弦差表征光學系統不滿足等暈條件的程度。當正弦差不為零時,軸外點存在彗差。
軸外像差
由于折射球面存在球差和像面彎曲,使軸外點衍生出一系列像差。
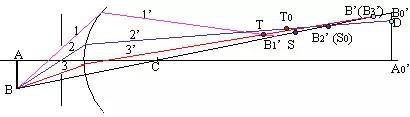

| 局部放大可畫出各種軸外像差 |
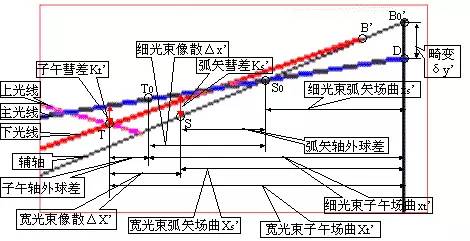
彗差
當系統不滿足等暈條件時,軸外點存在彗差。
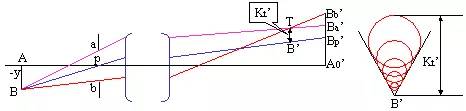
上下光線的交點偏離主光線:子午彗差
前后光線的交點偏離主光線:弧矢彗差
| 利用這些光線與高斯像面的交點高度來計算,其中前后光線關于子午面對稱,它們與理想像面的交點高度必相等 |
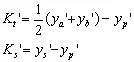 |
各環帶上下、前后光線的會聚點相對于主光線不同,孔徑大的偏離大,靠近主光線的偏離小,所以僅有彗差時,將形成彗星狀的彌散斑。
不同孔徑U有不同的彗差,不同視場W有不同的彗差,所以彗差和孔徑、視場都有關。
像散和像面彎曲
對于寬光束,軸外主光線和共軸系統的光軸不重合,使出射光束失去對稱,產生彗差、像散和像面彎曲;
對于細光束,彗差為零,但像散和像面彎曲仍然存在。
子午細光束像點在主光線上,弧矢細光束像點在主光線和輔軸的交點上,兩者之軸向距離為像散。當視場由小變大時,子午細光束像點和弧矢細光束像點會偏離高斯像面。如果把各視場的子午細光束像點或弧矢細光束像點連起來,將會得到彎曲的像面,這就是像面彎曲。
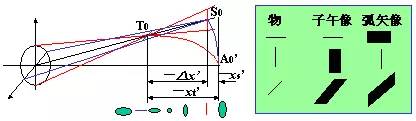
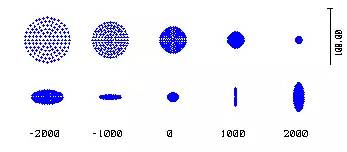
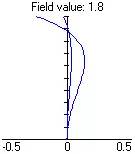
| 左圖是對某具有很大像散和像面彎曲的光學系統的計算結果,表示了不同位置處的軸上點與軸外點單色光彌散斑,第一行是軸上點產生的彌散斑,第二行是軸外點產生的彌散斑,第三行數字表示位置,單位是微米。 |
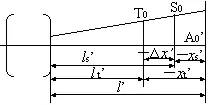
計算一條主光線,即可按下式計算并畫出像散與像面彎曲曲線:
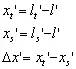 |
 |
|
| 本圖形由軟件GA畫出 |
曲線中縱軸是視場,橫軸是像面彎曲。將子午像面彎曲(用T表示)和弧矢像面彎曲(用S表示)畫在一起,即可知道像散,不必另畫像散曲線。
想一想:若像散為零,像面彎曲是否存在?
像散為零時,子午細光束像點和弧矢細光束像點重合,但不與高斯像面重合,所以像面彎曲仍然存在,這種像面彎曲叫匹茲凡面彎曲。
畸變
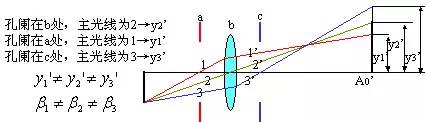
由圖可見,當孔闌位置移動,主光線與高斯像面交點高度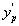 變化,引起像的變形。
變化,引起像的變形。
畸變僅是像的變形,不影響像的清晰度。有些光學系統只對清晰度要求高,對變形的要求可以降低。
實際像高比理想像高大,稱正畸變,反之稱負畸變。根據畸變的正負,等距的同心圓將會變成不同形狀的不等距的同心圓,正方網格也會變成枕形或桶形。
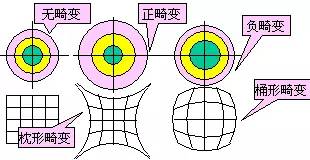
可用絕對畸變或相對畸變來度量畸變的大小。
絕對畸變又稱線畸變: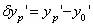 ?? ? ? ? ? ? ? ?? ? ? ? ? ? ?相對畸變是實際放大率與理想放大率的相對誤差: 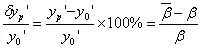 畸變曲線如右圖。 |
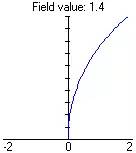 |
| 本圖形由軟件GA畫出 |
畸變特征:
1.全對稱系統(結構對稱,物像對稱),不產生畸變;
2. 孔闌與之重合的接觸薄系統,不產生畸變(主光線通過系統中心,沿理想方向射出);
3. 對于單薄透鏡,光闌前移——負畸變,光闌后移——正畸變。因此,畸變與光闌位置有關。
初級軸外像差
光學系統的初級軸外像差也可以用賽得和數來表示。一共有5個賽得和數。除了球差部分的第一賽得和數外,還有第二賽得和數至第五賽得和數,它們分別是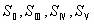 。
。
| 初級彗差 | |
| 初級像散與像面彎曲 |
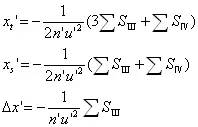 |
| 初級畸變 |
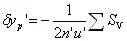 |
| 其中 |
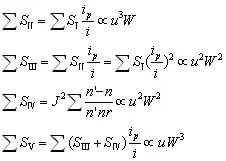
所以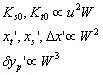 |
匹茲凡面彎曲
當像散為零即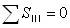 時,仍有
時,仍有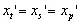 ,稱為匹茲凡面彎曲。
,稱為匹茲凡面彎曲。
這里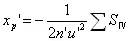 ,
,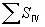 即第四賽得和數也叫匹茲凡和。
即第四賽得和數也叫匹茲凡和。
下面通過分析簡單系統的匹茲凡和研究匹茲凡和的校正方法。
單個薄透鏡的匹茲凡和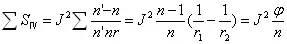
①單薄透鏡的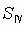 由 由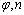 所決定 所決定 |
②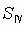 與 與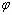 同號,與薄透鏡形狀無關。一般 同號,與薄透鏡形狀無關。一般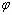 不為零。所以單薄透鏡不能校正匹茲凡和。 不為零。所以單薄透鏡不能校正匹茲凡和。 |
薄系統的匹茲凡和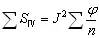
接觸的薄系統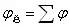 |
一般總光焦度>0,折射率相差不大,匹茲凡和不可能為零。 |
分離的薄系統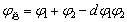 |
正正分離對校正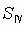 更不利,正負分離可校正 更不利,正負分離可校正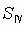 |
單厚透鏡的匹茲凡和
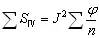 中 中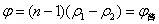 |
實際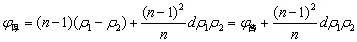 |
若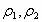 同號使 同號使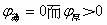 ,則可校正匹茲凡和。 ,則可校正匹茲凡和。 |
設該厚透鏡要校正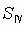 |
則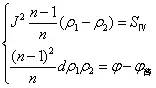 |
 |
| 這樣一塊厚透鏡可看成正透鏡+平板+負透鏡 | ||
|
結論:正負光焦度的分離是校正匹茲凡和的唯一方法 |
-
曲線
+關注
關注
1文章
82瀏覽量
20843 -
光學系統
+關注
關注
4文章
240瀏覽量
18289 -
清晰度
+關注
關注
0文章
7瀏覽量
6903
發布評論請先 登錄
相關推薦
全固態Nd:YAG激光器熱效應及輸出光束波前像差分析
頭盔顯示器設計參數簡析
GLAD案例索引手冊
[VirtualLab] 不同像差的焦點
人眼波像差測量中形心探測的新方法
單色像差有哪些分類
大視場超光譜成像差分吸收光譜儀光譜定標裝置的原理及設計
如何防止光學像差/減少光學像差的負面影響
利用高級球差曲線分析光學系統
光學系統設計的不可忽略的參數介紹
機器視覺鏡頭的成像機理與特性解析
遠心鏡頭的幾個參數解析





 關于像差概論-軸外像差的分析和介紹
關于像差概論-軸外像差的分析和介紹










評論