本例電路使用LM324運放設計一款方波,三角波,正弦波的函數信號發生器。

電路分解:
整個電路的模塊劃分很明顯,其結構如下:
一是由U1A和外圍電阻,穩壓管組成的遲滯比較器,產生方波信號;
二是由U1B組成的積分電路,產生三角波信號;
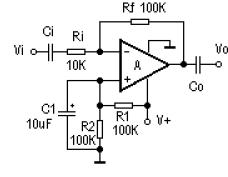
三是由U1C以及外圍電阻電容組成的一階低通有源濾波器,產生正弦波。
整個電路的工作過程如下:
電路中方波發生器和三角波發生器首尾相接,形成一個正反饋閉環系統。比較器U1A輸出的方波經積分器U1B輸出可得三角波,三角波又觸發比較器自動翻轉形成方波,這樣即可構成三角波,方波發生器。同時,本例電路中,是采用運放組成的積分電路,因此可實現恒流充電,使三角波線性大大改善。
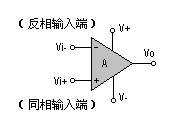
用比較通俗的話來講就是當比較器輸出使比較器的同相端電壓高于0V時,比較器U1A輸出翻轉到高電平,即Uz+0.7V;當比較器的輸出使比較器的同相端電壓低于0V時,比較器U1A輸出翻轉到低電平,即-(Uz+0.7V)。
這樣,當比較器輸出高電平時,三角波的輸出是向負向變化;當比較器輸出為低電平時,三角波輸出向正向變化。
這樣不斷的重復,就得到了三角波和方波。
其中方波的幅值受穩壓管限制;而三角波的幅值大小為R8*Uz/R5。這個具體怎么得來的,可根據運放的虛短和虛斷原理來計算。
正弦波輸出原理如下:
三角波展開為傅立葉級數可知,它含有基波和3次、5次等奇次諧波,因此通過低通濾波器取出基波,濾除高次諧波,即可將三角波轉換成正弦波。
但是低通濾波器的通帶截止頻率應大于三角波的基波頻率且小于三角波的三次諧波頻率。
圖中U1C就是一個常見的反相輸入一階低通濾波器。實際上就是一個積分電路,其分析方法與一階積分電路相似,但又與積分電路有不同的地方,下面是從網上所查到的關于這兩者的一個分析,供大家參考:
某些文獻上將積分器與RC低通濾波器混為一談,但是,兩者并不相同。
從傳遞函數上看:
積分器的傳遞函數是:Vout/Vin=ω0/s,而一階RC低通濾波器的傳遞函數是:Vout/Vin=ω0/(s+ω0)。
可見,當信號頻率遠遠高于ω0對應頻率時,兩者特性相當,也就是說,在高頻衰減特性上,兩者非常類似。
但是,對于低頻的”低通“特性上,兩者有本質的區別,信號頻率低于ω0對應頻率時,尤其是信號為直流時,低通濾波器輸出等于輸入,而積分器輸出隨時間變化,將上升至電路允許的電壓上限(理想積分器將到無窮大)。
應該說,積分器與低通濾波器的高頻特性基本相同,而低頻特性有本質區別。
注意:
要想更好的理解本例電路,應該從數學計算入手,分析不同的輸出函數受什么影響,然后根據這些分析來調節所得波形的一些參數,比如頻率,幅值,相位等。
-
LM324
+關注
關注
15文章
166瀏覽量
65019 -
函數信號發生器
+關注
關注
6文章
68瀏覽量
14382
發布評論請先 登錄
相關推薦
運放LM324失效
LM324 四運放集成電路的應用




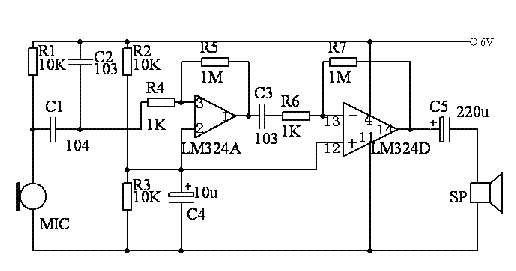
 使用LM324運放設計的函數信號發生器電路
使用LM324運放設計的函數信號發生器電路










評論