在哥倫比亞（Christopher Columbus）航行前，所有人都認(rèn)為地球是平的… 。在過去的許多年中，我將傳統(tǒng)的史密斯圓圖進(jìn)行擴(kuò)展來幫助我理解射頻領(lǐng)域中像振蕩器設(shè)計(jì)以及放大器的穩(wěn)定性這類涉及到負(fù)阻抗器件的問題。其概念使得我對于與阻抗有關(guān)問題的本質(zhì)有了更深的理解，并且也證明了這是一個(gè)很有用的附加的設(shè)計(jì)輔助工具。最近，在餐桌上與其他工程師討論時(shí)，我提到了自己的一些想法。這些想法得到了大家的認(rèn)可，從那時(shí)起，他們多次說服我將自己對史密斯圓圖的擴(kuò)展發(fā)表出來。為此，在這篇文章中，我試圖用最簡單的方法來解釋基于眾所周知的史密斯圓圖基礎(chǔ)上的概念性輔助設(shè)計(jì)工具背后的思想。

史密斯圓圖的最大優(yōu)點(diǎn)在于它實(shí)際上是一個(gè)“圖形計(jì)算器”。可以通過在史密斯圖上畫線來獲得阻抗匹配的結(jié)果，而無需進(jìn)行冗長的數(shù)學(xué)計(jì)算。所有工程師都可以使用這個(gè)工具，并且能幫助他們開發(fā)對可 選擇的匹配網(wǎng)絡(luò)的 直覺認(rèn)識。確實(shí)，當(dāng)一個(gè)工程師對史密斯圓圖開始理解，并且在他的腦海中有一個(gè)史密斯圓圖時(shí)，便有可能預(yù)先將潛在的匹配方案直觀化。

本文所討論的史密斯圓圖的擴(kuò)展是將平面二維（2-D）的圓圖（例如一片紙或計(jì)算機(jī)屏幕）移到一個(gè)球面的三維圓圖（3-D ）上。這種形式的史密斯圓圖可以很方便地來處理整個(gè)阻抗區(qū)域。當(dāng)然，這個(gè)新的3-D 史密斯圓圖也可以通過使用合適的坐標(biāo)變換和三維坐標(biāo)體系而用數(shù)學(xué)式子表達(dá)出來；然而，這個(gè)工作超出了本文的范圍。

已經(jīng)存在一些所謂的3-D 史密斯圓圖。但這些圖基本上是標(biāo)準(zhǔn)的二維史密斯圓圖，只是將輪廓上的數(shù)據(jù)轉(zhuǎn)換到一定高度的第三維上。據(jù)作者所知，本文所做的工作才是第一個(gè)真正的三維史密斯圓圖。該三維圓圖的實(shí)現(xiàn)是在使用了一個(gè)球體和球型坐標(biāo)體系的基礎(chǔ)上完成的。

本文假設(shè)讀者對史密斯圓圖已經(jīng)有了基本的了解。我們不打算在這里補(bǔ)習(xí)有關(guān)史密斯圓圖的知識。有許多關(guān)于傳輸線理論和射頻匹配的書籍可供讀者參考。例如，參考文獻(xiàn)[1]，[2]。本文刻意地保持描述的簡單性，避免使用令人恐懼的數(shù)學(xué)表達(dá)式。

史密斯圓圖的起源

史密斯圓圖是由Philip H.Smith 提出和開發(fā)的。文獻(xiàn)[3]介紹了Philip H.Smith 的生平。史密斯曾經(jīng)在新澤西州的貝爾電話實(shí)驗(yàn)室工作。在他作為傳輸線工程師為實(shí)驗(yàn)室工作期間，史密斯發(fā)表了2 篇有關(guān)他所做工作的重要文章[4]，[5]。圖1 便是眾所周知的史密斯圓圖。

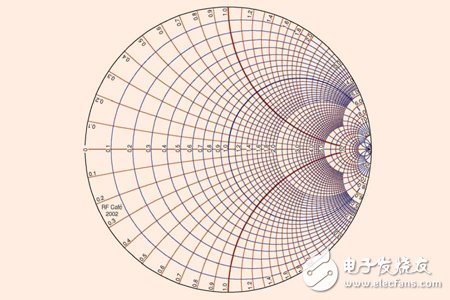
圖1、傳統(tǒng)的歸一化的史密斯阻抗圓圖（圖形由RF Café2002 提供）

最早的史密斯圓圖是作為紙上計(jì)算的輔助工具的。可以購買到已經(jīng)預(yù)先印刷好的圓圖卡片。設(shè)計(jì)工程師們隨后便可以通過使用鉛筆，尺子和圓規(guī)來完成阻抗匹配的工作。近來，射頻設(shè)計(jì)工作幾乎完全是在使用計(jì)算機(jī)的基礎(chǔ)上進(jìn)行的。精密的計(jì)算機(jī)輔助（CAD）工具可以解決難度更大的問題并且減少了設(shè)計(jì)時(shí)間。然而，廣泛使用的CAD 并沒有減少史密斯圓圖的使用率。設(shè)計(jì)軟件可以將結(jié)果在史密斯圓圖上顯示出來。類似地，現(xiàn)代網(wǎng)絡(luò)分析儀也可以將測量結(jié)果以圖形形式顯示在史密斯圓圖上。

局限性

史密斯圓圖的使用有許多吸引人的特點(diǎn)。這些特點(diǎn)包括簡潔和易于使用，這是因?yàn)樗鼘?shù)字問題轉(zhuǎn)化為圖形問題，并且所有實(shí)部為正數(shù)的阻抗都可以在一個(gè)圖上或一片紙上顯示出來。但是傳統(tǒng)的史密斯圓圖有一個(gè)很大的局限。即涉及到負(fù)實(shí)部半邊的阻抗域的處理。在將正的電阻域部分映射到清晰的圓周時(shí)（史密斯圓圖的本質(zhì)）所涉及的坐標(biāo)變換過程中，負(fù)實(shí)數(shù)部分被擴(kuò)展了。這便使得在畫出具有負(fù)實(shí)數(shù)阻抗時(shí)就會(huì)有問題了。此外，-50Ω 點(diǎn)在半徑為無窮大的圓周上。在史密斯圓圖上表示負(fù)阻抗時(shí)會(huì)很尷尬。例如，在射頻放大器設(shè)計(jì)和穩(wěn)定化過程中需要觀察穩(wěn)定性圓周時(shí)。相對于史密斯圓圖的尺寸來說，這些穩(wěn)定性圓周的圓心和半徑很容易使得圓周變得特別大。圖2 就是這樣一個(gè)例子。計(jì)算機(jī)設(shè)計(jì)軟件可以自動(dòng)調(diào)節(jié)圓圖的坐標(biāo)軸，可以將實(shí)數(shù)阻抗尺寸減到只有幾個(gè)像素那么大。另一種方法是將穩(wěn)定性圓周的圓心和圓周畫在史密斯圓圖的可視區(qū)域之外。

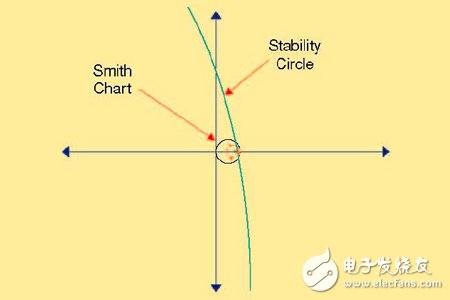
圖2、一個(gè)大的穩(wěn)定性圓周的例子

涉及到負(fù)電阻的另一個(gè)射頻/微波設(shè)計(jì)領(lǐng)域是振蕩器和微波有源濾波器的設(shè)計(jì)。在振蕩器設(shè)計(jì)中，通過使用某種串聯(lián)或并聯(lián)反饋而有意識地使得有源器件處于不穩(wěn)定狀態(tài)。由此所產(chǎn)生的負(fù)電阻與諧振電路相連接。在有源濾波器的設(shè)計(jì)中，產(chǎn)生負(fù)電阻的目的是為了試圖補(bǔ)償L 和C 元件的寄生電阻的損耗。在這兩種情況下，用圖形法來理解阻抗變換或負(fù)載是如何影響負(fù)阻抗已被證明是很有用的。

我發(fā)現(xiàn)在涉及到負(fù)電阻時(shí)，用一個(gè)三維球面而不是二維圓周的方式來表示史密斯圓圖時(shí)，可以更好地洞察匹配問題的實(shí)質(zhì)。在下一節(jié)中，我將要討論一種把阻抗域的負(fù)實(shí)數(shù)部半邊結(jié)合進(jìn)入擴(kuò)展的史密斯圓圖的有效方法。

需要注意的是，本文中使用的都是50Ω 史密斯阻抗圓圖。雖然本文在此沒有進(jìn)行展示，但也可以生成球面形的史密斯導(dǎo)納圓圖甚至球面形的并且適合于任意阻抗的混合阻抗/導(dǎo)納圓圖。

史密斯圓圖的擴(kuò)展方法

復(fù)數(shù)形式的阻抗Z=R+jX 表示在圖3 的X-Y 平面上。在這個(gè)圖形中，使用字母來代表不同點(diǎn)的阻抗。A= -∞+0j，B= -50+0j，C=0+0j，D=50+0j 以及E=∞+0j。同樣F=0-∞j，G=0-50j，H=0+50j 以及J=0+∞j。此外，R=50Ω 是用垂直虛線畫出，X=50Ω 是用水平橫虛線畫出的。可以看出在X-Y 平面的左半邊，R 小于零（因此可以表示負(fù)電阻），X-Y 平面的右半邊代表正的電阻。將阻抗平面進(jìn)行轉(zhuǎn)換就生成了圖4 的史密斯圓圖。坐標(biāo)體系轉(zhuǎn)換的詳細(xì)內(nèi)容見[1]。從圖4 可以看出，點(diǎn)E，F(xiàn) 和J現(xiàn)在都在圓周的右邊。代表電阻和感抗為零的原點(diǎn)C 是在圓周的左邊。而代表-50j 的電容和+50j 的電感的G 和H 則分別在圓周的底部和頂端。現(xiàn)在含有正實(shí)部半邊的阻抗面（R>0）是在組成史密斯圓圖的圓周內(nèi)，而含有負(fù)實(shí)部半邊的阻抗面（R<0）則在圓周之外。

圖3 所示的是代表了電阻為常數(shù)和感抗為常數(shù)時(shí)的阻抗虛線，也同樣顯示在圖4 中。遺憾的是，在系統(tǒng)坐標(biāo)變換時(shí)，具有負(fù)實(shí)部半邊的阻抗域部分被擴(kuò)展了。所以，采用史密斯圓圖來處理負(fù)阻抗就變得很棘手。

圖3、阻抗平面

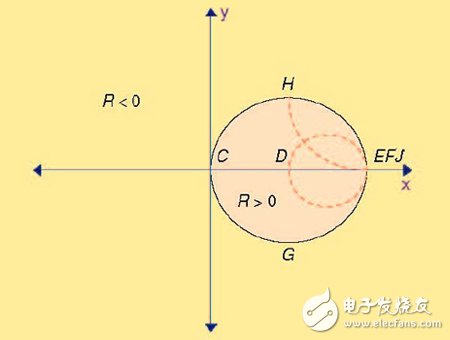
圖4、按照史密斯的方法，將正實(shí)部的阻抗平面轉(zhuǎn)換到圓內(nèi)

一個(gè)能將含有負(fù)實(shí)部半邊的阻抗平面域壓縮為易于處理的尺寸范圍的可行方法是生成兩個(gè)肩并肩的史密斯圓圖[6]，一個(gè)圓圖處理含有正實(shí)部半邊的阻抗域，另一個(gè)處理含有負(fù)實(shí)部半邊的阻抗域。這兩個(gè)肩并肩的史密斯圓圖可以幫助工程師一眼就能看到整個(gè)阻抗范圍。圖5 便是這樣一個(gè)例子。

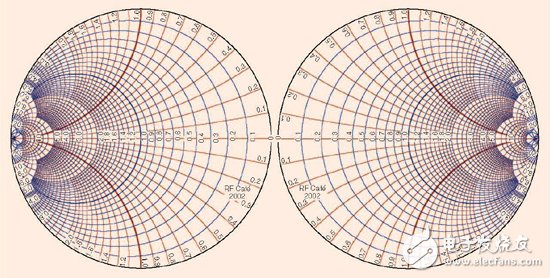
圖5、一個(gè)肩并肩的可覆蓋整個(gè)阻抗平面的史密斯圓圖（圖形由RF Café2002 提供）

肩并肩史密斯圓圖的生成是通過采用2 個(gè)坐標(biāo)變換來實(shí)現(xiàn)的，一個(gè)變換是在阻抗平面的右邊，即史密斯已經(jīng)完成了的，另一個(gè)在左邊，是含有負(fù)電阻半邊的阻抗平面部分。

參考圖3，可以看出在Y 軸上的點(diǎn)F，G，H 和J 在y 軸上從而組成了阻抗平面2 個(gè)半邊的邊界線。因此，在使用2 個(gè)坐標(biāo)變換來生成2 個(gè)史密斯圖時(shí)，這些點(diǎn)顯示在對偶處。例如，對G 來說，產(chǎn)生圖6 的對偶點(diǎn)G 和G′。因此這種方法的缺點(diǎn)是在兩個(gè)圖中，每個(gè)圖的邊界存在不連續(xù)性。例如，+50jΩ 同時(shí)出現(xiàn)在兩個(gè)史密斯圓圖中，它們之間存在一個(gè)間隔。

圖6、將整個(gè)阻抗平面轉(zhuǎn)換為兩個(gè)肩并肩的圓

這個(gè)問題的解決辦法之一是想像出兩個(gè)背靠背的史密斯圓圖，每個(gè)史密斯圓圖的外邊界相重疊。這樣一個(gè)例子可以想像為將具有正實(shí)部的阻抗和具有負(fù)實(shí)部的史密斯圓圖印刷在乒乓球拍的兩面。但是從一面變換到另一面時(shí)，同樣沒有一個(gè)平滑的過渡。這樣一來，設(shè)計(jì)工程師們就需要反復(fù)地將球拍翻來翻去。

在過去的許多年中，我將傳統(tǒng)的史密斯圓圖進(jìn)行擴(kuò)展來幫助自己理解射頻領(lǐng)域中像振蕩器設(shè)計(jì)以及放大器的穩(wěn)定性這類涉及到負(fù)阻抗的問題。

史密斯圓圖的球面擴(kuò)展形式

為了生成球形的史密斯圓圖，需將圖3 所示的整個(gè)阻抗域包圍在球體的表面。見圖7。圖3 中標(biāo)記的點(diǎn)也同樣地標(biāo)在了球面上。可以看出，圖3 的原點(diǎn)（點(diǎn)C）現(xiàn)在是在球體的左邊。其歸一化的坐標(biāo)（x，y，z）為（-1，0，0）。（注意，為了方便起見，對圖3 的原點(diǎn)作了x=-1 的偏移。）點(diǎn)A，E，F(xiàn) 和J，即在x 和y 軸上阻抗趨于正無窮大和負(fù)無窮大的點(diǎn)，現(xiàn)在的坐標(biāo)都為（1，0，0）。代表-50Ω 和+50Ω 的點(diǎn)B 和D，現(xiàn)在分別在點(diǎn)（0，0，-1）和（0，0，1）處。類似地，代表-50 j 和+50 j 的點(diǎn)G，H，現(xiàn)在分別在（0，-1，0）（0，1，0）處。

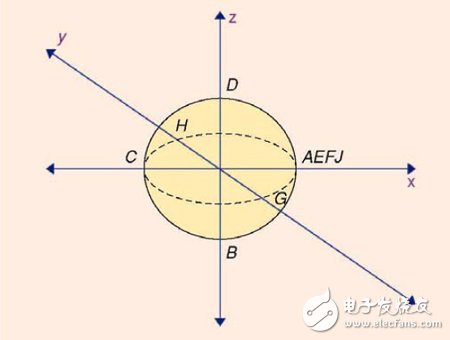
圖7、轉(zhuǎn)換到球體的表面后的阻抗平面

在這個(gè)新形式的史密斯圓圖中，阻抗為0 和無窮時(shí)的點(diǎn)在x 軸上。從Z 軸的正方向去看球體，可以看到一個(gè)類似于傳統(tǒng)的史密斯圓圖。當(dāng)然，由于球面的曲線特性，這個(gè)圓周的形狀似乎有些變形。當(dāng)把阻抗平面映射到球面上時(shí)，整個(gè)平面都在一個(gè)易于處理的區(qū)域內(nèi)，而且正電阻到負(fù)電阻的過渡可以平滑連續(xù)地進(jìn)行。

Z>0 的半球表面含有所有具有正電阻的阻抗，Z<0含有所有具有負(fù)電阻的阻抗。類似地，y>0 的半球含有感抗阻抗，y<0 的半球含有容抗阻抗。只有在球面上的點(diǎn)才有意義；在球體內(nèi)的點(diǎn)則無關(guān)緊要。

現(xiàn)在球形的史密斯圓圖已經(jīng)建成了，正如2-D 史密斯圓圖一樣，我們可以考慮不同阻抗的表示方式。

首先，電阻為常數(shù)和感抗為常數(shù)的線可以先畫出來。這些線形成了一系列封閉的圓周，起始和中止于點(diǎn)（1，0，0）。例如，+50，+50j，-50，-50j 這些常數(shù)電阻和感抗線都從點(diǎn)AEFJ（北極）開始，再回到起點(diǎn)前，跨經(jīng)點(diǎn)D，H，B 和G（在赤道上）。畫出其它值的電阻和電抗線使其類似于2-D 史密斯圓圖。見圖8。圖8（a）是從南極（z=0）看過去的球形史密斯圖，而圖8（b）是從北極（z=∞）看過去的史密斯球。

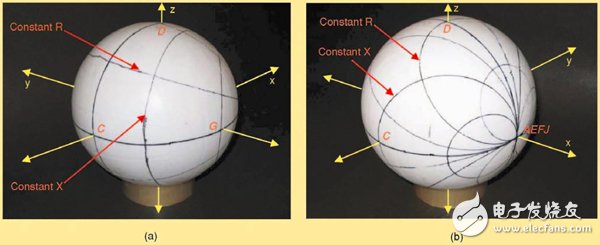
圖8、畫有常數(shù)電阻和感抗的球形史密斯圓圖 （a）從南極看過去的球體（b）從北極看過去的球體

我們還可以考慮將常數(shù)Q（品質(zhì)因數(shù)）的線畫在標(biāo)準(zhǔn)史密斯圓圖上。這會(huì)形成阻抗從零到無窮大的一系列弧線。當(dāng)Q=0 時(shí)（理想的電阻），弧線便成為一條從零到無窮大的直線，當(dāng)Q 為無窮大時(shí)（一個(gè)理想的電感或電容），弧線是沿著史密斯圖的圓周線的。在球形的史密斯圓圖上，Q 為常數(shù)的線便形成了從北極Z=無窮大到南極Z=0 的弧線。見圖9。在x-y 平面上的Q 等值的圓周上具有一個(gè)零值，同時(shí)在x-y 平面上的具有一個(gè)Q 為無窮大的Q 等值圓周。使用球形史密斯圓圖，當(dāng)電阻為負(fù)的時(shí)候，也可以很容易地使用Q 線。圖9 中增加了緯線。這些緯線是由|Z|為常數(shù)時(shí)所形成的。赤道線代表的是|Z|=50Ω。

圖9、繪有常數(shù)Q（實(shí)線）和常數(shù)|Z|（虛線）的球形史密斯圓圖

在球體中將Q 看作經(jīng)線，而將|Z|看作緯線相當(dāng)于用極坐標(biāo)而不是用迪卡爾坐標(biāo)來表示史密斯圓圖，其中mag(Z) （幅值）= Sqrt(R²+X²) ，phase(Z) （相位）=arctan(X/R) = arctan(Q)。

當(dāng)用到反射系數(shù)時(shí)，史密斯圓圖也同樣很有用。反射系數(shù)ρ 在史密斯圓圖上的表示通常是針不同常數(shù)的|ρ|的值來繪出對應(yīng)的曲線。這便會(huì)形成一系列的同心圓，圓心在傳輸線的特性阻抗點(diǎn)處（ 我們這里用的是50Ω）。這些同心圓在史密斯圓圖的中心點(diǎn)處從半徑為零開始，逐漸增加直至反射系數(shù)為1 時(shí)到達(dá)史密斯圓圖的圓周為止。具有|ρ|>1 的反射系數(shù)也可以在圖上表示出來。這種情況說明反射波大于入射波。這便為反射增益，當(dāng)存在負(fù)電阻時(shí)會(huì)出現(xiàn)這種情況。在球形史密斯圖上可以很靈巧地處理這種情況。圖10 顯示出了球形史密斯圖上|ρ|為常數(shù)時(shí)的曲線和ρ 的相位為常數(shù)時(shí)的曲線。緯線代表的是|ρ|為常數(shù)時(shí)的曲線，經(jīng)線代表的是當(dāng)ρ 的相位為常數(shù)時(shí)的曲線。北極點(diǎn)處于50Ω，反射系數(shù)為0（匹配完美的傳輸線），南極是-50Ω，反射系數(shù)為無窮大。赤道對應(yīng)的反射系數(shù)|ρ|=1。當(dāng)考慮反射系數(shù)時(shí)，北極和南極點(diǎn)對應(yīng)的阻抗有90°的相位差。

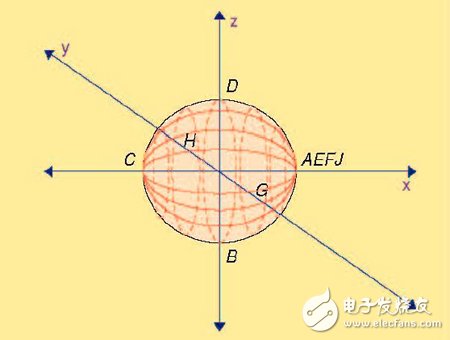
圖10、繪有常數(shù)|ρ|（|虛線）和常數(shù)反射相位（實(shí)線）的球形史密斯圓圖

圖形方式和計(jì)算機(jī)輔助設(shè)計(jì)

史密斯圓圖的擴(kuò)展涉及到將平面2-D的圓圖轉(zhuǎn)移到球面的3-D 圓圖上

史密斯圓圖的2-D 特征可以很容易地印在紙上或顯示在屏幕上。然而，對于3-D 史密斯圓圖來說，就并非如此了。要顯示史密斯圓圖以及在圖上畫出曲線和輪廓便會(huì)有些實(shí)際上的困難。一個(gè)辦法是做出打印好的小球。這會(huì)類似于一個(gè)塑料的足球，只不過代替六角形圖案的是電阻和感抗曲線。圖8 便是這樣一個(gè)例子。在過去的許多年里，我將其放在書桌上作為設(shè)計(jì)或直觀化的工具（我以前的一個(gè)同事為小球起名為Zelley 球，每次到我辦公室時(shí)都會(huì)向我仍這個(gè)球，并以此為樂）。也許，在每個(gè)本科微波授課的教室前的講臺上應(yīng)當(dāng)放一個(gè)這樣的球，類似于地理課上的地球儀。很明顯，在球上畫出仿真結(jié)果和輪廓會(huì)很費(fèi)事。同樣，手工在圖上劃線無法與常規(guī)計(jì)算機(jī)自動(dòng)設(shè)計(jì)流程一體化。

另一種方法是使用3-D 計(jì)算機(jī)軟件。這樣可以使得設(shè)計(jì)者能夠通過使用計(jì)算機(jī)鼠標(biāo)或鍵盤來旋轉(zhuǎn)和轉(zhuǎn)動(dòng)球形史密斯圓圖。有可能讓設(shè)計(jì)者選擇顯示阻抗，導(dǎo)納（或混合形式）的史密斯圓圖，將Q 或反射系數(shù)疊加在球的表面。球體是不透明的或半透明的。或許可以做多個(gè)球表面的2-D 投影，這可以成為計(jì)算機(jī)輔助設(shè)計(jì)的一個(gè)值得一試的折衷方案。

結(jié)論

本文重點(diǎn)討論了傳統(tǒng)2-D 史密斯圓圖的局限性。提出了一種克服這些局限的擴(kuò)展史密斯圓圖的想法。這種擴(kuò)展包括從2-D 阻抗平面轉(zhuǎn)換到三維，并將其映射到球體的表面。相信這是首次提出的史密斯圓圖的轉(zhuǎn)換方法。

然后考慮了球形史密斯圓圖的多種表示方法。包括使用常量電阻，電感，阻抗和反射系數(shù)曲線。最后，討論了如何用圖形方法來顯示3-D 史密斯圓圖。

需要指出的是，本文這里所討論的許多觀點(diǎn)還沒有進(jìn)行嚴(yán)密的數(shù)學(xué)運(yùn)算，所以有可能在球形的史密斯圓圖上出現(xiàn)一些不連續(xù)的地方。然而，基本的概念和想法是作者經(jīng)過了充分思考的，是完全能夠發(fā)表出來的。

希望本文所討論的3-D 史密斯圓圖可以在射頻和微波設(shè)計(jì)界或者用作設(shè)計(jì)工具，或者用于直觀化的幫助。希望本文至少提出了一個(gè)有趣的可供討論的課題。

致謝

作者Chris Zelley在此深深感謝Steve Cripps 和Gord Rabjohn 的幫助和建議，以及他們對作者構(gòu)思這篇文章所做的鼓勵(lì)。