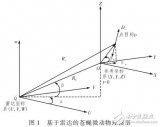
多普勒濾波器組

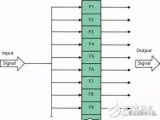
雷達是如何能夠同時檢測來自多個不同目標的回波，然后根據多普勒頻率的不同進行區別分類呢？從原理上來說是非常簡單的，即雷達接收的回波信號通過被稱為多普勒濾波器的一組數字濾波器來實現，如下圖所示。

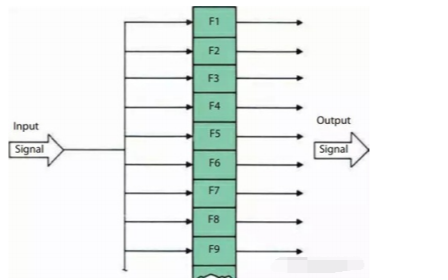
接收的雷達回波信號經過一組并行的濾波器后實現多普勒頻率分離。每個濾波器的設計都是為了得到一個較窄的多普勒頻帶，如圖所示。在理想情況下，只有每個濾波器在接收信號的頻率落在對應的頻帶內才會產生輸出；

而實際上由于濾波器旁瓣的原因，可能會在相鄰頻帶內出現信號泄露。如果按照距離/多普勒頻率進行排序，則在每個距離單元上進行獨立的多普勒濾波處理。

多普勒濾波器組的每個中心頻率點從低到高順序排列，為了使相鄰濾波器跨越目標頻率時的信噪比損失最小化，濾波器的通帶之間總會設計成相互交疊的形式，如圖所示。因此，在濾波器組相互交疊的區域都可能會有相鄰頻率信號的泄露。

在忽略濾波器旁瓣的條件下，每個濾波器只能夠通過某窄帶頻點的信號，當該信號的頻點離濾波器的中心頻率越近，輸出的信號幅度也越大。為了最小化濾波器輸出能量損失，當輸入信號頻率位于兩個相鄰濾波器之間時，采用相鄰濾波器通帶部分交疊的方法。

濾波器帶寬

窄帶濾波器的選擇特性也是在一段持續時間內表現出來的；能夠通過濾波器的頻帶寬度主要與信號的積累時間有關。

正弦信號（即脈沖波形）具有的頻譜波形，如圖所示。

濾波器帶寬與積累時間之間的關系與以前討論的方法有一些不同，即：

·保持濾波器調節系數為常數，按照一定的步進不斷改變輸入信號的頻率；

·濾波器積累時間控制在積累時間以內，確保信號持續時間至少為積累時間。

通過以上描述的方法，用圖形化的手段繪制出窄帶濾波器在不同頻率點的響應曲線。窄帶濾波器的中心主瓣區域是濾波器的通帶，主瓣區域的中心頻率為濾波器諧振頻率。如圖所示，濾波器頻譜的兩個過零點帶寬為2除以積累時間。

為了便于比較，將上圖在方位上的尺寸進行了調整，使得二者之間的零點寬度看起來是相同的。需要記住的是，積累時間通常為毫秒量級，而脈沖寬度大約為積累時間的千分之一，在微秒量級上。

如同天線輻射方向圖的主瓣一樣，濾波器的3dB帶寬（即輸出功率降低到最大值一半時的寬度）比零點到零點的帶寬更有用；與均勻輻射的天線相似，3dB帶寬大約是零點到零點帶寬的一半。即

為了達到以上帶寬，所應用的信號持續時間至少應當等于積累時間。在實際應用中，濾波器帶寬通常是基于最大可用的積累時間來確定的。

如果雷達輻射的波形是脈沖形式的，為達到給定信號帶寬就必須積累足夠的脈沖數量，由此可以看出，濾波器的3dB帶寬等于PRF除以積累脈沖數量。以上討論的帶寬是指最小可達到帶寬，根據實際工程應用，由于數字加權帶來的損失使得濾波器通帶會有所展寬。

濾波器組的通帶

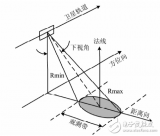
在整個帶寬內必須包括足夠多的濾波器來估計多普勒頻率的范圍，從而能夠覆蓋到預期設計的目標速度范圍。例如，預計最大的正多普勒頻率為100kHz，最大的負多普勒頻率為-30kHz，如下圖所示，則濾波器組的通帶范圍至少為100 + 30 = 130kHz，雷達工作重頻至少應大于130kHz。

當PRF大于最大與最小多普勒頻率所包括的范圍時，整個多普勒通帶應當設計得足夠寬以保證所有頻率分量能夠通過。

另一方面，如果PRF比期望的多普勒頻率擴展范圍小，則濾波器通帶的設計值應當小于PRF。這也用另一種方式證明了Nyquist定理，即任何信號的采樣頻率都必須達到信號最高頻率的兩倍來避免模糊。

如下圖所示，當PRF小于多普勒頻率的擴展寬度時，目標多普勒的旁瓣譜線會落在通帶以外，這時候只有目標多普勒的主瓣譜線能夠經過濾波后輸出。

當PRF小于多普勒頻率擴展范圍時，濾波器帶寬應當小于PRF，從而保證通帶內只有一個目標信號存在。

下圖描述了當濾波器通帶等于PRF或時目標譜線移動與濾波器組之間的關系，從圖中可以看出，在濾波器通帶內始終只落入了目標的一根主譜線；隨著目標多普勒頻率從低到高移動，相對應的諧波譜線也在不斷變化。

一般將通帶寬度設置為略小于，從而有效避免主瓣區域的地雜波，這樣能夠分離出靜止雜波和運動目標。在實際中為了簡化設計并不需要改變多普勒濾波器的頻率，而是將雷達回波的頻譜相對于濾波器組進行適當的搬移。