不知道你有沒有這種困惑,雖然刷了很多算法題,當我去面試的時候,面試官讓你手寫一個算法,可能你對此算法很熟悉,知道實現思路,但是總是不知道該在什么地方寫,而且很多邊界條件想不全面,一緊張,代碼寫的亂七八糟。如果遇到沒有做過的算法題,思路也不知道從何尋找,那么這篇文章就主要為你解決這幾個問題。
《劍指 offer》是準備數據結構與算法面試的一本好書,里邊很多面試手寫算法很多的注意的問題,但是基本都是用 C++ 實現的,書中每章節的分類都是按照性能和消耗以及手寫代碼的注意的幾大點進行了分類,針對每個不同的點,進行數據結構與算法的混合實現。
二遍刷題,發現了還可以根據自身情況進行整理和分類。全部代碼是用 JS 書寫,都經過 Leetcode 標準測試(小部分Leetcode 沒有的題目),對所有的算法題的特點進行總結分類,手寫算法中,如何考慮到全部的邊界條件;如果快速多種思路解決,如何將思路快速的轉化為代碼,這是這一篇重點分享的地方。
二叉樹題目共有 11 題,我把這 11 題書中對實現方法和思路有詳細的講解,但是對于個人來說,以后遇到陌生的二叉樹的題目怎么進行解決,通過對 11 個題的分析、整理,得出以下幾個步驟,首先先來看這 11 個二叉樹經典算法題。
PS:如果你已經做過這幾道題,而且能夠順利的手寫出來,不妨滑到最底部,希望最后的二叉樹思路、測試用例以及代碼編寫的總結對你在面試中有所幫助(這篇文章精華所在)。
No.1
面試題7:重建二叉樹
已知前序遍歷為{1,2,4,7,3,5,6,8},中序遍歷為{4,7,2,1,5,3,8,6},它的二叉樹是怎么樣的?
1、
思路
根據前、中序遍歷的特點,(根左右、左根右),先根據前序遍歷確定根節點,然后在中序遍歷知道該根節點的左右樹的數量,反推出前序遍歷中左子樹的結點有哪些。根據該思路進行遞歸即可完成二叉樹的重建。
2、
測試用例
完全二叉樹、非完全二叉樹 —— 普通測試。
只有左子節點二叉樹,只有右子節點、只有一個結點的二叉樹 —— 特殊二叉樹測試。
空樹、前序和中序不匹配 —— 輸入測試。
3、
代碼實現
1//定義結點 2//classTreeNode{ 3//constructor(data){ 4//this.data=data; 5//this.left=null; 6//this.right=null; 7//} 8//} 9 10//參數:前序遍歷數組~中序遍歷數組 11constreConstructBinaryTree=(pre,vin)=>{ 12//判斷前序數組和中序數組是否為空 13if(!pre||pre.length===0||!vin||vin.length===0){ 14return; 15} 16//新建二叉樹的根節點 17vartreeNode={ 18val:pre[0] 19} 20//查找中序遍歷中的根節點 21for(vari=0;i
No.2
面試題8:二叉樹的下一節點
給定一個二叉樹的節點,如何找出中序遍歷的下一節點。有兩個指向左右子樹的指針,還有一個指向父節點的指針。
1、
思路
求中序遍歷的下一節點,就要分各種情況(明確中序遍歷下一結點在二叉樹中的位置有哪些),然后對某種情況詳細分析。
下一結點可能存在的情況:
2、
測試用例
完全二叉樹、非完全二叉樹 —— 普通測試。
只有左子節點二叉樹,只有右子節點、只有一個結點的二叉樹 —— 特殊二叉樹測試。
空樹、前序和中序不匹配 —— 輸入測試。
3、
代碼實現
1constgetNextNode=(pNode)=>{ 2//判斷該結點是否為null 3if(pNode==null){ 4return; 5} 6 7//當前結點有右子樹且左子樹 8if(pNode.right!==null){ 9pNode=pNode.right; 10//判斷右子樹是否有左子樹 11while(pNode.left!==null){ 12pNode=pNode.left; 13} 14returnpNode; 15}else{ 16//判斷當前結點是否存在父節點(如果為空,沒有下一結點) 17while(pNode.next!==null){ 18if(pNode==pNode.next.left){ 19returnpNode.next; 20}else{ 21pNode=pNode.next; 22} 23} 24//沒有下一結點 25returnnull; 26} 27}
No.3
面試題26:樹的子結構
輸入兩棵二叉樹 A 和 B,判斷 B 是不是 A 的子結構。
1、
思路
通過判斷兩棵樹的根節點否相同,如果相同,則遞歸判斷樹剩余的結點是否相同。如果不相同,則遞歸樹的左右子節點進行對比找到相同的根節點。
2、
測試用例
是子結構、不是子結構 —— 普通測試。
只有左子節點、只有右子節點、只有一個結點 —— 特殊測試。
空樹 —— 輸入測試。
3、
代碼實現
1constTreeConstrutor=(nodeA,nodeB)=>{ 2constresult=false; 3//判斷輸入是否為null 4//nodeA為null不會有子結構 5if(nodeA==null){ 6returnfalse; 7} 8//如果nodeB為null,代表所有子結構比較完成 9if(nodeB==null){ 10returntrue; 11} 12 13//如果根節點相同,則進行子結構全部的驗證,返回驗證的結果 14if(nodeA.data===nodeB.data){ 15result=match(nodeA,nodeB) 16} 17 18//如果根節點不相同,繼續遞歸遍歷查找相同的根節點 19returnTreeConstrutor(nodeA.left,nodeB)||TreeConstrutor(nodeA.right,nodeB) 20} 21 22//匹配根節點相同的子結構 23constmatch=(nodeA,nodeB)=>{ 24if(nodeA==null){ 25returnfalse; 26} 27if(nodeB==null){ 28returntrue; 29} 30//判斷匹配的當前結點是否相同 31if(nodeA.data==nodeB.data){ 32//遞歸匹配其他子節點 33returnmatch(nodeA.left,nodeB.left)&&match(nodeA.right,nodeB.right); 34} 35 36//如果不相同 37returnfalse; 38}
No.4
面試題27:二叉樹的鏡像
請完成一個函數,如果一個二叉樹,該函數輸出它的鏡像。
1、
思路
根節點的左右子節點相互交換,繼續遞歸遍歷,將子節點的左右結點進行交換,知道遇到葉子節點。
2、
測試用例
完全二叉樹、非完全二叉樹 —— 普通測試。
只有左子節點二叉樹,只有右子節點、只有一個結點的二叉樹 —— 特殊二叉樹測試。
空樹 —— 輸入測試。
3、
代碼實現
1constinsert=(root)=>{ 2//判斷根節點是否為null 3if(root==null){ 4return; 5} 6 7//進行結點交換 8LettempNode=root.left; 9root.left=root.right; 10root.right=tempNode; 11 12//遞歸遍歷剩余的子節點 13insert(root.left); 14insert(root.right); 15 16//返回根節點 17returnroot; 18}
No.5
面試題28:對稱二叉樹
請實現一個函數,用來判斷一棵二叉樹是不是對稱的。如果一棵二叉樹和它的鏡像一樣,那么它是對稱的。
1、
思路
首先,觀察一個對稱的二叉樹有什么特點?
結構上:在結構上實對稱的,某一節點的左子節點和某一節點的右子節點對稱。
規律上:我們如果進行前序遍歷(根、左、右),然后對前序遍歷進行改進(根、右、左),如果是對稱的二叉樹,他們的遍歷結果是相同的。
考慮其他情況:
結點數量不對稱
結點值不對稱
2、
測試用例
對稱二叉樹、不對稱二叉樹(結點數量不對稱、結點結構不對稱)—— 普通測試。
所有結點值都相同的二叉樹 —— 特殊測試。
空二叉樹 —— 輸入測試。
3、
代碼實現
1varisSymmetric=(root)=>{ 2//判斷二叉樹是否為null——輸入測試,if(root==null){ 3returntrue; 4} 5 6//判斷輸入的二叉樹,從根節點開始判斷是否是對稱二叉樹 7varSymmetric=(lNode,rNode)=>{ 8//判斷左右結點是否都為null 9if(lNode==null&&rNode==null){ 10returntrue; 11} 12//判斷其中一個為null另一個不是null 13if(lNode==null&&rNode!==null){ 14returnfalse; 15} 16if(lNode!==null&&rNode==null){ 17returnfalse; 18} 19//判斷兩個結點的值是否相同 20if(lNode.val!==rNode.val){ 21returnfalse; 22} 23//如果相同,繼續遞歸判斷其他的結點 24returnSymmetric(lNode.left,rNode.right)&&Symmetric(lNode.right,rNode.left) 25} 26 27Symmetric(root.left,root.right) 28}
No.6
面試題32:從上到下打印二叉樹
從上到下打印出二叉樹的每個節點,同一層的節點按照從左到右的順序打印。(按層遍歷二叉樹)
1、
思路
從根節點開始按層遍歷打印結點(自左往右),下一層的遍歷是上一層的字節點,但是我們發現想要獲取到上層結點的子節點時,上層的父節點已經遍歷過去可,想要在獲取到,必須存儲父節點。然后下層遍歷的時候,自左往右取出父節點,依次打印子節點。
上方的解題思路中父節點的存儲和遍歷讓我們想到一個熟悉的數據結構,對了,“先進先出”的思想,那就是隊列。在遍歷上一層結點的時候,先打印結點值,然后判斷是夠存在左右子樹,如果存在,將給結點入隊,直到該層的結點全部遍歷完成。然后隊列出隊,分別打印結點,循環此步驟。
2、
測試用例
完全二叉樹、非完全二叉樹 —— 普通測試
只有左、右子節點的二叉樹、只有一個節點的二叉樹 —— 特殊測試
空樹 —— 輸入測試
3、
代碼實現
1、參數:樹的根節點。
2、判斷是否為空。
3、打印結點值,判斷該結點是否存在子節點,如果存在就入隊。
4、出隊,打印結點
5、循環上述步驟
1varlevelOrder=function(root){ 2letresult=[];//存放遍歷的結果 3//判斷根節點是否為null 4if(root==null){ 5return[]; 6} 7//聲明一個隊列 8letqueue=[]; 9queue.push(root) 10 11//出隊,打印結結點、判斷是否存在子節點 12while(queue.length!==0){ 13lettemp=[];//存儲每層的結點 14letlen=queue.length; 15for(letj=0;j
No.7
面試題33:二叉樹的后序遍歷序列
輸入一個整數數組,判斷該數組是不是某二叉搜索樹的后續遍歷。如果是返回 true,如果不是返回 false。假設輸入的任意兩個數字互不相同。
1、
思路
根據后續遍歷的規律和二叉樹具備的特點,可以找到的規律就是(左、右、根)序列的最后一個數為根節點,又根據二叉樹的特點,左子節點小于根節點,右子節點大于根節點,分離出左右子節點,根據上邊的規律,遞歸剩下的序列。
2、
測試用例
完全二叉樹、非完全二叉樹 —— 普通測試。
只有左子節點二叉樹,只有右子節點、只有一個結點的二叉樹 —— 特殊二叉樹測試。
空樹 —— 輸入測試。
3、
代碼實現
1、參數:數組
2、判斷數組是否為空
3、取數組的最后一個元素作為對比的根節點
4、根據根節點值的大小分割數組(分割數組的同時判斷是否都滿足小于根節點的要求)
5、判斷分割數組是否是空
6、遞歸上方的步驟
1constisPostorder=(arr)=>{ 2//判斷數組是否為null 3if(arr.length==0){ 4returntrue; 5} 6 7//取數組最后一個數字為根節點 8letrootVal=arr[arr.length-1]; 9 10//搜索小于根節點的值,并記錄該結點的下標(除根節點外) 11leti=0; 12for(;irootVal){ 14break 15} 16} 17 18//搜索大于根節點的值(除根節點外) 19letj=0; 20for(;jarr[j]){ 22returnfalse; 23} 24} 25 26//遞歸判斷左子節點的值(先判斷左子節點是夠有值),默認返回true 27letleft=true 28if(i>0){ 29left=isPostorder(arr.slice(0,i)) 30} 31//如果右子樹不為空,判斷右子樹為二叉搜索樹 32letright=true 33if(i
No.8
面試34:二叉樹和為某一值路徑
輸入一棵二叉樹和一個整數,打印出二叉樹中節點值的和為輸出整數的所有路徑。從樹的根節點開始往下一直到葉子節點所經過的節點形成一條路徑。
1、
思路
1、找規律:需要遍歷樹的所有結點:我們會想到前、中、后遍歷;需要存儲遍歷過的路徑(節點值):我們想到用數組存儲
2、算法思想:前序遍歷(根、左、右)的特點,從根到葉子節點,會從樹自左向右依次遍歷二叉樹,所有可能的路徑都會遍歷到,所以使用前序遍歷更佳。
每遍歷一個結點就將其累加,然后判斷累加的值是否等于目標值且子節點為葉子節點。如果是,則打印輸出該路徑;如果不是,則回退到上一父節點,此時數組中的數據結點進行刪除,然后不斷的遍歷下一子節點,遞歸。
3、綜上所述,存儲結點路徑的時候,涉及到累加結點和刪除節點,我們可以將其抽象成入棧和出棧。然后遍歷二叉樹的所有路徑可以用到遞歸的過程,讓出棧和入棧與遞歸的狀態達成一致,這到題就不難了。
2、
測試用例
完全二叉樹、非完全二叉樹(有一條路徑滿足、有多條路徑滿足、都不滿足)—— 普通測試。
只有左子節點的二叉樹、只有右子節點的二叉樹、只有一個結點的二叉樹 —— 特殊測試。
空二叉樹、輸入負數 —— 輸入測試。
3、
代碼實現
1consttreeSum=(root,targetSum)=>{ 2//判斷輸入的二叉樹和整數 3if(root==null||targetSum{ 20//將當前跟根節點進行累加 21currentSum=currentSum+root.val; 22 23//存儲棧中 24pathStack.push(root.val); 25 26//判斷目標值是否相等且是否為葉子節點 27if(currentSum==targetSum&&root.left==null&&root.right==null){ 28//打印路徑 29result.push(pathStack.slice(0)) 30} 31 32//如果左子節點不為空 33if(root.left!==null){ 34FindPath(root.left,targetSum,currentSum,pathStack,result); 35} 36 37//如果當前結點還有右子樹,繼續遍歷 38if(root.right!==null){ 39FindPath(root.right,targetSum,currentSum,pathStack,result); 40} 41 42//該路徑遍歷到葉子節點,還沒有滿足條件,則退回到父節點,進行下一結點的累加判斷 43pathStack.pop(); 44}
No.9
面試題37:序列化二叉樹
請實現兩個函數,分別用來序列化二叉樹和反序列化二叉樹。
1、
思路
1、序列化:遍歷二叉樹,遇到葉子節點,將其轉化為 $ 表示。
2、反序列化:根據前序遍歷的特點(根、左、右),進行二叉樹的還原。
2、
測試用例
完全二叉樹、非完全二叉樹 —— 普通測試。
只有左子節點二叉樹,只有右子節點、只有一個結點的二叉樹 —— 特殊二叉樹測試。
空樹 —— 輸入測試。
3、
代碼實現
1letresult=[]; 2varserialize=function(root){ 3//判空 4if(root==null){ 5result.push('$'); 6return; 7} 8//前序遍歷 9result.push(root.val) 10serialize(root.left) 11serialize(root.right) 12//打印 13console.log(result) 14}; 15 16serialize(symmetricalTree);
No.10
面試題54:二叉樹的第 K 大節點
給定一棵二叉搜索樹,請找出其中的第 K 大節點。
1、
思路
要想找到第 K 大結點必要要知道排序,二叉樹的前、中、后遍歷中的中序遍歷就是從小到大排序。然后遍歷的同時計數找到第 K 大節點。
2、
測試用例
完全二叉樹、非完全二叉樹 —— 普通測試。
只有左子節點的二叉樹、只有右子節點的二叉樹、只有一個節點的二叉樹 —— 特殊測試。
K 的范圍、空樹 —— 輸入測試。
3、
代碼實現
1//求二叉樹中第K大節點 2varkthTallest=function(root,k){ 3letres=[] 4//遍歷 5constinorder=(root)=>{ 6if(root){ 7inorder(root.left); 8res.push(root.val); 9inorder(root.right); 10} 11} 12//調用 13inorder(root); 14returnres[res.length-k] 15};
No.11
面試題55:二叉樹的深度
輸入一棵二叉樹的根節點,求該樹的深度。從根節點到葉子節點依次經過的節點(包含根、葉子節點)形成樹的一條路徑,最長路徑的長度樹的深度。
1、
思路
思路一:按層遍歷,對按層遍歷的算法進行改進,每遍歷一次層進行加一。
思路二:尋找最長路徑,借助遍歷最長路徑的設計思路記性改進。只需記錄兩個子樹最深的結點為主。
2、
測試用例
完全二叉樹、非完全二叉樹 —— 普通測試。
只有左子節點二叉樹,只有右子節點、只有一個結點的二叉樹 —— 特殊二叉樹測試。
空樹、前序和中序不匹配 —— 輸入測試。
3、
代碼實現
1varmaxDepth=function(root){ 2//如果根節點為null 3if(root===null)return0; 4 5//遞歸左子樹 6letdepthLeft=maxDepth(root.left); 7 8//遞歸右子樹 9letdepthRight=maxDepth(root.right); 10 11//將子問題合并求總問題 12returnMath.max(depthLeft,depthRight)+1; 13};
總結歸納
通過《劍指 offer》以上十一個題,不是做過之后就記住了這么簡單,而是通過以上二叉樹題型的總結歸納,能不能舉一反三,總結出二叉樹面試題的解題思路,以后遇到二叉樹相面試題能不能通過上邊總結出來的步驟進行思考獨立解決,這是這篇文章的重點。下面就分別通過解題思路、測試用例以及編寫代碼進行深入總結。
解題思路總結
1、根據樹前(根左右)、中(左根右)、后(左右根)序遍歷的規律來解決問題。
通過二叉樹的遍歷來找到規律,從而找到解題思路。
重建二叉樹
根據前、中序遍歷,找到二叉樹的根節點和左右子樹的規律,然后遞歸構建二叉樹。
二叉樹的下一節點
根據中序遍歷,找出包含任何節點的一下節點的所有可能情況,然后根據情況分別進行判斷。
二叉樹的后續遍歷序列
通過中序遍歷找到打印二叉樹結點的規律,可以判斷此后續遍歷是否為二叉樹。
二叉樹和為某一值的路徑
選擇二叉樹的遍歷,對每個節點進行存儲判斷,然后根據二叉樹葉子節點的特點,進行對問題的解決。
二叉樹的第 K 大結點
中序遍歷的結果是從小到大,然后倒數找到第 K 大數據。
序列化二叉樹
遍歷二叉樹,遇到 null 轉化為特殊符號。
2、根據樹的結構尋找規律來解決問題
通過二叉樹的特點:左子節點小于父節點、右子節點大于父節點、樹的節點可以進行遞歸等,以上特點又是更好的幫我們解決思路。
樹的子結構
根據子結構和主體樹的特點,對其樹的結構進行分析,可以找到解題的思路。
鏡像二叉樹
觀察鏡像二叉樹的左右子節點交換特點,可以找到解題思路。
對稱二叉樹
觀察對稱二叉樹有什么特點,在結構上和遍歷上尋找特點和規律,可以找到解題思路。
按層遍歷二叉樹
根據二叉樹每層節點的結構關系(父子關系),可以進行每層遍歷,通過上層找到下層的遍歷結點。
反序列化二叉樹
根據遍歷的規律和二叉樹的規律,將遍歷結果生成一棵二叉樹。
測試用例總結
通過以上題目中,我將測試用例分為三大種,測試代碼的時候,在這三大種進行想就可以了。
※普通測試
※特殊測試
※輸入測試
1
普通測試
普通測試從兩個方面去想,第一個方面就是問題的本身,比如對稱二叉樹的判斷,普通測試就是分別輸入一個對稱二叉樹和非對稱二叉樹進行測試。第二個方面就是問題本身沒有什么可以找到的測試,比如按層遍歷二叉樹,它的普通測試就是分別輸入完全二叉樹(普通二叉樹也可以),非完全二叉樹進行測試。
2
特殊測試
特殊測試強調的是樹的特殊性,特殊的二叉樹就那么幾個,比如:只有左子節點的二叉樹、只有右子節點的二叉樹、只有一個節點的二叉樹、沒有結點的二叉樹。
3
輸入測試
輸入測試,顧名思義,要對用戶輸入的參數進行判斷,比如,你輸入一棵樹,要判斷是否為空。再比如,求最大 K 結點,對 K 的取值范圍進行判斷。
代碼編寫
將二叉樹的解題思路轉化為代碼除了熟練最基本的二叉樹的增、刪、改、查之外,最重要的就是二叉樹的遞歸,因為二叉樹的結構決定了用遞歸解決二叉樹問題更加簡便。但是遞歸的書寫并不僅簡單,因為它有遞和歸的過程,大腦并不能更好的去處理這些,可以去看之前總結遞歸的文章《數據結構與算法之遞歸系列》。
書寫二叉樹遞歸問題有一點特別重要,不要嘗試的去想那個遞歸的過程,而是先去尋找到遞歸的終止條件,然后對每次遞歸的結果進行判斷,然后讓他遞歸去吧,再次強調千萬別去思考過程。
學習編程不是做了多少題,而是能不能在做過的題和項目中總結經驗,這是快速成長的必要條件。非常感謝各位的大力支持,下一篇我們再見。
-
代碼
+關注
關注
30文章
4670瀏覽量
67764 -
二叉樹
+關注
關注
0文章
74瀏覽量
12283
原文標題:面試二叉樹看這 11 個就夠了
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
原理圖設計里兩顆重要的樹(國產EDA)
哈夫曼編碼怎么算 哈夫曼編碼左邊是0還是1
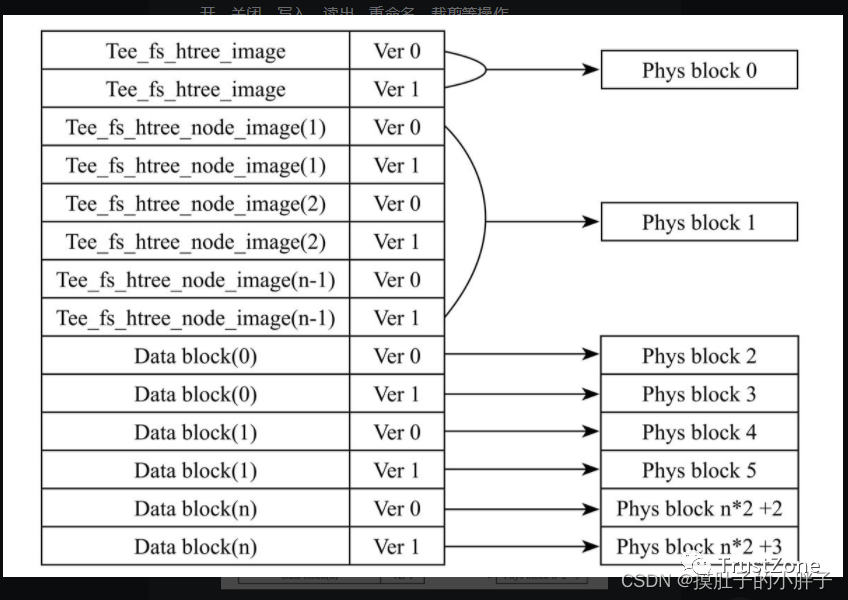
OP-TEE安全存儲安全文件的格式
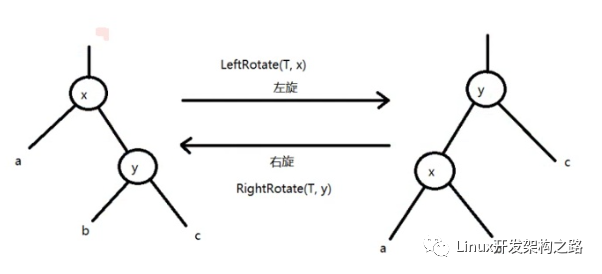
紅黑樹的特點及應用
為什么MySQL索引要用B+tree?
數據結構面試之二叉樹相關操作




 面試二叉樹看這11個就夠了
面試二叉樹看這11個就夠了










評論