1、 數字濾波分析
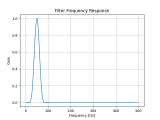
根據數字濾波的原理,數字圖像經過數字卷積濾波處理,可以達到削減噪聲信號、增強邊界清晰度、提取某方向的信息等特殊效果。下圖顯示數字卷積濾波的過程。
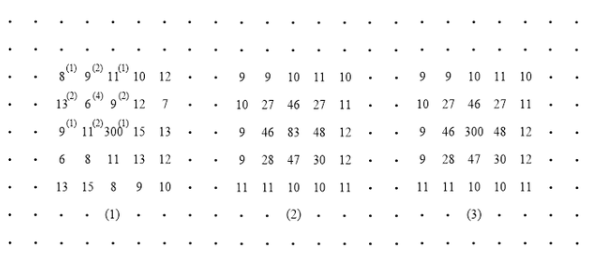
數字卷積濾波過程示意圖
上圖為一數字圖像的部分數據,每個數字表示像素的灰度值,其中的部分數據和周圍數據差異很大。其中帶括號的數字共同組成了卷積濾波模板,它是一個奇數行奇數列的數字陣列,陣列中心成為卷積核心。
卷積濾波過程就是將卷積核心分別對應要處理的數值,卷積濾波模板的其它參數對應要處理數值周圍的數值,把卷積濾波模板對應范圍內的數值分別和卷積濾波模板內的參數相乘,然后再求這些乘積的代數和,最后除以卷積濾波模板的系數(卷積濾波模板內各參數的代數和),得到了處理后的數值,將此數值代替數字圖像中卷積核心對應的數值,然后將卷積濾波模板移動一個像元,重復以上的計算,直到數字圖像的每個像元都被處理完為止,處理后的部分數據如下圖所示。觀察處理的數據可以發現,異常數據對周圍數據的影響體現得比較明顯。用卷積濾波模板處理完數據以后,再把異常數據再重新賦值回去,這樣既體現了異常點對周圍數據的影響,又不改變它自身的既定數值。
將以上計算過程表達成一般的計算公式,可寫作:

2、 分形理論
分形理論是研究復雜體系的新方法,它的核心思想是將一個存在某種精細結構自相似的隨機復雜幾何體,描述成有限階分形的組合。
本著對復雜曲面分形描述,逐階逼近的原則,我們可以將研究區域中所有樣本點屬性數據算術平均,該算術平均作為零階分形的屬性值,記做MDG[F0(0,0)],當然這僅是研究區域最為粗略的描述。將研究區域分為m×n的子區域,通常每個子區域都包含著若干個樣本點,逐個地對每個子區域內的樣本點屬性值取其算術平均,子區域中樣本點屬性平均值記做MDS[F1(i,j)],F1(i,j)表示第i行(i=0,1,2),第j列(j=0,1,2)的第一階分形子區域。考慮到本階分形子區域是上階分形子區域的局部,因為本階分形子區域屬性賦值要受到上階分形子區域的影響。我們用加權平均解決,既:
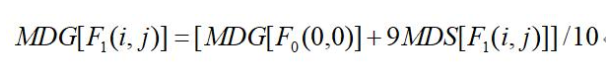
注意本階分形子區域樣本點屬性平均值的權重我們取9,而上階分形子區域的權重取1,突出當前階分形子區域樣本點屬性平均值的作用。當然,這兩個權重值是可以調整的。這樣每個分形子區域(1階分形就有91=9個子區域)都賦有屬性值。重復上面的做法,直到分形子區域的大小達到要求的網格大小為止。
-
數字濾波
+關注
關注
1文章
56瀏覽量
16842 -
分形理論
+關注
關注
0文章
6瀏覽量
6669
發布評論請先 登錄
相關推薦
ADC3663數字濾波器如何使用呢?
基于FPGA實現FIR數字濾波器
用DM642做音頻的數字濾波時總是有很大的雜聲,怎么解決?
濾波參數tor對數字濾波結果的影響
數字濾波器的實現方法
數字濾波器的原理和應用
數字濾波器是如何工作的




 數字濾波和分形理論的分析和原理
數字濾波和分形理論的分析和原理











評論