問題描述：

在一塊電路板的上、下兩端分別有n個接線柱。根據電路設計，要求用導線（i，π（i）） 將上端接線柱i與下端接線柱π（i）相連，如下圖。其中，π（i），1≤ i 《≤n，是｛1，2，…，n｝的一個排列。導線（I， π（i））稱為該電路板上的第i條連線。對于任何1 ≤ i ≤ j ≤n，第i條連線和第j條連線相交的充要條件是π（i）》 π（j）。

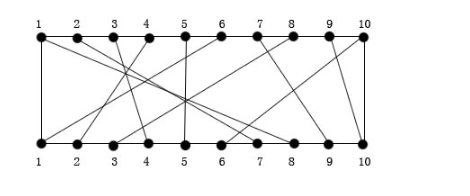
在制作電路板時，要求將這n條線分布到若干個絕緣層上，在同一層上的連線不能相交。電路布線問題要確定將哪些連線安排在第一層上，使得該層上有盡可能多的連線。換句話說，該問題要求確定導線集Nets = ｛i，π（i），1 ≤ i ≤ n｝的最大不想交子集。

問題分析：

1. 最優子結構性質

記N（i，j） = {t|（t， π（i）） ∈ Nets，t ≤ i， π（t） ≤ j }。 N（i，j）的最大不相交子集為MNS（i，j）。Size（i，j）=|MNS（i，j）|。

1） 當i = 1時

2） 當i 》1時，

① j 《π（i）。此時，（i，π（i）） 不屬于N（i，j）。故在這種情況下，N（i，j） = N（i-1，j），從而Size（i，j）=Size（i-1，j）。

② j ≥π（i）。此時，若（i， π（i））∈MNS（i，j），則對任意（t， π（i））∈MNS（i，j）有t 《 i且π（t）《 π（i）；否則，（t，π（t））與（i， π（i））相交。在這種情況下MNS（i，j）-{（i， π（i））}是N（i-1， π（i）-1）的最大不相交子集。否則，子集MNS（i-1，π（i）-1）∪{（i， π（i））}包含于N（i，j）是比MNS（i，j）更大的N（i，j）的不相交子集。這與MNS（i，j）的定義相矛盾。

若（i， π（i））不屬于MNS（i，j），則對任意（t， π（t））∈MNS（i，j），有t《i。從而MNS（i，j）包含于N（i-1，j），因此，Size（i，j）≤Size（i-1，j）。

另一方面，MNS（i-1，j）包含于N（i，j），故又有Size（i，j） ≥Size（i-1，j），從而Size（i，j）= Size（i-1，j）。

2. 遞歸計算最優值

經以上后分，可電路布線問題的最優值為Size（n，n）。由該問題的最優子結構性質可知：

C++程序：

//CircuitLayout.h

#ifndef CIRCUITLAYOUT_H

#define CIRCUITLAYOUT_H

class CircuitLayout{

private：

int count;//最大連線柱

int *c;//int **Size;//最大連線數目

int *net;//存儲連線

bool Input（）;

int max（int，int）;

void mnset（int *c，int **Size）;//計算最優值

int traceback（int *c，int **Size，int *net）;//構造最優解

public：

CircuitLayout（）;

~CircuitLayout（）;

bool Run（）;//運行接口函數

};

#endif

//CircuitLayout.cpp

#include “CircuitLayout.h”

#include 《iostream》

#include 《math.h》

using namespace std;

#define MAX（a，b） （（（a）》（b）？（a）：（b）））

#define M 50

CircuitLayout：：CircuitLayout（）{

int N = 0;

c = new int［M］;

net = new int［M］;

Size = new int*［M］;

for（int i=0;i《M;++i）

Size［i］ = new int［M］;

}

CircuitLayout：：~CircuitLayout（）{

for（int i=0;i《M;++i）

delete ［］Size［i］;

delete ［］Size;

delete ［］c;

delete ［］net;

}

bool CircuitLayout：：Input（）{

int n;

cout 《《 “請輸入接線柱的個數： ”;

cin 》》 n;

count = n;

cout 《《 “請依次輸入被連接數： ” 《《 endl;

for（int i=0;i《n;++i）

cin 》》 c［i］;

if（c） return true;

else return false;

}

int CircuitLayout：：max（int a，int b）{

if（a 》= b） return a;else return b;

}

void CircuitLayout：：mnset（int *c，int **Size）{

int i=0;

int j=0;

int n = count-1;

for（j=0;j《c［1］;j++）

Size［1］［j］ = 0;

for（j=c［1］;j《=n;j++）

Size［1］［j］ = 1;

for （i=2;i《n;i++）{

for （j=0; j《c［i］ ; j++）

Size［i］［j］ = Size［i-1］［j］;

for （j=c［i］;j《=n;j++）

Size［i］［j］ = max（Size［i-1］［j］，Size［i-1］［c［i］-1］+1）;

}

Size［n］［n］ = max（Size［n-1］［n］，Size［n-1］［c［n］-1］+1）;

cout 《《 “s［n］［n］： ” 《《 Size［n］［n］ 《《 endl;

}

int CircuitLayout：：traceback（int *c，int **Size，int *net）{

int n = count-1;

int j = n;

int m = 0;

for （int i=n;i》0;i--）{

if （Size［i］［j］ ！= Size［i-1］［j］）{

net［m++］ = i; j = c［i］ - 1;

}

}

if（j》=c［0］）

net［m++］ = 0;

for（int k=0;k《m;++k）

cout 《《 “net： ” 《《 net［k］ 《《 “ ”;

cout 《《 endl;

return m;

}

bool CircuitLayout：：Run（）{

int msize = 0;

if（Input（））{

mnset（c，Size）;

msize = traceback（c，Size，net）;

cout 《《 “msize： ”《《 msize;

cout 《《 endl;return true;

}

else return false;}

int main（）{

CircuitLayout xiaoli;

xiaoli.Run（）;

return 0;

}