《算法設計與分析》 --王曉東
題目描述:
在一塊電路板的上、下2端分別有n個接線柱。根據電路設計,要求用導線(i,a(i))將上端接線柱與下端接線柱相連,其中a(i)表示上端點i對應的向端點的值。如圖所示:
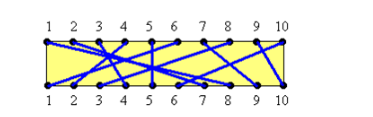
題目要求是在給定的連線中,選取不相交連線的最大子集,即不相交連線的最大數目。并把最大不相交子集的情況給列舉處理啊。
解題思路:
首先用a[i]數組表示與上面對應點相連線的下面的點,再用set[i][j]表示上面節點i與下面節點j連線的左邊(包括i j連線)的最大不相交連線的個數。
于是就有公式:
max(set[i-1][j], set[i][j-1]); j != a[i]
set(i,j) =
set[i-1][j-1] + 1; j == a[i]
然后就可以對每一個i,都對所以的j求一遍。這樣就可以得出結果嗎,set[n][n]即我們想要的結果。
最后通過回溯把結果輸出出來。
代碼實現:
#include 《stdio.h》
#define MAX(a,b) ((a) 》 (b) ? (a) : (b))
void circut(int a[],int set[][11],int n);
void back_track(int i,int j,int set[][11]);
int main()
{
int a[] = {0,8,7,4,2,5,1,9,3,10,6};
int set[11][11];
circut(a,set,10);
printf(“max set: %d \n”,set[10][10]);
back_track(10,10,set);
printf(“\n”);
return 0;
}
void circut(int a[],int set[][11],int n)
{
int i,j;
for (i = 0; i 《 n; i++)
{
set[i][0] = 0;
set[0][i] = 0;
}
for (i = 1; i 《= n; i++)
{
for (j = 1; j 《= n; j++)
{
if (a[i] != j)
set[i][j] = MAX(set[i-1][j],set[i][j-1]);
else
set[i][j] = set[i-1][j-1] + 1;
}
}
}
void back_track(int i,int j,int set[][11])
{
if (i == 0)
return;
if (set[i][j] == set[i-1][j])
back_track(i-1,j,set);
else if (set[i][j] == set[i][j-1])
back_track(i,j-1,set);
else
{
back_track(i-1,j-1,set);
printf(“(%d,%d) ”,i,j);
}
}
-
電路板
+關注
關注
140文章
4907瀏覽量
97426 -
數組
+關注
關注
1文章
415瀏覽量
25910
發布評論請先 登錄
相關推薦
電路設計寶典:淺談555電路設計
FPGA布線開關的電路設計
高頻電路設計布線技巧
高頻電路設計布線技巧概述!
講解高速PCB的布線、布局和電路設計

如何解決高頻電路的布線





 淺談電路布線電路設計
淺談電路布線電路設計










評論