前言 接觸深度學習也有一兩年了，一直沒有將一些實戰經驗整理一下形成文字。本文打算用來記錄一些在深度學習實踐中的調試過程，記錄一些經驗之談。因為目前深度學習業界的理論基礎尚且薄弱，很多工程實踐中的問題沒法用理論解釋得很好，這里的只是實踐中的一些經驗之談，以供參考以及排錯。本文將持續更新。 需要強調的是，本文的很多單純只是經驗，在盡可能列出參考文獻的同時卻并無嚴格理論驗證，希望大家見諒。歡迎大家集思廣益，共同維護這個經驗集，為整個社區貢獻微弱力量。

1、在分類問題中，損失函數及其快速得下降為0.0000 在分類問題中，我們一般采用的是交叉熵[1]作為損失函數，如式(1.1)所示 其中和是預測結果，以概率分布的形式表達，如等，一般是通過softmax層實現，和是樣本真實標簽，在單分類問題中，采用的是獨熱編碼[2]，只有一個分量是為1的，如。（公式第二行是向量化表達）我們發現，交叉熵損失的下確界是0，但是永遠都不可能達到0，因為要達到0，那么所有的預測向量分布就必須完全和真實標簽一致，退化為獨熱編碼。但是實際上在神經網絡中，經過了softmax層之后，是不可能使得除了目標分量的其他所有分量為0的（這個這里只是拋出了結論，討論需要比較長的篇幅。），因此永遠不可能達到0的，正是因為如此，交叉熵損失可以一直優化，這也是其比MSE損失優的一個點之一。 既然注意到了不可能為0，我們就可以分析，這肯定是自己程序問題，我們將經過softmax之前的logit打印出，如： 發現了沒有，這些值都很大，而softmax函數為: 我們會發現，過大或者過小的指數項，比如1023，會涉及到計算，這個數值在TensorFlow或者大部分框架中是溢出的，顯示為inf，因此就會把該分量拉成1，而其他變成了0。這種操作是會導致嚴重的過擬合的。因此，一般來說，logit值不能太大，否則將會出現數值計算問題。 那么如何解決？出現這種問題的情況很多時候是因為參數初始化導致的數值計算問題，比如都采用了方差過小的高斯分布進行初始化，那么就會把網絡的輸出的范圍拉的特別大，導致以上的問題。因此在參數初始化中，確保每一層的初始化都是在一定范圍內的，可以考慮采用Xavier初始化，Kaiming初始化等。（這個初始化的影響我們將會以后討論，這是一個新的話題。）
2、在正則化的過程中對神經網絡的偏置也進行了正則 一般來說，我們常用的是二范數正則，也即是嶺回歸，如式子(2.1) 一般來說，我們只會對神經網絡的權值進行正則操作，使得權值具有一定的稀疏性[21]或者控制其尺寸，使得其不至于幅度太大[3]，減少模型的容量以減少過擬合的風險。同時，我們注意到神經網絡中每一層的權值的作用是調節每一層超平面的方向（因為就是其法向量），因此只要比例一致，不會影響超平面的形狀的。但是，我們必須注意到，每一層中的偏置是調節每一層超平面的平移長度的，如果你對偏置進行了正則，那么我們的可能就會變得很小，或者很稀疏，這樣就導致你的每一層的超平面只能局限于很小的一個范圍內，使得模型的容量大大減少，一般會導致欠擬合[7]的現象。 因此，一般我們不會對偏置進行正則的，注意了。
3、學習率太大導致不收斂 不收斂是個范圍很大的問題，有很多可能性，其中有一種是和網絡結構無關的原因，就是學習率設置的太大了，如下圖所示，太大的學習率將會導致嚴重的抖動，使得無法收斂，甚至在某些情況下可能使得損失變得越來越大直到無窮。這個時候請調整你的學習率，嘗試是否可以收斂。當然，這里的“太大”目前沒有理論可以衡量，不過我喜歡從的Adam優化器[4]開始進行嘗試優化。

下圖展示了過大過小的學習率對模型性能的影響曲線圖：

4、別在softmax層前面的輸入施加了激活函數 softmax函數如式(4.1)所示： 假設我們的網絡提取出來的最后的特征向量是，如果我們最后的分類的類別有類，那么我們會用一個全連接層將其映射到對應維度的空間里面，如式(4.2)。 那么，這個全連接層雖然說可以看成是分類器，但是我們最好把它看成是上一層的“近線性可分特征”的一個維度轉換（有點繞，意思是我們這里只是一個維度的轉換，而不涉及到kernel），不管怎么說，這個時候，我們的輸出是不能有激活函數的，如下式是不可以的： 這時候的輸出，具有和分類類別相同的維度，在很多框架中被稱之為logits值，這個值一般是在實數范圍內的，一般不會太大，參考筆記第一點的情況。
5、檢查原數據輸入的值范圍 原始數據輸入可能千奇百怪，每個特征維的值范圍可能有著數量級上的差別，這個時候如果我們不對數據進行預處理，將會大大增大設計網絡的負擔。一般來說我們希望輸入的數據是中心對齊的，也即是0均值的[5]，可以加速網絡收斂的速度。同時，我們希望不同維度上的數值范圍是一致的，可以采用一些歸一化[6]的手段進行處理（這個時候假設每個維度重要性是一樣的，比如我們圖片的三個通道等）。
6、別忘了對你的訓練數據進行打亂 經常，你的訓練過程非常完美，能夠很好地擬合訓練數據，但是在測試過程中確實一塌糊涂，是的，你的模型這個時候過擬合[7]了。這個時候你會檢查模型的有效性，不過在進行這一步之前，不妨先檢查下你的數據加載器(Data Loader)是否是正常設計的。 一般來說，我們的訓練數據在訓練過程中，每一個epoch[8]中，都是需要進行打亂(shuffle)的，很多框架的數據加載器參數列表中都會有這項選項，比如pytorch的DataLoader類[9]。為什么需要打亂呢？那是因為如果不打亂我們的訓練數據，我們的模型就有可能學習到訓練數據的個體與個體之間特定的排列順序，而這種排列順序，在很多情況下是無用的，會導致過擬合的糟糕現象。因此，我們在訓練過程中，在每一個epoch訓練中都對訓練集進行打亂，以確保模型不能“記憶”樣本之間的特定排序。這其實也是正則的一種手段。 在訓練中，大概如：
7、一個batch中，label不要全部相同 這個情況有點類似與筆記的第六點，我們需要盡量給訓練過程中人為引入不確定性，這是很多正則手段，包括dropout，stochastic depth等的思路，這樣能夠有效地減少過擬合的風險。因此，一個batch中，盡量確保你的樣本是來自于各個類的（針對分類問題而言），這樣你的模型會減少執著與某個類別的概率，減少過擬合風險，同時也會加快收斂速度。
8、少用vanilla SGD優化器 在高維度情況下的優化，其優化平面會出現很多鞍點（既是梯度為0，但卻不是極點），通常，鞍點會比局部極值更容易出現（直觀感受就是，因為高維度情況下，一個點周圍有很多維度，如果是極值點，那么就需要其他所有維度都是朝向同一個方向“彎曲”的，而這個要比鞍點的各個方向“彎曲”的情況可能要小），因此這個時候我們更擔心陷于鞍點，而不是局部極小值點（當然局部極小值點也是一個大麻煩，不過鞍點更麻煩）。如果采用普通的SGD優化器，那么就會陷于任何一個梯度為0的點，也就是說，極有可能會陷于鞍點。如果要使用SGD方法，建議使用帶有momentum的SGD方法，可以有效避免陷入鞍點的風險。

下圖是某個函數的三維曲線圖和等高線圖，我們可以看到有若干個局部最優點和鞍點，這些點對于vanilla SGD來說是不容易處理的。

9、檢查各層梯度，對梯度爆炸進行截斷 有些時候，你會發現在訓練過程中，你的損失突然變得特別大，或者特別小，這個時候不妨檢查下每一層的梯度（用tensorboard的distribution可以很好地檢查），很可能是發生了梯度爆炸(gradient explosion)的情況，特別是在存在LSTM等時序的網絡中，很容易出現這種情況。因此，這個時候我們會用梯度截斷進行處理，操作很簡單粗暴，就是設置一個閾值，把超過這個閾值的梯度全部拉到這個閾值，如下圖所示：

在tensorflow中也提供了相應的API供梯度截斷使用[10]，如：

tf.clip_by_value( t, clip_value_min, # 指定截斷最小值 clip_value_max, # 指定截斷最大值 name=None) 具體使用見[11]，在應用梯度之前，對梯度截斷進行處理。 10、檢查你的樣本label 有些時候，你的訓練過程可以很好地收斂，當使用MSE損失[12]的時候甚至可能達到0.0000的情況。但是，當你把模型拿到測試集中評估的時候，卻發現性能極差，仿佛沒有訓練一樣。這是過擬合嗎？顯然是的，但是這可能并不是你的模型的問題，請檢查你的數據加載中訓練集的樣本標簽是否正確對應。 這個問題很白癡，但是卻真的很容易在數據加載過程中因為種種原因把label信息和對應樣本給混掉。根據文獻[13]中的實驗，用MSE損失的情況下，就算是你的label完全隨機的，和樣本一點關系都沒有，也可以通過基于SGD的優化算法達到0.0000損失的。因此，請務必確保你的樣本label是正確的。 11、分類問題中的分類置信度問題 在分類問題中我們一般都是采用的是交叉熵損失，如式子(1.1)所示，在一些實驗中，如果我們繪制出訓練損失和分類準確度的曲線圖，我們可能會有下圖這種情況[14]：

其中上圖為分類損失，紫色為訓練損失，藍色為測試損失，下圖為分類準確度，綠色為訓練準確度，藍色為測試準確度。我們不難發現一個比較有意思的現象，就是當測試損失開始到最低點，開始向上反彈的時候，其測試準確度卻還是上升的，而不是下降。這是為什么呢？為什么分類準確度不會順著分類損失的增大而減少呢？ 這個涉及到了分類過程中對某個類的“置信程度”的多少，比如： 模型是對第一類相當確信的，但是在第二種情況： 這對第一類的置信程度就很低了，雖然按照貝葉斯決策，還是會選擇第一類作為決策結果。因此這就是導致以上現象的原因，在那個拐點后面，這個模型對于分類的置信程度其實已經變得很差了，雖然對于準確度而言，其還能分類正確。但是這其實正是過擬合的一種表現，模型已經對自己的分類結果不確信了。 12、少在太小的批次中使用BatchNorm層 Batch Normalization[15]，中文譯作批規范化，在深度學習中是一種加快收斂速度，提高性能的一個利器，其本質和我們對輸入的原數據進行0均值單位方差規范化差不多，是以batch為單位，對中間層的輸出進行規范化，可以緩和內部協方差偏移(Internal Covariate Shift)的現象。其基本公式很簡單，如下： 不過這里并不打算對BN進行詳細講解，只是想告訴大家，因為BN操作在訓練過程中是對每個batch進行處理的，從每個batch中求得均值和方差才能進行操作。如果你的batch特別小（比如是受限于硬件條件或者網絡要求小batch），那么BN層的batch均值和方差可能就會不能很好符合整個訓練集的統計特征，導致差的性能。實際上，實驗[16]說明了這個關系，當batch小于16時，性能大幅度下降。

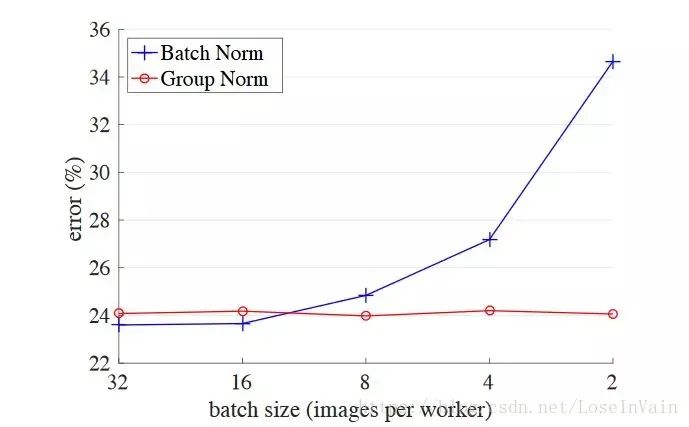
因此，少在太小的batch中使用BN層，如果實在要使用，在發生性能問題時優先檢查BN層。 13、數值計算問題，出現Nan Nan(Not An Number)是一個在數值計算中容易出現的問題，在深度學習中因為涉及到很多損失函數，有些損失函數的定義域并不是整個實數，比如常用的對數，因此一不小心就會出現Nan。在深度學習中，如果某一層出現了Nan，那么是具有傳遞性的，后面的層也會出現Nan，因此可以通過二分法對此進行排錯。 一般來說，在深度學習中出現Nan是由于除0異常或者是因為損失函數中的（比如交叉熵，KL散度）對數操作中，輸入小于或者等于0了，一般等于0的情況比較多，因此通常會： 這里的是個很小的值，一般取即可，可以防止因為對數操作中輸入0導致的Nan異常。 需要注意的是，有些時候因為參數初始化或者學習率太大也會導致數值計算溢出，這也是會出現Nan的，一般這樣會出現在較前面的層里面。 14、BN層放置的位置問題 BN層有兩種常見的放置位置，如下圖所示：第一個是放在激活函數之前：

第二個是放在激活函數之后：

在原始BN的論文[15]中，Batch Norm(BN)層是位于激活層之前的，因為是對原始的，未經過激活的logit數據進行數據分布的重整。然而，不少實驗證實似乎BN層放在激活層之后效果會更好，這個原因目前不明。Update 2020/5/18: 在新的文獻[28]中，作者嘗試解釋了以下BN用法的原因，有興趣的讀者可以移步去細讀下。 傳統用法:

graph LR weights --> BatchNorm BatchNorm --> ReLU [28]的作者提出的用法：

graph LR ReLU --> BatchNorm+dropout BatchNorm+dropout --> weights 15、dropout層應用在卷積層中可能導致更差的性能 dropout[19]是hinton大神與2012年提出的一種神經網絡正則手段，其可以簡單解釋為在訓練過程中，按一定概率讓神經網絡中的某些神經元輸出為0，其原因可以有幾個解釋，一個是作為一種集成模型進行解釋，另一個可以看成是在特征提取學習過程中給數據加入噪聲，可以看成是一種數據增強的正則手段。 在原始論文中，dropout被應用于全連接層中，而沒有應用在卷積層中，Hinton的解釋是因為卷積層參數并不多，過擬合風險較小不適合采用dropout這種大殺器的正則手段。有人也認為因為卷積網絡是局部感知的，用dropout正則對于其在后層中對于全局信息的獲取可能具有負作用[20]。 不過在一些工作中，也有人將dropout層應用在卷積層中的[17-18]，其層次安排為:，不過其丟棄率都是選擇的較小數如，等，個人覺得這里的作用大概是對中間數據進行加入噪聲，以便于數據增強的正則手段。個人建議是可以嘗試在卷積層中使用少量的dropout，用較小的丟棄率，但是最后別忘了扔掉這些dropout再進行一些探索，也許可以具有更好的效果。 16、較小的batch size可以提供較好的泛化 現代的深度學習優化器基本上都是基于SGD算法進行修改而成的，在每一次訓練中都是以一個batch size為單位進行訓練的，在這個過程中相當于在統計這個batch中樣本的一些統計特性，因此batch size是會影響模型的超曲線形狀的。 一般來說較大的batch size比如128，256會和整個訓練集的統計性質更相近，從而使得具有較少的多樣性，而較小的batch size 比如16，32，因為batch size較小，不同batch之間的差異性較大，這種差異性可以看成是正則手段，有機會提高模型的泛化性能。（不過有些文章似乎不同意這個觀點，認為較大batch size有較好性能，個人建議是大batch size和小batch size都可以跑跑，有可能能提升性能。） 17、初始化權值不能初始化為全0 這個應該是老生常談了，但是初學者經常會出現這種錯誤，在初始化權值的時候將權值全部初始化為了0，在反向傳播的過程中，對于某個權值的更新公式為[22]： 這個公式推導具體參見[22]，這里不累述了，我們可以發現，當初始化權值參數全部為0的時候，我們的將全部為0，這個時候對于某個權值的梯度也就變為了0，因此整個網絡的任何參數都得不到更新，將會導致訓練無法進行。 而對于偏置的初始化不同，對于偏置的更新公式如[22]： 我們可以發現，對于偏置的更新而言，不依賴與初始值，因此偏置的初始化可以初始化為全0。 18、別忘了你的偏置 這個也是初學者很容易犯的錯誤，就是忘記給每一層添加偏置。我們在筆記第二點中提到了神經網絡中偏置的作用，總的來說就是對超平面進行平移的，因此一般來說，我們的神經網絡都是需要添加偏置的，不然你的超平面就只能是通過原點的了，這樣大大減少了模型的容量，經常會使得模型欠擬合。 19、驗證準確率遠大于測試準確率 有些時候，你發現你的驗證集準確率遠大于測試集的準確率，在排除了代碼問題和操作問題之后，其實也可能是因為訓練集和測試集劃分的問題。一般來說，你的驗證集是從訓練集中劃分出來的[23]，因此你的驗證集和訓練集可以視為是同分布的，但是并不能確保你的訓練集和測試集是同分布的，如果訓練集和測試集的分布差的比較大，就可能出現這種情況。這個時候，可以考慮遷移學習中的一些方法。 20、KL散度出現負數 Kullback–Leibler散度，簡稱KL散度[24]，也稱為相對熵，是一種用于度量兩個分布之間相似性的常用手段，公式如(20.1)，其中第二行形式的變形描述了相對熵的特性。 我們注意到KL散度是不可能為負數的，其中是定義在同一個概率空間[25]里面的同型的分布，維度相同。從相對熵的定義來看，這個公式描述了用分布去近似所造成的不一致性的程度。在深度學習和機器學習中，一般是用來描述兩個維度相同的概率分布之間的相似度。注意到，這里的都是概率分布，因此是需要經過softmax層的，才能保證概率和為1，不然可能會出現KL散度為負數的笑話。 而且，在一些框架如Pytorch中，其輸入值需要是log_softmax而目標值需要是softmax值，也就說輸入值需要進行對數操作后再轉變為概率分布[27]。