這篇文章對轉置卷積（反卷積）有著很好的解釋，這里將其翻譯為中文，以饗國人。

對于上采用的需求

當我們用神經網絡生成圖片的時候，經常需要將一些低分辨率的圖片轉換為高分辨率的圖片。

對于這種上采樣(up-sampling)操作，目前有著一些插值方法進行處理： 最近鄰插值(Nearest neighbor interpolation) 雙線性插值(Bi-Linear interpolation) 雙立方插值(Bi-Cubic interpolation) 以上的這些方法都是一些插值方法，需要我們在決定網絡結構的時候進行挑選。這些方法就像是人工特征工程一樣，并沒有給神經網絡學習的余地，神經網絡不能自己學習如何更好地進行插值，這個顯然是不夠理想的。

為什么是轉置卷積

轉置卷積(Transposed Convolution)常常在一些文獻中也稱之為反卷積(Deconvolution)和部分跨越卷積(Fractionally-strided Convolution)，因為稱之為反卷積容易讓人以為和數字信號處理中反卷積混起來，造成不必要的誤解，因此下文都將稱為轉置卷積，并且建議各位不要采用反卷積這個稱呼。 如果我們想要我們的網絡可以學習到最好地上采樣的方法，我們這個時候就可以采用轉置卷積。這個方法不會使用預先定義的插值方法，它具有可以學習的參數。理解轉置卷積這個概念是很重要的，因為它在若干重要的文獻中都有所應用，如： 1、在DCGAN中的生成器將會用隨機值轉變為一個全尺寸(full-size)的圖片，這個時候就需要用到轉置卷積。 2、在語義分割中，會使用卷積層在編碼器中進行特征提取，然后在解碼層中進行恢復為原先的尺寸，這樣才可以對原來圖像的每個像素都進行分類。這個過程同樣需要用到轉置卷積。

卷積操作

讓我們回顧下卷積操作是怎么工作的，并且我們將會從一個小例子中直觀的感受卷積操作。假設我們有一個的矩陣，我們將在這個矩陣上應用的卷積核，并且不添加任何填充(padding)，步進參數(stride)設置為1，就像下圖所示，輸出為一個的矩陣。

這個卷積操作在輸入矩陣和卷積核中，對每個元素的乘積進行相加。因為我們沒有任何填充和使用1為步進，因此我們只能對這個操作進行4次，因此我們的輸出矩陣尺寸為。

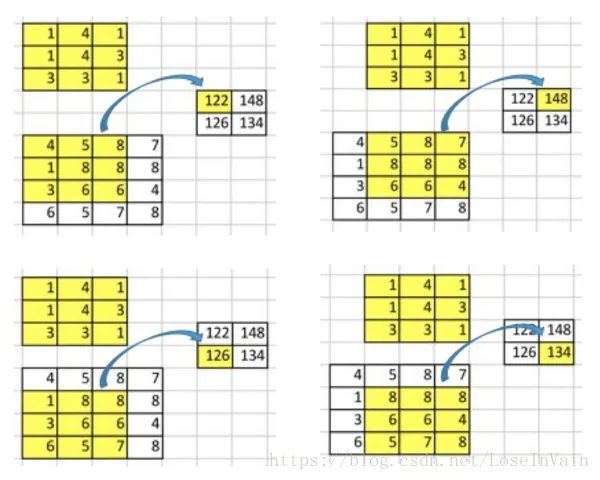
這種卷積操作使得輸入值和輸出值之間存在有位置上的連接關系，舉例來說，輸入矩陣左上方的值將會影響到輸出矩陣的左上方的值。更具體而言，的卷積核是用來連接輸入矩陣中的9個值，并且將其轉變為輸出矩陣的一個值的。一個卷積操作是一個多對一(many-to-one)的映射關系。讓我們記住這個，我們接下來將會用得著。

反過來操作吧

現在，假設我們想要反過來操作。我們想要將輸入矩陣中的一個值映射到輸出矩陣的9個值，這將是一個一對多(one-to-many)的映射關系。這個就像是卷積操作的反操作，其核心觀點就是用轉置卷積。舉個例子，我們對一個的矩陣進行上采樣為的矩陣。這個操作將會維護一個1對應9的映射關系。

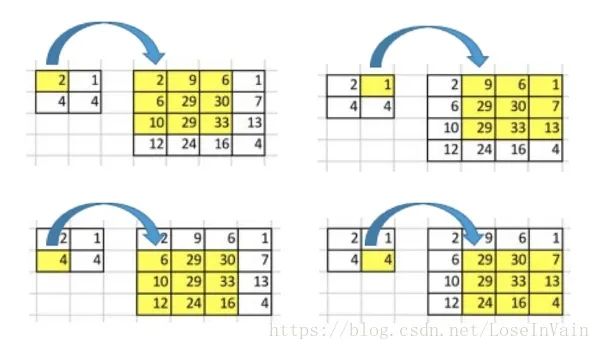
因此就結論而言，卷積操作是多對一，而轉置卷積操作是一對多，如下圖所示，每一個“對”而言，都需要維護一個權值。

但是我們將如何具體操作呢？為了接下來的討論，我們需要定義一個卷積矩陣(convolution matrix)和相應的轉置卷積矩陣(transposed convolution matrix)。

卷積矩陣

我們可以將一個卷積操作用一個矩陣表示。這個表示很簡單，無非就是將卷積核重新排列到我們可以用普通的矩陣乘法進行矩陣卷積操作。如下圖就是原始的卷積核：

我們對這個的卷積核進行重新排列，得到了下面這個的卷積矩陣：

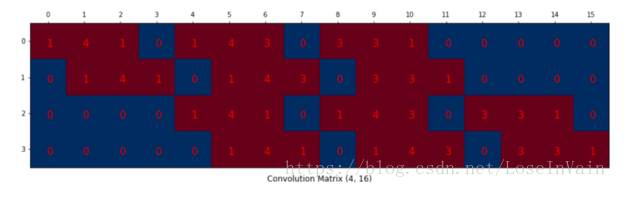
這個便是卷積矩陣了，這個矩陣的每一行都定義了一個卷積操作。下圖將會更加直觀地告訴你這個重排列是怎么進行的。每一個卷積矩陣的行都是通過重新排列卷積核的元素，并且添加0補充(zero padding)進行的。

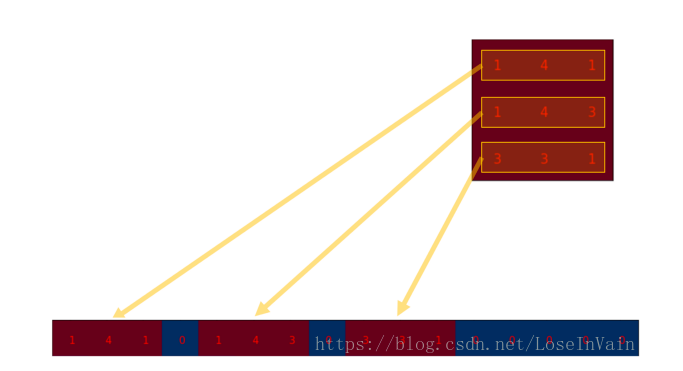
為了將卷積操作表示為卷積矩陣和輸入矩陣的向量乘法，我們將輸入矩陣攤平(flatten)為一個列向量，形狀為，如下圖所示。

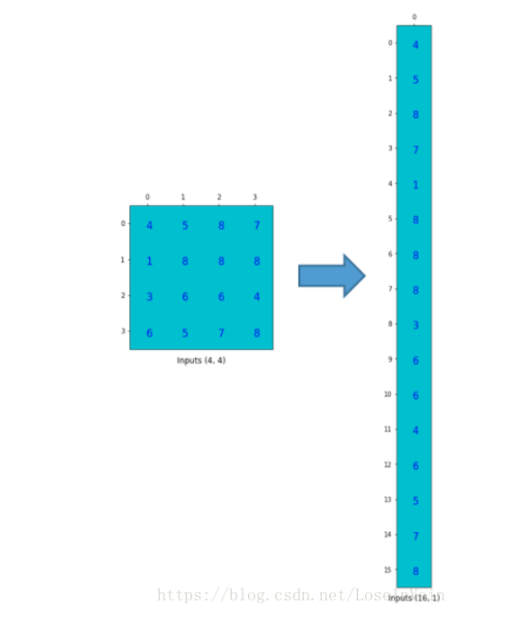
我們可以將這個的卷積矩陣和的輸入列向量進行矩陣乘法，這樣我們就得到了輸出列向量。

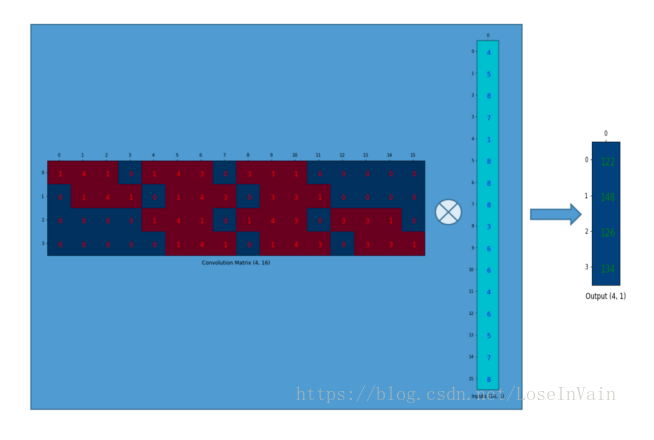
這個輸出的的矩陣可以重新塑性為一個的矩陣，而這個矩陣正是和我們一開始通過傳統的卷積操作得到的一模一樣。

簡單來說，這個卷積矩陣除了重新排列卷積核的權重之外就沒有啥了，然后卷積操作可以通過表示為卷積矩陣和輸入矩陣的列向量形式的矩陣乘積形式進行表達。 所以各位發現了嗎，關鍵點就在于這個卷積矩陣，你可以從16()到4()因為這個卷積矩陣尺寸正是的，然后呢，如果你有一個的矩陣，你就可以從4()到16()了，這不就是一個上采樣的操作嗎？啊哈！讓我們繼續吧！

轉置卷積矩陣

我們想要從4()到16()，因此我們使用了一個的矩陣，但是還有一件事情需要注意，我們是想要維護一個1到9的映射關系。 假設我們轉置這個卷積矩陣變為。我們可以對和列向量進行矩陣乘法，從而生成一個的輸出矩陣。這個轉置矩陣正是將一個元素映射到了9個元素。

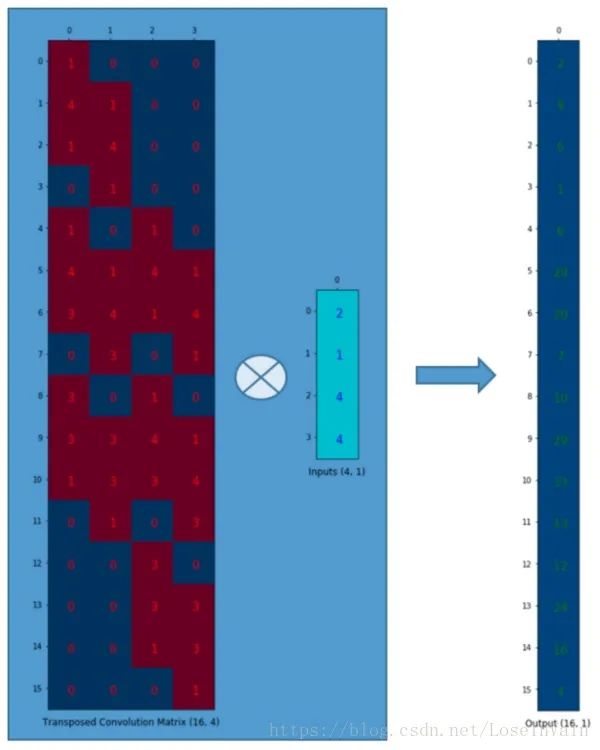
這個輸出可以塑形為的矩陣：

我們只是對小矩陣進行上采樣為一個更大尺寸的矩陣。這個轉置卷積矩陣維護了一個1個元素到9個元素的映射關系，因為這個關系正表現在了其轉置卷積元素上。需要注意的是：這里的轉置卷積矩陣的參數，不一定從原始的卷積矩陣中簡單轉置得到的，轉置這個操作只是提供了轉置卷積矩陣的形狀而已。

總結

轉置卷積操作構建了和普通的卷積操作一樣的連接關系，只不過這個是從反向方向開始連接的。我們可以用它進行上采樣。另外，這個轉置卷積矩陣的參數是可以學習的，因此我們不需要一些人為預先定義的方法。即使它被稱為轉置卷積，它并不是意味著我們將一些現存的卷積矩陣簡單轉置并且使用其轉置后的值。 從本質來說，轉置卷積不是一個卷積，但是我們可以將其看成卷積，并且當成卷積這樣去用。我們通過在輸入矩陣中的元素之間插入0進行補充，從而實現尺寸上采樣，然后通過普通的卷積操作就可以產生和轉置卷積相同的效果了。你在一些文章中將會發現他們都是這樣解釋轉置卷積的，但是這個因為在卷積操作之前需要通過添加0進行上采樣，因此是比較低效率的。注意：轉置卷積會導致生成圖像中出現棋盤效應(checkerboard artifacts)，這篇文章《Deconvolution and Checkerboard Artifacts》推薦了一種上采樣的操作（也就是插值操作），這個操作接在一個卷積操作后面以減少這種現象。如果你的主要目的是生成盡可能少棋盤效應的圖像，那么這篇文章就值得你去閱讀。