來源:卓晴
01問題提出
卓大大,我有一個問題想要請教。對于舵機的轉向控制,高速的時候需要動態P才能得到平滑的控制效果(也就是偏差越小P越小,偏差越大P越大)。
但對于電機的速度控制,在任何期望速度下,P參數不需要動態都可得到很好的效果,請問這個如何用理論解釋?是因為電機的慣性比較大嗎?
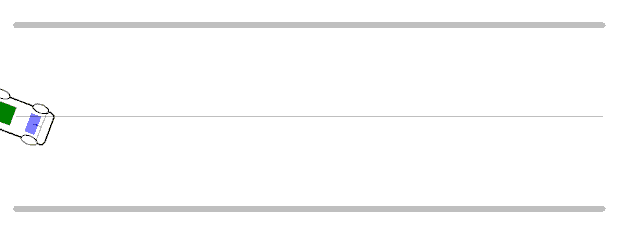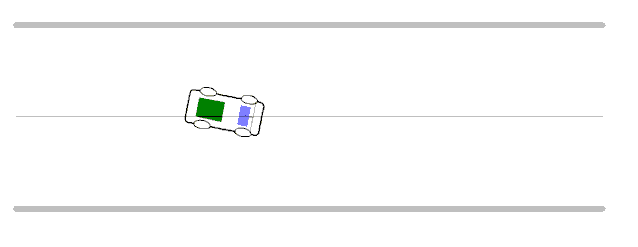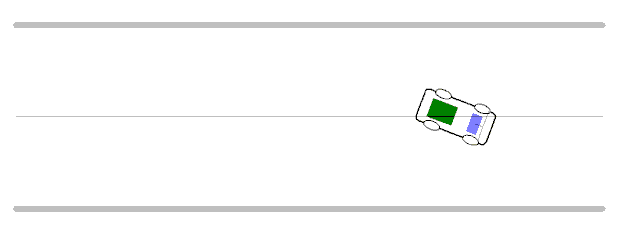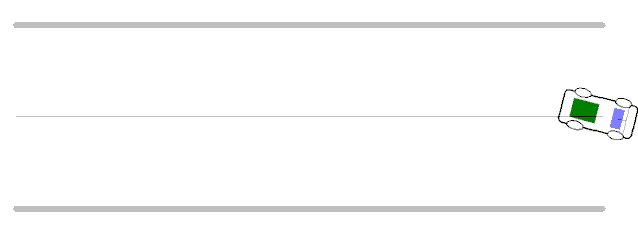
▲ 車模在不同速度下運行出現的振蕩
02理論分析
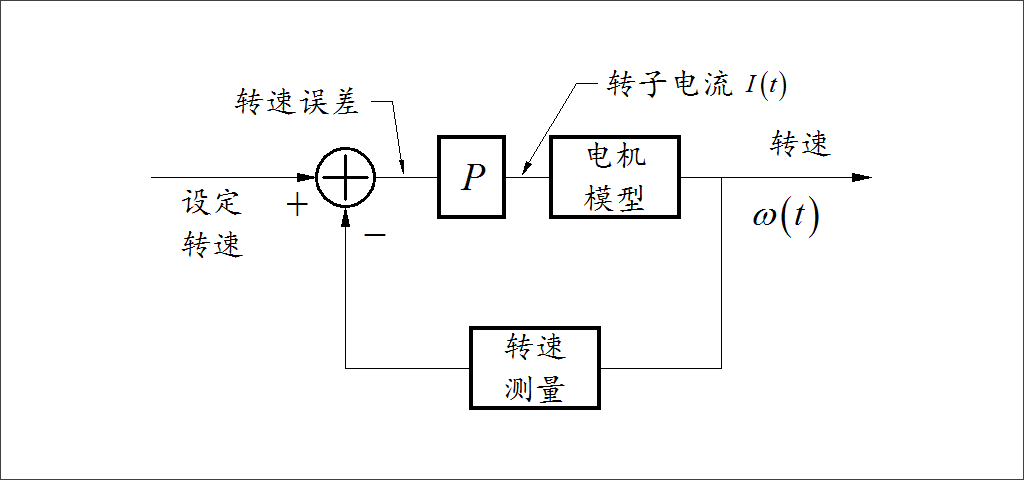
對于電機轉速 控制,如果采用電流串激閉環控制(這樣建模分析比較簡單),電機的轉速 的加速度正比于轉子力矩,轉子的力矩正比于轉子電流。因此如果控制速度環控制率采用比例控制,整個系統就是一個典型的二階控制系統。在電機帶有阻尼負載(即力矩與轉速成正比),該系統可以穩定,并且穩定性與轉速無關。這是因為整個系統反饋控制比例控制增益與轉速沒有關系。
對于車模在賽道上循跡運行控制時,舵機的輸出正比于車模前輪的轉角 。前輪轉角相對于車模位移 積分就形成車模與賽道線中心的偏移量 :
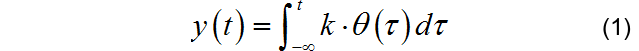
而位移 是車模速度 的積分:
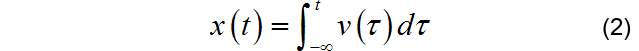
將(2)式代入(1)可以得到:
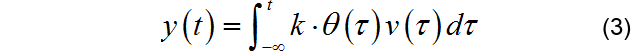
分析(3)可以看到,相對于舵機輸出角度 對于車模偏移量影響是一個積分關系,其中積分項系數包括 ,這一項與速度成正比。如果同樣使用比例負反饋來對車模偏移量進行控制的話,反饋比例系數與車模運行速度成正比。這一點與前面電機控制是不同的。
下圖顯示了車模運行速度 為恒速 時,車模的偏移量與舵機輸出轉角 之間的關系。
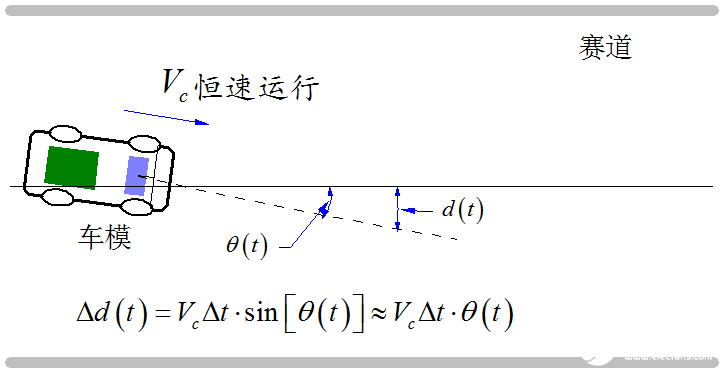
▲ 在恒速下,車模的偏移量與舵機輸出轉角之間的關系
考慮到車模的慣性以及舵機執行過程的延遲等特點,當車模方向控制比例超過一定限度后,方向控制就會變得不穩定了。
由此,可以知道車模方向比例控制的時候,需要根據車速調整比例系數。

▲ 車模在轉彎過程中的動態特性
03仿真實驗
由于舵機輸出轉角的轉動速度是有限值,而且近似為 一個恒速轉動,這是一個非線性的環節。為了簡化分析,下面將舵機簡化成一個純延遲環節。比如延遲100ms。將這個延遲環節重新增加在上面的仿真系統中,就會發現,隨著比例控制的增加增加,系統的單位階躍響應就會變得不穩定。
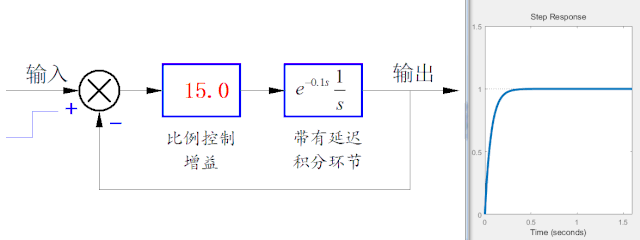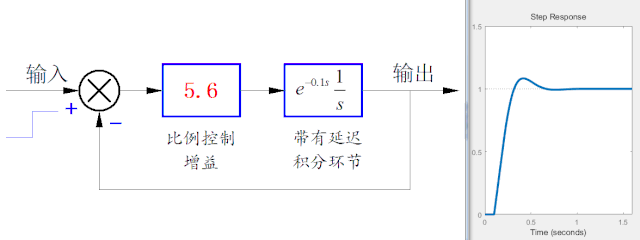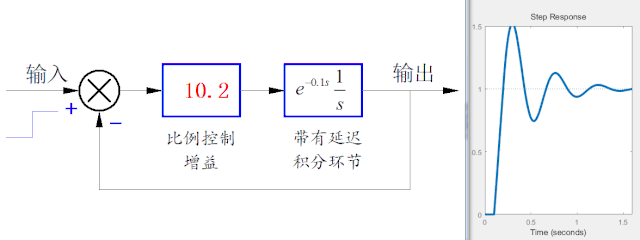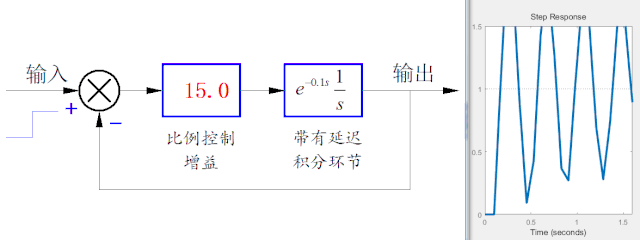
▲ 帶有純延時環節的一階積分環節的比例控制
通過上面的仿真可以看出,比例增益過大會使得系統變得越來越不穩定。根據02節敘述的,車模方向控制的比例系數是與車速成正比,所以當車速增加時,車模運行就會變得原來也不穩定了。
04如果解決方向不穩定?
解決車模方向控制不穩定的方法:
動態調整控制參數,比如車速增加時,需要適當減少P的大小,從而抑制振蕩的產生。這種方法在直道運行是比較有效果,但在彎道時,車模軌跡就會距離賽道中心線有較大的偏差。
通過增加賽道檢測的 前瞻距離,也就是將車模相對賽道的偏差位置盡可能往前移,這樣就可以抵消舵機執行過程中所帶來的時間延遲。使用攝像頭可以有效提高賽道前方檢測的距離。
通過機器學習的方法進行賽道預測。由于賽道元素的組合是有限的,并且是提前公布的。可以通過機器學習的方法將賽道偏移控制信息存儲在人工神經網絡中,來提高控制的精度。比如今年AI電磁組,雖然賽道檢測的電感傳感器非常短,但是經過機器學習也可以獲得與攝像頭相近的性能。
提高舵機的性能。舵機的慣性(延遲)是造成方向控制不穩定的內因。可以適當通過改造舵機輸出機械連桿,增加它的機械傳動比例,可以在一定程度上提高車模控制的快速性。
在控制算法中引入微分量,來抑制振蕩的現象。
下圖是通過在控制環節中引入微分控制項,可以看到微分系數在一定范圍內可以減少系統輸出的振蕩。但是當微分系數過大時,也會引起系統的不穩定性。
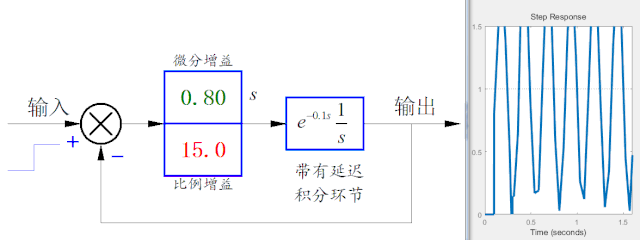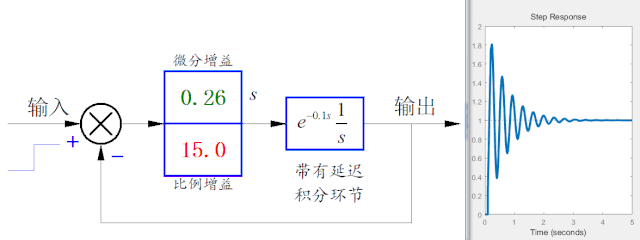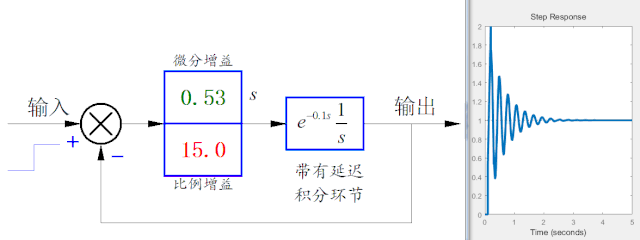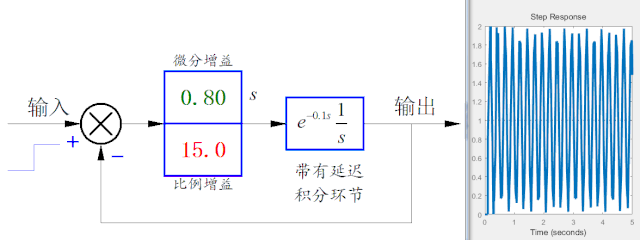
▲ 增加控制中的微分項,在一定參數范圍內可以抑制振蕩
[1]劈-I-D: https://zhuoqing.blog.csdn.net/article/details/104134875
-
電機
+關注
關注
142文章
8938瀏覽量
145123 -
舵機
+關注
關注
17文章
265瀏覽量
40958 -
智能車模
+關注
關注
0文章
7瀏覽量
6764
發布評論請先 登錄
相關推薦
深控技術研發的“不需要點表的工業數據采集網關”支持起1100種行業協議

深控技術研發的 “不需要點表的工業網關” 在 CNC 采集方面的應用

不需要點表的工業網關應用案例:如何提升工業企業生產效率與質量?

不需要點表的 PLC 工業網關 在印刷 / 包裝行業的實施案例

C語言為什么不需要包含stdio.h
基于 “不需要點表的工業網關” 的工業自動化設備遠程監控解決方案

深控技術研發的 “不需要點表的工業網關” 在工廠產線設備的應用





 為什么P參數不需要動態都可得到很好的效果?
為什么P參數不需要動態都可得到很好的效果?










評論