Q-Learning這一篇對應Sutton書的第六章部分和UCL強化學習課程的第五講部分。
1. Q-Learning算法的引入
Q-Learning算法是一種使用時序差分求解強化學習控制問題的方法,回顧下此時我們的控制問題可以表示為:給定強化學習的5個要素:狀態集SS, 動作集AA, 即時獎勵RR,衰減因子γγ, 探索率??, 求解最優的動作價值函數q?q?和最優策略π?π?。
這一類強化學習的問題求解不需要環境的狀態轉化模型,是不基于模型的強化學習問題求解方法。對于它的控制問題求解,和蒙特卡羅法類似,都是價值迭代,即通過價值函數的更新,來更新策略,通過策略來產生新的狀態和即時獎勵,進而更新價值函數。一直進行下去,直到價值函數和策略都收斂。
再回顧下時序差分法的控制問題,可以分為兩類,一類是在線控制,即一直使用一個策略來更新價值函數和選擇新的動作,比如我們上一篇講到的SARSA, 而另一類是離線控制,會使用兩個控制策略,一個策略用于選擇新的動作,另一個策略用于更新價值函數。這一類的經典算法就是Q-Learning。
對于Q-Learning,我們會使用????貪婪法來選擇新的動作,這部分和SARSA完全相同。但是對于價值函數的更新,Q-Learning使用的是貪婪法,而不是SARSA的????貪婪法。這一點就是SARSA和Q-Learning本質的區別。
2. Q-Learning算法概述
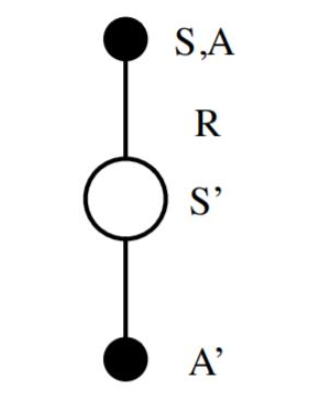
Q-Learning算法的拓補圖入下圖所示:
首先我們基于狀態SS,用????貪婪法選擇到動作AA, 然后執行動作AA,得到獎勵RR,并進入狀態S′S′,此時,如果是SARSA,會繼續基于狀態S′S′,用????貪婪法選擇A′A′,然后來更新價值函數。但是Q-Learning則不同。
對于Q-Learning,它基于狀態S′S′,沒有使用????貪婪法選擇A′A′,而是使用貪婪法選擇A′A′,也就是說,選擇使Q(S′,a)Q(S′,a)最大的aa作為A′A′來更新價值函數。用數學公式表示就是:

對應到上圖中就是在圖下方的三個黑圓圈動作中選擇一個使Q(S′,a)Q(S′,a)最大的動作作為A′A′。
此時選擇的動作只會參與價值函數的更新,不會真正的執行。價值函數更新后,新的執行動作需要基于狀態S′S′,用????貪婪法重新選擇得到。這一點也和SARSA稍有不同。對于SARSA,價值函數更新使用的A′A′會作為下一階段開始時候的執行動作。
下面我們對Q-Learning算法做一個總結。
3. Q-Learning算法流程
下面我們總結下Q-Learning算法的流程。
算法輸入:迭代輪數TT,狀態集SS, 動作集AA, 步長αα,衰減因子γγ, 探索率??,
輸出:所有的狀態和動作對應的價值QQ1. 隨機初始化所有的狀態和動作對應的價值QQ. 對于終止狀態其QQ值初始化為0.
2. for i from 1 to T,進行迭代。
a) 初始化S為當前狀態序列的第一個狀態。
b) 用????貪婪法在當前狀態SS選擇出動作AA
c) 在狀態SS執行當前動作AA,得到新狀態S′S′和獎勵RR
d) 更新價值函數Q(S,A)Q(S,A):

e) S=S′S=S′
f) 如果S′S′是終止狀態,當前輪迭代完畢,否則轉到步驟b)
4. Q-Learning算法實例:Windy GridWorld
我們還是使用和SARSA一樣的例子來研究Q-Learning。如果對windy gridworld的問題還不熟悉,可以復習強化學習(六)時序差分在線控制算法SARSA第4節的第二段。
完整的代碼參見我的github: https://github.com/ljpzzz/machinelearning/blob/master/reinforcement-learning/q_learning_windy_world.py
絕大部分代碼和SARSA是類似的。這里我們可以重點比較和SARSA不同的部分。區別都在episode這個函數里面。
首先是初始化的時候,我們只初始化狀態SS,把AA的產生放到了while循環里面, 而回憶下SARSA會同時初始化狀態SS和動作AA,再去執行循環。下面這段Q-Learning的代碼對應我們算法的第二步步驟a和b:
# play for an episode
def episode(q_value):
# track the total time steps in this episode
time = 0
# initialize state
state = START
while state != GOAL:
# choose an action based on epsilon-greedy algorithm
if np.random.binomial(1, EPSILON) == 1:
action = np.random.choice(ACTIONS)
else:
values_ = q_value[state[0], state[1], :]
action = np.random.choice([action_ for action_, value_ in enumerate(values_) if value_ == np.max(values_)])
接著我們會去執行動作AA,得到S′S′, 由于獎勵不是終止就是-1,不需要單獨計算。,這部分和SARSA的代碼相同。對應我們Q-Learning算法的第二步步驟c:
next_state = step(state, action)
def step(state, action):
i, j = state
if action == ACTION_UP:
return [max(i - 1 - WIND[j], 0), j]
elif action == ACTION_DOWN:
return [max(min(i + 1 - WIND[j], WORLD_HEIGHT - 1), 0), j]
elif action == ACTION_LEFT:
return [max(i - WIND[j], 0), max(j - 1, 0)]
elif action == ACTION_RIGHT:
return [max(i - WIND[j], 0), min(j + 1, WORLD_WIDTH - 1)]
else:
assert False
后面我們用貪婪法選擇出最大的Q(S′,a)Q(S′,a),并更新價值函數,最后更新當前狀態SS。對應我們Q-Learning算法的第二步步驟d,e。注意SARSA這里是使用????貪婪法,而不是貪婪法。同時SARSA會同時更新狀態SS和動作AA,而Q-Learning只會更新當前狀態SS。
values_ = q_value[next_state[0], next_state[1], :]
next_action = np.random.choice([action_ for action_, value_ in enumerate(values_) if value_ == np.max(values_)])
# Sarsa update
q_value[state[0], state[1], action] += \
ALPHA * (REWARD + q_value[next_state[0], next_state[1], next_action] -
q_value[state[0], state[1], action])
state = next_state
跑完完整的代碼,大家可以很容易得到這個問題的最優解,進而得到在每個格子里的最優貪婪策略。
5. SARSA vs Q-Learning
現在SARSA和Q-Learning算法我們都講完了,那么作為時序差分控制算法的兩種經典方法嗎,他們都有說明特點,各自適用于什么樣的場景呢?
Q-Learning直接學習的是最優策略,而SARSA在學習最優策略的同時還在做探索。這導致我們在學習最優策略的時候,如果用SARSA,為了保證收斂,需要制定一個策略,使????貪婪法的超參數??在迭代的過程中逐漸變小。Q-Learning沒有這個煩惱。
另外一個就是Q-Learning直接學習最優策略,但是最優策略會依賴于訓練中產生的一系列數據,所以受樣本數據的影響較大,因此受到訓練數據方差的影響很大,甚至會影響Q函數的收斂。Q-Learning的深度強化學習版Deep Q-Learning也有這個問題。
在學習過程中,SARSA在收斂的過程中鼓勵探索,這樣學習過程會比較平滑,不至于過于激進,導致出現像Q-Learning可能遇到一些特殊的最優“陷阱”。比如經典的強化學習問題“Cliff Walk”。
在實際應用中,如果我們是在模擬環境中訓練強化學習模型,推薦使用Q-Learning,如果是在線生產環境中訓練模型,則推薦使用SARSA。
6. Q-Learning結語
對于Q-Learning和SARSA這樣的時序差分算法,對于小型的強化學習問題是非常靈活有效的,但是在大數據時代,異常復雜的狀態和可選動作,使Q-Learning和SARSA要維護的Q表異常的大,甚至遠遠超出內存,這限制了時序差分算法的應用場景。在深度學習興起后,基于深度學習的強化學習開始占主導地位,因此從下一篇開始我們開始討論深度強化學習的建模思路。
編輯:hfy
-
Q-Learning
+關注
關注
0文章
5瀏覽量
8100 -
深度學習
+關注
關注
73文章
5493瀏覽量
120983 -
SARSA
+關注
關注
0文章
2瀏覽量
1314
發布評論請先 登錄
相關推薦
基于差分演化算法的PID參數優化算法
基于Q-Learning的認知無線電系統感知管理算法
基于LCS多機器人的算法介紹
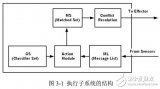
兼具動態規劃DP和蒙特卡洛MC優點的TD Learning算法
基于Q-learning的碼率控制算法
強化學習究竟是什么?它與機器學習技術有什么聯系?
關于TD Learning算法的分析
Q Learning算法學習
強化學習的雙權重最小二乘Sarsa算法

基于雙估計器的Speedy Q-learning算法
可改善小區網絡通信干擾問題的HSARSA算法
7個流行的強化學習算法及代碼實現
7個流行的強化學習算法及代碼實現





 淺談Q-Learning和SARSA時序差分算法
淺談Q-Learning和SARSA時序差分算法










評論