作者：romme

1、圖像直方圖概念

圖像直方圖用來反映一副圖像的像素分布。其中，橫坐標表示圖像像素的灰度級，縱坐標表示每個灰度級對應的像素總數或占所有像素個數的百分比。

例如：灰度級為[0~255]的數字圖像直方圖，定義：

h（rk）= nk

其中，rk是第k個灰度級（k = 0~255），nk是該灰度級的個數。

若以每個灰度級的個數nk去除以圖像像素總數n，則得到歸一化的直方圖，定義：

P（rk）= nk/n

即，P（rk）表示灰度級為rk發生的概率估計值。所以：一個歸一化直方圖，其所有部分之和應等于1。

2、為什么要做直方圖均衡化

在圖像處理應用中，若得到這樣一副圖片，其圖像的灰度分布集中在較窄的范圍內，那么視覺上就給人感覺，對比度較差，細節不夠清晰。為了使圖像變得清晰，就需要提升對比度。

如何提升對比度呢？即，對圖像進行非線性拉伸，使得圖像的灰度分布變寬，灰度值分布變得均勻。這樣，在灰度級范圍內，像素的個數分布大致相同，就會使得圖像的對比度增強，細節更清晰。

那么，又如何使得灰度值分布均勻呢？即，直方圖均衡化。

3、直方圖均衡化原理

直方圖均衡化，即將隨機分布的圖像直方圖修改成均勻分布的直方圖。

基本思想：對原始圖像的像素灰度做某種映射變換，使變換后圖像灰度的概率密度呈均勻分布。這就意味著圖像灰度的動態范圍得到了增加, 提高了圖像的對比度。

作用：圖像增強。

那么，我們使用哪種映射變換呢？答案是：累積分布函數。

說明：

①為什么要選用累積分布函數？

②為什么使用累積分布函數處理后，像素值會均勻分布？

直方圖均衡化，必須保證：

①像素值經過映射變換后，原本的大小關系不能發生改變。即較亮的區域，依舊較亮；較暗的區域，依舊較暗。只是增大了對比度，絕對不能明暗顛倒，否則就不是原本的圖像了。

②像素值經過映射變換后，不能越界。例如：8bit圖像，像素值范圍0~255；12bit圖像，像素值0~4095。

由于累積分布函數是單調遞增函數，可以滿足條件①；又因為累積分布函數的值域為0~1，可以控制越界，滿足條件②。

實則，有嚴謹的數學推導過程，在此直接給出公式，具體可以參考《數字圖像處理---岡薩雷斯》一書。

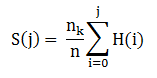
其中，H(i)表示圖像直方圖，nk/n表示歸一化。

所以，直方圖均衡化實現過程：

（1）求圖像直方圖；（統計直方圖每個灰度級出現的次數）

（2）做歸一化處理；

（3）計算新的像素值。

4、FPGA實現

FPGA實現的核心在于算法，弄清楚原理，寫代碼只是一個機械的過程。假設一副圖像：2464x2056, 8bit，即共有5065984個像素點，256個灰度級。參照上述直方圖均衡化的步驟，用FPGA實現，效果展示如下：

編輯：hfy