『模擬電子技術的基礎內容』

單相橋式整流濾波電路是“直流電源”系統中常見的、經典的電路，本文側重于分析其中電容濾波電路的運行過程，詳細回顧電容在其中是如何發揮作用的。

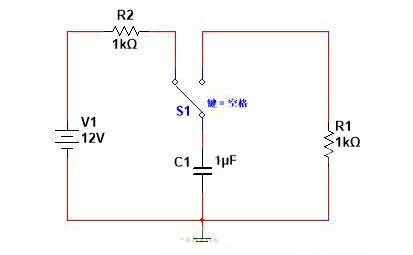
圖1 電容充放電電路

在開啟本文內容之前，我們先來看一下經典的電容試驗。

電容充放電試驗

圖1電路中直流電壓源V1=12V，電阻R2=1kΩ，開關S1，電容C1=1μF，電阻R1=1kΩ，

開關S1可以在左右兩個電路中來回切換。

圖2 電容的充電動態圖，來源網絡。

毫無疑問，S1閉合左邊電路之時，電壓源V1向C1充電，直至C1兩端電壓達到一定值后停止充電，此時：

電容兩端電壓+電阻R2兩端電壓=電源V1電壓12V。

在仿真電路中，我們可以驗證如下：

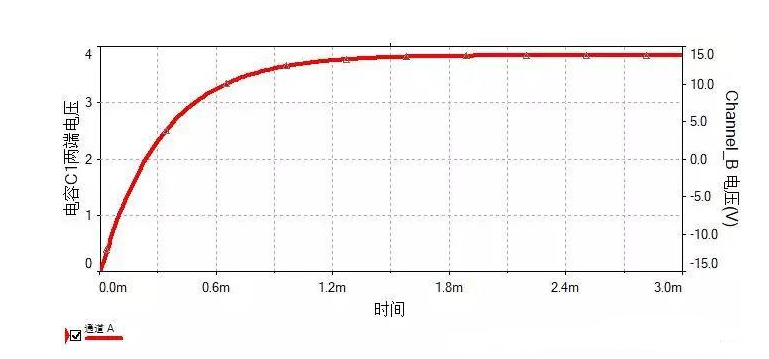
圖3 電容充電過程中兩端電壓變化曲線

從圖3中紅色的曲線即為電容兩端的電壓變化情況，橫坐標軸為時間軸，縱坐標軸為電壓值。

電容充電曲線以指數規律形式上升，大概3ms后達到最大值，約為3.87V。

圖3 電容的放電過程，來源網絡

如果此時開關撥向右邊電路，那么電容會將自己“體內”滿滿的電荷流向電阻R1。這個流動過程，叫做放電，見圖3。

進行定量分析。

『分析的過程中，使用了基爾霍夫定律和齊次微分方程的解法，這些在《電路》和《高等數學》都有介紹』

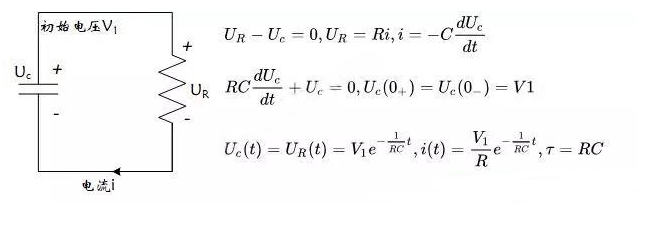
圖4 RC零輸入響應

推導過程可以不用太在意，關鍵看下我們的結論的，見圖4。

電阻兩端的電壓UR（t）和iR（t）隨著時間都是按照指數規律變化。同時，根據指數函數的性質，當時間為0時，函數取最大值V1和V1/R；

當時間趨向無窮大時，得到電壓和電流值為0。

令τ=RC

指數函數變化的快慢，與τ有關，τ值越大，函數變化越平緩，放電速度越慢；

τ值越小，函數變化越陡峭，放電速度越快。

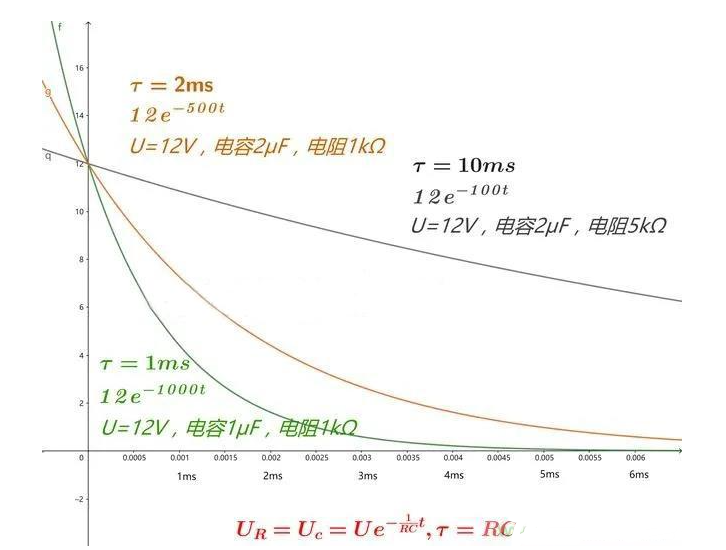
圖5 不同τ的指數曲線

我們可以通過圖5看出，指數函數與τ取值的關系。

當τ=1ms時，為圖5中的綠色曲線；

當τ=2ms時，為圖5中的紅色曲線；

當τ=10ms時候，為圖5中的黑色曲線；

我們通常認為當時間為3~5個τ的時候，電壓與電流值已經基本為0了，此時認為放電結束。

加上示波器，我們可以看下實際的波形。

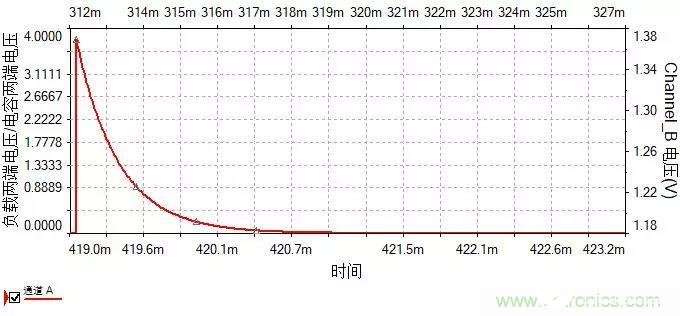
圖6 電容放電曲線

波形的確是按照指數規律下降，我們看到從419ms電壓開始下降，423ms差不多電壓趨于平緩。

『小結』

電容兩端電壓不能突變，在并聯電路中可以起到穩定電壓的作用；

如果你的電壓沒有我電容的高，那么我就對你充電，直至和我保持一樣；

如果你的電壓比我高，那你就對我充電，直至我的電壓和你保持一致；

流過電容的電流與電容兩端電壓的變化率成正比，Ic=CdUc/dt。

電壓變化越快，電流越大。

電容濾波電路

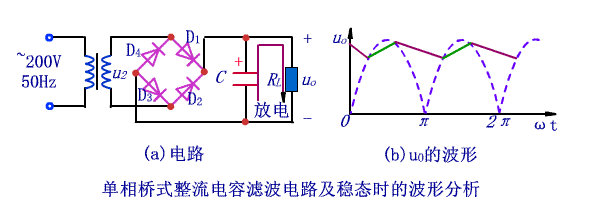
圖7 單相橋式整流電容濾波電路及輸出波形，來源網絡

圖7的電路，我們應該很熟悉，因為在前面單獨一文說過整流電路：

交流變直流，二極管整流電路是如何工作的？

這里的變化就是加了一個電容C。

如果不加電容C，輸出uo的波形就是圖7（b）的半波正弦（虛線）。那么現在電容C過來，它必然要發揮作用。

沒錯，就是保持電壓的作用。

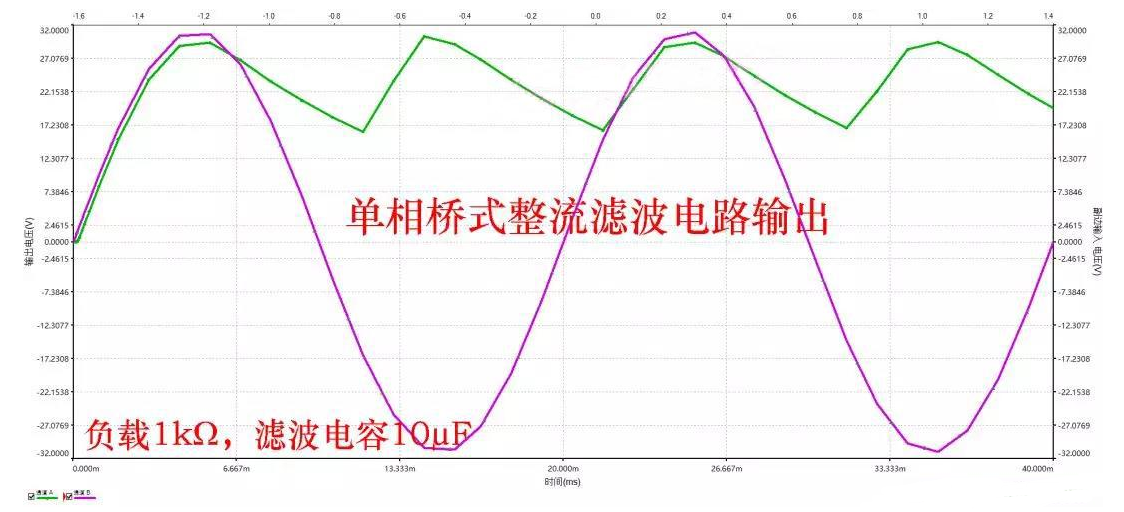
圖8 實際的電壓輸出波形

圖8中紅色曲線為副邊電壓u2的波形，綠色曲線為電路輸出電壓uo波形。

㈠當副邊電壓u2處于正弦波形正半周的時候，二極管D1、D3導通，此時對電容C先充電，如圖7（b）中的綠色曲線。（理想情況下，變壓器副邊無損耗，二極管導通電壓為零）

㈡隨之時間的推進，當副邊電壓u2上升到峰值后開始下降，電容通過負載電阻RL放電，其電壓uc也開始下降。

㈢繼續，當輸入電壓u2在某一時刻開始小于電容C電壓的時候（圖8中綠色與紅色曲線的交點），此時二極管D1、D3反向截止。電容C繼續通過RL放電，如圖（b）中的綠色折線。

㈣當u2的負半周幅度值變化到恰好大于uc時，D2、D4因正向電壓變為導通狀態，u2再次對C充電，uc上升到u2的峰值后又開始下降；下降到一定數值時D2、D4變為截止，C對RL放電，按指數規律下降；放電到一定數值時，D1、D3變為導通，重復上述過程。

具體的動態過程可以看圖7（b）。

這個波形看起來，不像單相橋式整流電路那么“震蕩”，交流成分明顯減少。

我們也知道，電容通交流（高頻），阻直流（低頻），所以一旦和負載RL并聯，必然交流高頻部分直接被電容過濾掉，所以這個電容也叫作旁路電容，因為它在“旁邊”。

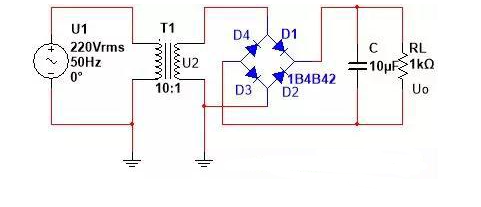
圖9 仿真電路

『主要特點』

㈠減少輸出直流電壓的脈動程度，提高了輸出電壓的平均值。

㈡電容放電時，回路電阻RL，放電時間常數為RLC，通常遠大于充電的時間常數。電容越大，負載電阻越大，濾波后輸出電壓越平滑，并且其平均值越大。

㈢通過計算（將圖9近似用折線替代），電容濾波電路輸出電壓的平均值可以達到1.2U2，電容承受的電壓為√2U2，考慮到電網電壓存在10%的波動，因此電容的耐壓值應大于1.1√2U2。

圖10 不同RlC的輸出波形比較

㈣在實際的電路中，選擇的濾波電容的容量一般需要滿足RLC=3~5T/2，其中T為電網電壓的周期（如果電網電壓為50Hz，那么周期T為20ms）

㈤輸出電壓隨著負載電流增大（負載電阻變小）而下降——帶負載的能力低。適用于輸出電壓高，負載小且變化少的場合。

㈥如果負載電阻無窮大，開路，電容不放電，輸出電壓√2U。

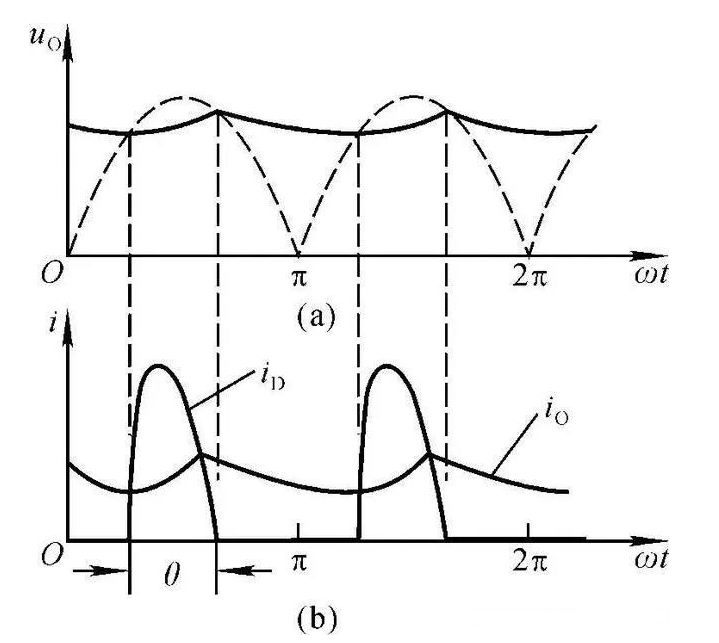
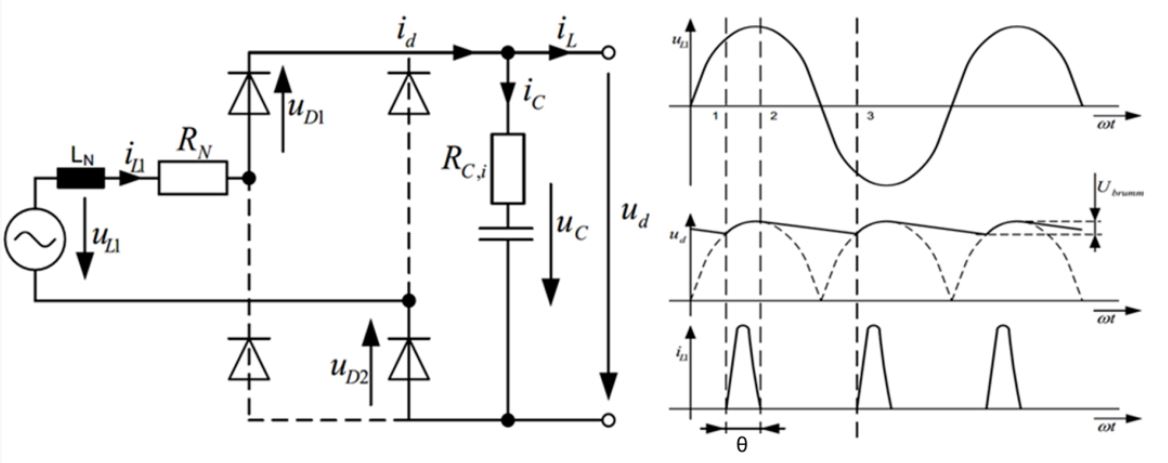
圖11 電容濾波電路中二極管的電流和導通角

我們知道，如果沒有加這個電容，那么橋式整流電路的中的二極管均有半個周期處于導通狀態，稱其導通角為θ等于π。

但是，一旦加上了濾波電容C，只有在給電容充電的時候，二極管才導通，所以每只二極管的導通角都要小于π了。

RLC如果取值較大，那么電容放電折線越“平緩”，濾波效果越好，電容充電時間也就越短，所以導通角θ越小。

觀察圖11（b），輸出電流為io，iD電流為整流二極管電流。根據基爾霍夫定律，我們可以認為iD=io+iC。

由于導通時間很短，所以要在短時間內產生io，必須電容充電電流iC很大（電容兩端電壓變化率很大），所以機會造成iD短時間內很大。

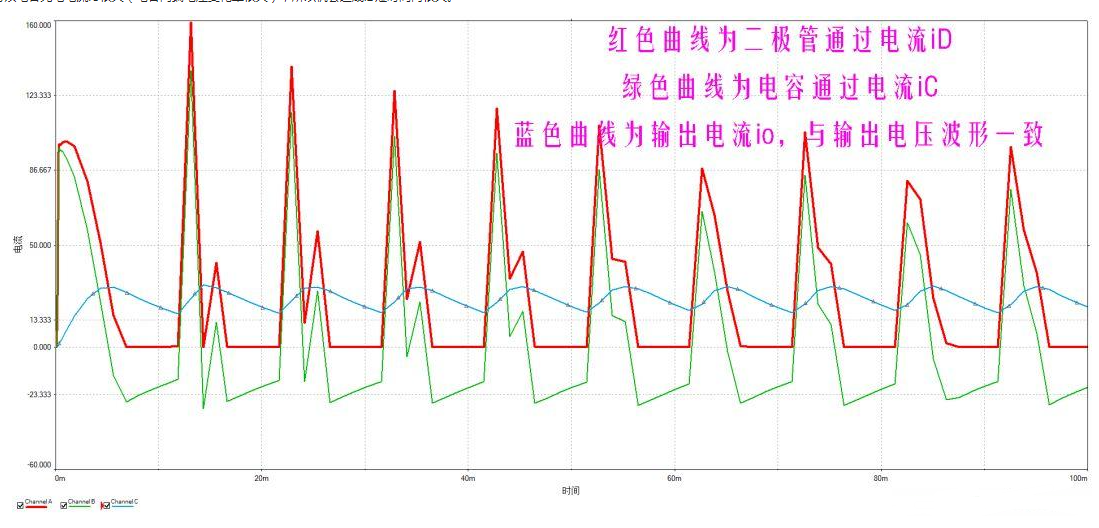
圖12 電容濾波電路的電流值分析

通過圖12，我們可以看出實際的電流波形，比理想的圖11要復雜的多。二極管的沖擊電流非常大。

電感濾波

在大電流的負載情況下，由于負載電阻RL很小，如果使用了電容濾波電路，想要保持“平滑”的電壓輸出效果，必然要提高電容C，因此電容容量需要很大，這個時候電容器和整流管都不太好選擇。

此時可以采用電感濾波電路。

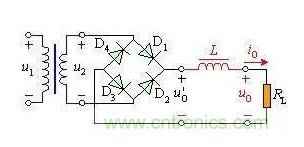
圖13 電感濾波電路

電感的感抗隨著交流頻率的增大而增大，它就阻礙了交流成分的通過。

同時電感線圈上，利用它的感應電動勢eL=-Ldi/dt，阻礙電流的變化，減少了對二極管的沖擊作用，頻率越高，感抗越大， 濾波效果就越好。

同時，由于濾波電感電動勢的作用，二極管的電流不可能像圖12那樣尖峰突變，必然要平緩很多。

所以電感濾波的二極管的導通角可以等于π，減少了二極管的沖擊電流，延長使用壽命。

總結

實際的工作中，通常采用復式濾波電路，結合電容和電感的特點進行組合，包括LC濾波電路、LCπ型濾波電路，RCπ型濾波電路。

各種濾波電路主要考慮三個參數，分別為脈動系數、二極管導通角、帶負載能力。具體的內容不再一一介紹，感興趣的同學可以自行查閱相關資料哦。

編輯：hfy