這是工作中遇到的小問題。
數據結構中有一種數據類型——堆棧,該結構中的數據項有如下特點:
除了最前面和最后面的數據,每個數據項都有一個前驅結點和一個后繼結點;
堆棧兩端分別稱為棧頂和棧底,數據項只能在棧頂加入或者彈出。
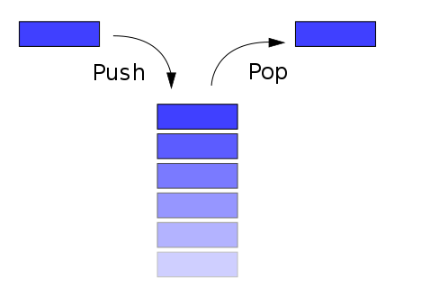
很明顯,堆棧的數據遵循先入后出原則。假設我們有 3 個不同的數據項,編號 1,2,3,只要保證入棧順序是大編號在后小編號在前,且每次進棧的數量不限,則所有可能的出棧順序有:1-》2-》3,1-》3-》2,2-》1-》3,2-》3-》1,3-》2-》1 一共 5 種,注意 3-》1-》2 不是可能的出棧順序,因為如果 3 最先出棧,那么 1 和 2 必在棧中(如果還未入棧,則說明 3 先入棧,與假設矛盾),只能 2 在上 1 在下,所以出棧順序必然是 2-》1。那么,
問題一:編號\(1\sim n\)的連續數據項以編號的先后順序入棧然后出棧,所有可能的出棧順序有多少種?
上面的問題比較難于回答,引申之后得到另一個比較弱的問題
問題二:給定一個長度為\(n\) 的整數序列,且各個元素均不相同,它是否是一個出棧序列?
為了回答以上的兩個問題,我們首先來看下一個正常的出棧序列有什么特點。假設長度為 \(n\)的出棧序列是\(a_1,a_2,…,a_n\),取其中第\(k\) 個數 \(a_k\),則有如下結論:
\(a_k\)之前的所有數據項都已經出棧,即\(a_1,a_2,…,a_{k-1}\)都已經出棧;
\(a_k\) 之后的所有數據項中,小于 \(a_k\)的都在棧內,大于\(a_k\)的尚未入棧;
\(a_k\)之后緊跟的出棧數據項 \(a_{k+1}\) 要么大于\(a_k\),要么是所有未出棧的比\(a_k\)小的數據項中最大的一個
結論 1 很明顯,因為本身就是出棧序列,因此之前的數據肯定已經出棧;結論 2 中,之后的數據只有兩種存在的可能:在棧內,或者未進棧。比\(a_k\)小的如果未進棧,那么 akak 根本不可能出棧(因為就沒進棧),比\(a_k\)大的如果在棧內,那\(a_k\)也無法出棧,因為\(a_k\)在它的下面,因此得證;結論 3,\(a_{k+1}\)就是\(a_k\) 出棧后棧頂的數據,因此必然是在棧內的數據的最上面的一個,或者是棧外的某一個數據(進棧再出棧)。
于是由結論 3 找到判斷序列的方法:逐個檢查序列的每一項\(a_k\),將該項之后的數據分為大于該數據的大數集合\(S_g\)和小于該數的小數集合\(S_l\),查看是否后續的數據項是小數集合的最大值或者是大數集合的任意值,如果不是則不是出棧序列,即若 \(a_{k+1}\in S_g\) 或 \(a_{k+1}=max_l{S_l}\),即是出棧序列。
問題一的解答,就是窮舉長度為 nn 的序列,逐個進行判斷,得到最后的結果,附上 python 程序。
import math
import itertools
% 輸入序列的長度
n = raw_input(“Input n: ”)
% 判斷是否是出棧序列
def IsNotStackSeq(n_ls, n):
for k in range(0,n-2):
% 逐個檢查序列中的每一個元素
ak = n_ls[k]
set_in = n_ls[k+1:]
a_max = ak
% 將ak之后的元素分為大于和小于兩組集合
min_list = [item for item in set_in if item 》 ak]
max_list = [item for item in set_in if item 《 ak]
if len(max_list) 》 0:
a_max = max(max_list)
% 后續的元素是否是小于集合的最大值或者屬于大于集合
if n_ls[k+1] != a_max and (n_ls[k+1] not in min_list):
return 1
return -1
def StackSeqList(n):
n_permation = list(itertools.permutations(range(1,int(n)+1), int(n)))
n_list = [item for item in n_permation if IsNotStackSeq(list(item),int(n)) 《 0]
return (len(n_list),n_list)
編輯:hfy
-
堆棧
+關注
關注
0文章
182瀏覽量
19732 -
數據結構
+關注
關注
3文章
573瀏覽量
40092 -
python
+關注
關注
56文章
4782瀏覽量
84453
發布評論請先 登錄
相關推薦
數據結構的幾個重要知識點
UCOSIII任務堆棧和STM32堆棧增長方向是否一致?
STM32堆棧區劃分
堆和棧有什么區別堆棧的詳細資料說明
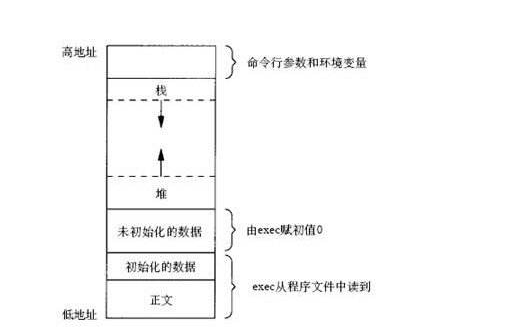
JAVA的堆和棧介紹和內存機制中堆和棧的區別及變量在內存中的分配

什么是棧?數據結構中棧如何實現
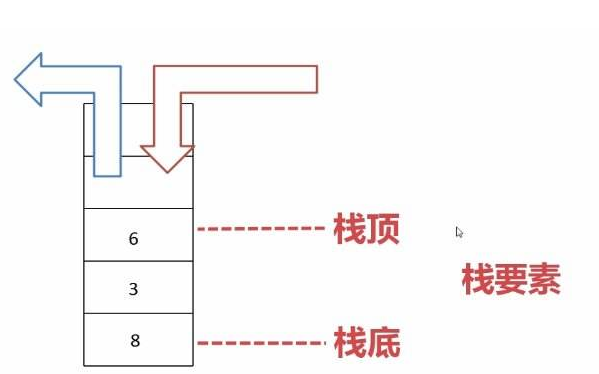




 數據結構中堆棧出棧序列問題解析
數據結構中堆棧出棧序列問題解析











評論