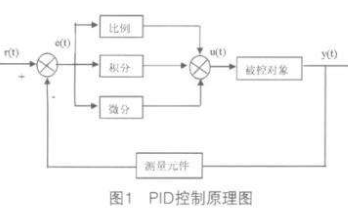
算法原理

PID控制器即比例（proportion）、積分（integral）、微分（differential）控制器， 該算法以誤差作為輸入量，經過對比例，積分，微分三項加權求和之后得到輸出量。PID控制器是非常經典的控制器，簡單易懂，不需要精確的系統模型就可以使用，應用非常廣泛。

關于PID的介紹資料網上有很多，也有很多講的通俗易懂的。

我這里介紹算法原理時除了定性分析之外，還會涉及到一部分理論知識，需要一定的《自動控制原理》和《信號與系統》的專業知識，不過不會過于深入，都是簡單的入門級知識。

我們先說一下為什么需要閉環控制，以控制一個電機的轉速為例。在實際控制之前，我們可能會想當然的覺得，只要我給電機一個100轉/min的轉速期望，它就會乖乖輸出100轉/min的結果，但是實際情況呢？電機空載的情況下它或許還能夠達到期望的轉速，但是假如給電機上加了一個10斤的負載呢？它的轉速可能就掉到80轉/min去了，再繼續增加負載，轉速可能會繼續下降。

再舉一個例子，做過智能小車之類的同學應該會深有體會，單片機輸出同樣脈寬PWM給電機，但是隨著電源電壓，輪子松緊等因素的干擾，幾乎每次電機最后輸出的實際轉速都會變化。

如何解決這個問題呢？其實我們只需要根據電機的實際轉速來改變我們的給電機的輸入量就可以了。比如同樣是希望電機掛了10斤負載的情況下能夠輸出100轉/min，由于給電機的輸入對應于空載100轉/min時，實際輸出只有80轉/min，可以考慮將輸入量提高到對應于空載時120轉/min，這時電機的實際輸出或許就能夠達到100轉/min。同樣的，如果負載繼續增加，我們就進一步增大輸入量，以控制實際輸出保持在100轉/min。

Robomaster的大部分電機都是帶霍爾傳感器，可以反饋轉速/位置信息的，因此都可以通過閉環的方式進行控制。

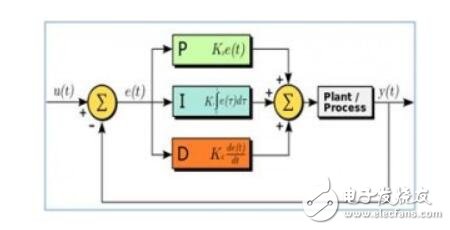
然后我們介紹一下什么是典型的反饋控制器（該模型可以在matlab的simulink中打開）：

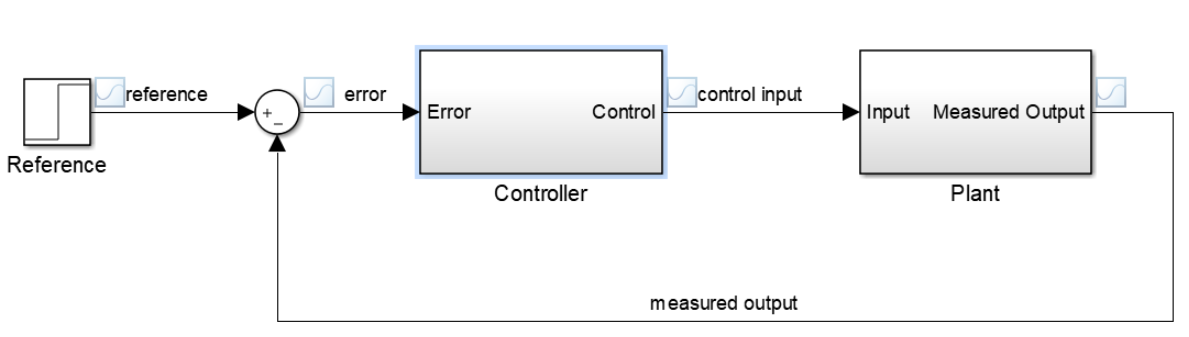
一般我們會將受控對象的反饋（measured output）與我們的期望(reference)輸入相減，得到一個誤差值(error)，然后以該誤差作為輸入量給控制器(controller)，控制器最后輸出結果(control input)直接傳給受控對象(plant)。

依然是結合我們之前的電機的例子，這里的期望即我們的期望電機轉速100轉/min，反饋即我們通過霍爾傳感器獲得的電機實際轉速80轉/min，我們將他們做差得到誤差，然后將其送入控制器中，控制器根據內部的算法得到結果，算出120轉/min的期望給電機，就能夠使電機的實際轉速恰好等于期望。

由于誤差和控制器輸出都是時變的，我們分別假設其為err(t)和U(t)，這樣我們就可以引出連續型PID的公式

U(t)=Kp?err(t)+Ki?∫err(t)dt+Kd?derr(t)dtU(t)=Kp?err(t)+Ki?∫err(t)dt+Kd?derr(t)dt

即對err(t)分別進行比例，積分，微分運算之后進行加權求和得到輸出U(t)。為什么會同時需要這三項呢？我們來定性的分析一下每一項的含義——

首先我們假設Ki和Kd兩個系數均為0，則公式變化為

U(t)=Kp?err(t)U(t)=Kp?err(t)

即輸出量隨誤差大小等比例變化，那么這樣得到的輸出結果會是什么樣的呢？(藍線為輸出，黃線為期望，紫線為誤差)

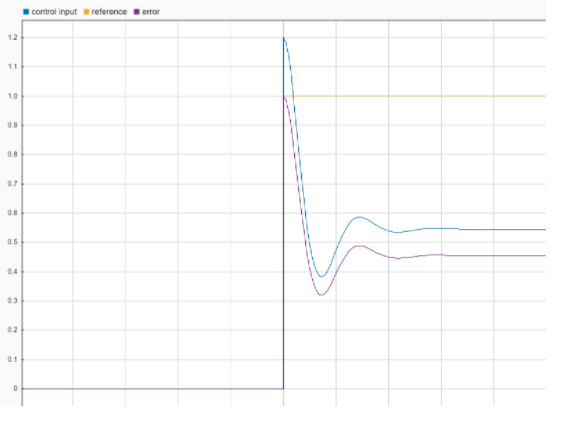
我們會發現輸出出現了兩個問題——第一，出現了超調，第二，出現了靜差。

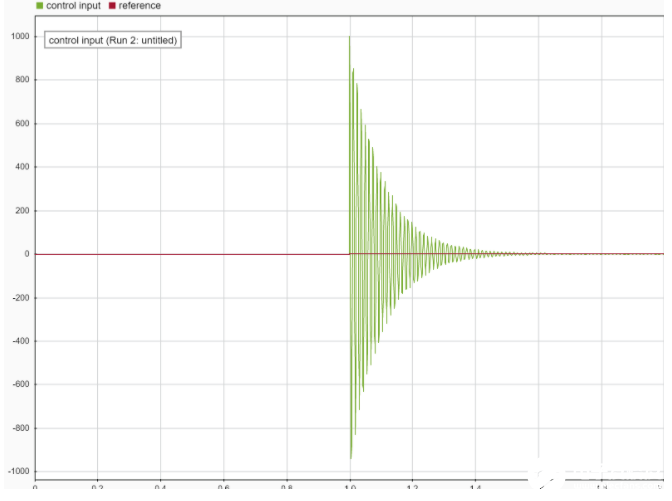
超調即實際輸出量出現了一個大于期望值的尖峰，超調可能會引發很嚴重的問題——系統不穩定，這種情況往往出現在比例項過大的情況。一個超調量引發另一個超調，導致系統處于持續的震蕩狀態中，比如下圖這種情況——

體現在實際的機器人中就會是“嘿，你的云臺瘋了”或者“嘿，你的底盤瘋了”，你會看見自己的機器人的云臺抽風一般的抽搐點頭，底盤如同脫韁的野馬肆意奔馳.......（所以為了安全，一定要給輸出添加限幅！！被云臺打到或者被底盤撞到真的很疼！！）

靜差即輸出穩定在一個小于期望的值，引發這一點的問題之一是比例系數過小。因為我們知道輸出是和誤差成正比例的，如果比例系數小了，則輸出自然也會小。適當的增大比例系數可以改善這一問題，但是永遠不可能徹底消除靜差，因為如果真的達到了輸出等于期望，也就是err(t)等于0的情況，則輸出U(t)就也為0了......我們來看一下增大比例項的結果：靜差大大減小，但是超調也增大了。

所以我們可以看出純比例控制所遇到的一個矛盾的問題，系數太小則存在靜差，系數太大則存在超調，所以為了解決這一問題，我們需要提高系統階數，引入積分項。

引入積分項后，公式變成

U(t)=Kp?err(t)+Ki?∫err(t)dtU(t)=Kp?err(t)+Ki?∫err(t)dt

我們來分析一下積分項是如何解決靜差這個問題的。由于積分的累積性，只要存在誤差，積分項就會持續作用，即使在err(t)為0時，積分項也不會為0，而是繼續保持作用，維持U(t)不為0。但是需要注意的是，積分項對于輸出的影響是比較大的，不能貿然給很大的積分系數，否則......（“嘿，你云臺/底盤瘋了”），此外積分項一定程度上會助長超調的影響，使系統趨于穩定的時間變得更久，如下圖所示。

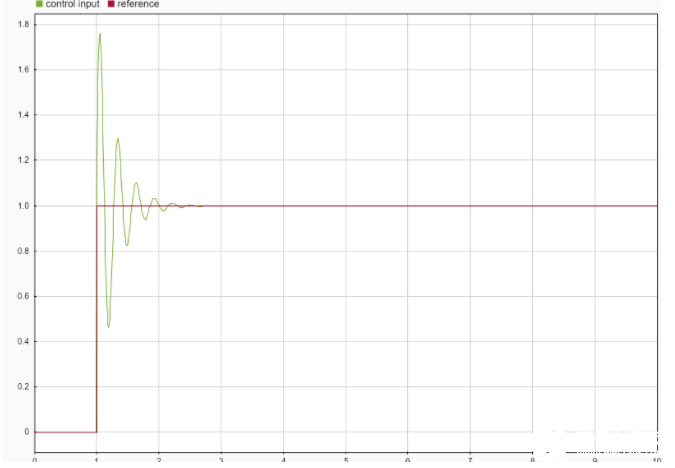
通過增加積分項，我們解決了靜差這一問題，但是超調問題依然存在，雖然通過增加減小比例項和積分項可以一定程度上的減小超調，但是代價就是輸出消除靜差的時間又要被延長了。所以這時我們引入第三項微分項。這時我們就得到了真正的完整PID控制器公式——

U(t)=Kp?err(t)+Ki?∫err(t)dt+Kd?derr(t)dtU(t)=Kp?err(t)+Ki?∫err(t)dt+Kd?derr(t)dt

微分項的意義何在呢？我們可以將其與物理中的阻尼概念聯系起來。每當err(t)產生急劇變化時，就會產生一個很大的微分項來抵消這一急劇的變化。這就恰好和我們的超調現象相對應，因為超調正是一個急劇上升后急劇下降的尖峰，而微分項是來和它做抵消的。

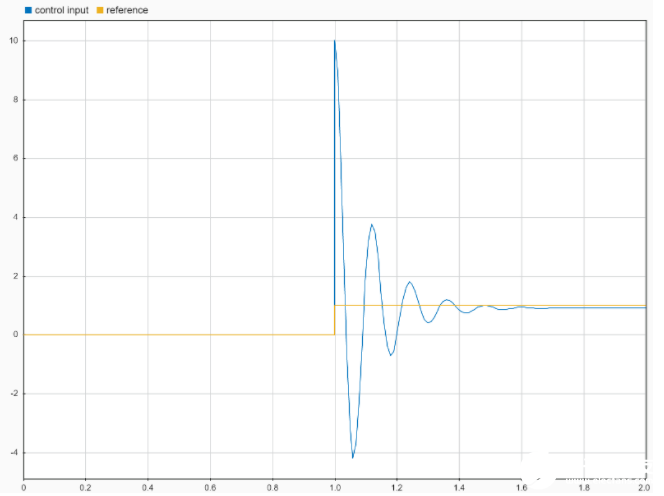
我們來看一下引入微分項后的輸出結果——

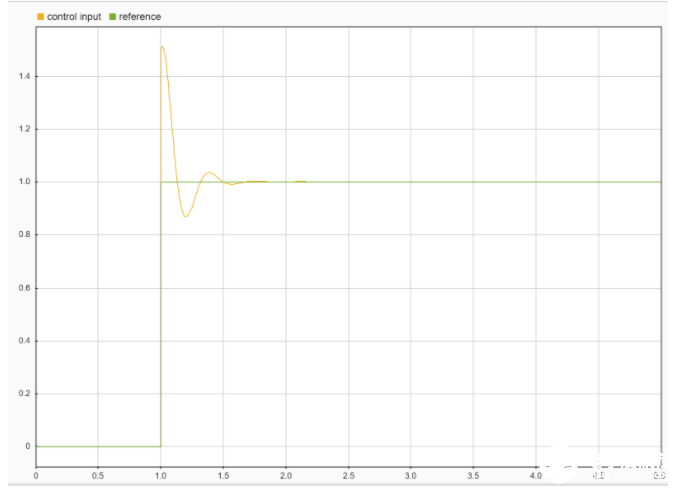
可以看到超調量大大減小，且系統恢復穩定的時間也加快了。

通過以上的分析，我們知道了PID控制器各項的作用。然而注意，上面所說的一切都只是定性分析，下面讓我們來結合《信號與系統》以及《自動控制原理》的專業知識，來說一下PID更深層次的原理，沒有相關基礎的同學可以跳過這一部分。

我們引入傳遞函數來進行系統穩定性的分析，一個閉環控制系統的系統框圖如下——

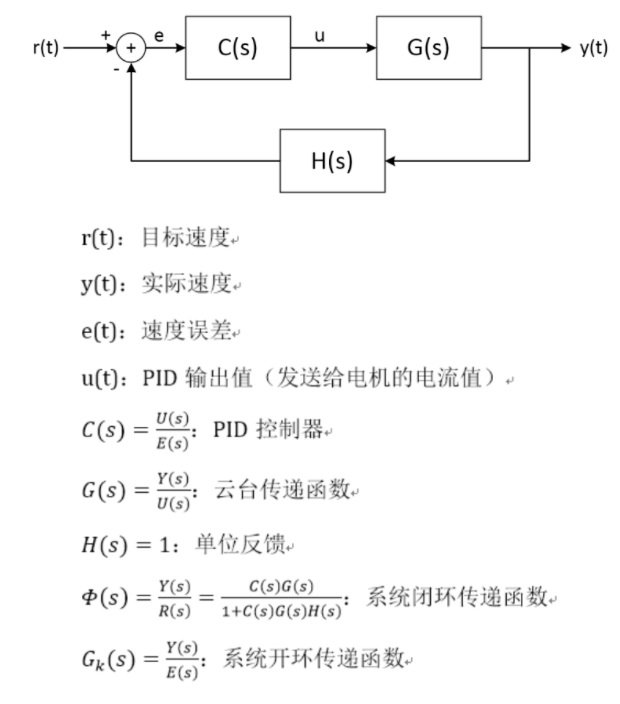
假設我們已經獲得了云臺的傳遞函數（可以通過系統辨識獲得）

寫出PID控制器的s域表達式如下：

U(s)=Kp+Ki?1s+Kd?sU(s)=Kp+Ki?1s+Kd?s

通過調節積分項，使積分段作用于系統的低頻成分，保證系統穩定性，將微分段作用于系統的高頻成分，保證系統的動態性能。

在自動控制原理中，我們知道一個系統穩定的條件是該系統的極點全部位于復平面左側。所以任何控制器所做的首要任務是配置系統極點，舉一個例子。假設一個系統傳遞函數為

G(s)=1s?1G(s)=1s?1

顯然其開環不穩定，其閉環傳函為

Φ(s)=G(s)1+G(s)H(s)=1sΦ(s)=G(s)1+G(s)H(s)=1s

顯然閉環系統極點在原點上，不穩定

而在引入前饋純比例控制器

C(s)=2C(s)=2

之后，我們可以看到閉環傳函變為

Φ(s)=C(s)G(s)1+C(s)G(s)H(s)=2s+1Φ(s)=C(s)G(s)1+C(s)G(s)H(s)=2s+1

系統極點為s=-1，系統穩定。

在保證系統穩定的前提下，我們根據系統閉環傳遞函數的波特圖進行分析，使幅頻響應和相頻響應滿足幅度裕度條件和相位裕度條件，可以借助matlab的工具箱進行分析。

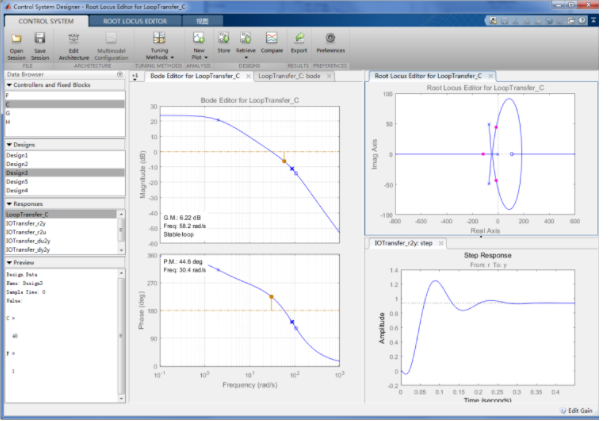
關于系統辨識以及根據系統辨識的結果設計控制器，可以參考官方的開源教程

https://bbs.robomaster.com/thread-4941-1-1.html

https://bbs.robomaster.com/thread-5059-1-1.html

當然，沒有掌握這些知識不代表一個人不能調PID，同樣一個人掌握了這個知識也不等于他一定能夠調好PID，很多情況下系統的傳遞函數并不容易獲取，所以經驗依然非常非常重要。

代碼實現

需要注意的是，前文我們一直在討論連續型PID控制器，但是單片機內部是一個數字系統，數字系統必然是離散的，所以我們需要把連續型PID轉換出離散型PID，當然這一點其實也沒有任何難度，只不過是把積分變成求和，微分變成差分而已。

離散型PID公式如下

U(n)=Kp?err(n)+Ki?∑err(n)+Kd?[err(n)?err(n?1)]U(n)=Kp?err(n)+Ki?∑err(n)+Kd?[err(n)?err(n?1)]

眼尖的同學注意到我沒有把周期T寫在公式里面，其實考慮到周期是一個常數，我把它直接合在了系數中。

這里對應到代碼中，也告訴了我們兩件事

PID控制器的運算必須在定時中斷中執行

采樣周期和控制周期會影響系數

關于第二點特別說明一下，一般來說增加控制周期和采樣周期是可以讓我們的控制變得更加平滑，控制周期即執行控制代碼的周期，一般是放置運算PID代碼的定時器的周期，采樣周期即獲取傳感器數據的周期，比如電機的采樣周期就是CAN接收中斷的周期。

最后我們依然是結合官方開源代碼來理解PID的代碼實現。

這是pid.c下的pid_calculate函數，結合公式可以很容易理解含義。set即期望，get即反饋，兩者相減得到誤差err，pid->pout即比例項，直接將err線性放大，pid->iout即積分項，對err進行累加，pid->dout即微分，對err做差分。最后將三者疊加得到pid控制器輸出。

/**
  * @brief     calculate delta PID and position PID
  * @param[in] pid: control pid struct
  * @param[in] get: measure feedback value
  * @param[in] set: target value
  * @retval    pid calculate output 
  */
float pid_calculate(struct pid *pid, float get, float set)
{
  pid->get = get;
  pid->set = set;
  pid->err = set - get;
  if ((pid->param.input_max_err != 0) && (fabs(pid->err) > pid->param.input_max_err))
    return 0;

  pid->pout = pid->param.p * pid->err;
  pid->iout += pid->param.i * pid->err;
  pid->dout = pid->param.d * (pid->err - pid->last_err);

  abs_limit(&(pid->iout), pid->param.inte_limit);
  pid->out = pid->pout + pid->iout + pid->dout;
  abs_limit(&(pid->out), pid->param.max_out);

  return pid->out;
}

調參技巧

最后說一點關于調參的問題，當然不會具體到各個參數的調節上，因為這個東西往往是各執一詞，不同的人調起PID來即使大思路一致，具體細節上依然可能會有各種各樣的不同。這里更多是推薦一些調參的工具，方法，注意事項等。

首先是工具，這里就要搬出我們無敵的Jscope了，在之前的博文中也提到過，這是一個非常便利的虛擬示波器，在mdk中由于只能看到數值，很難分析系統的動態性能，所以Jscope在這時可以派上大用處——

直接上官網就可以免費下載，建議使用比較新的版本，舊的版本存在不能查看結構體內部變量，不能正常畫浮點數波形等一些問題。

然后是方法，這里說的方法不是說PID的參數調節順序之類的（雖然正常人都是先調P然后I,D），而是如何設計輸入與如何評價輸出。設計輸入時，一般以階躍信號作為輸入，逐步提升階躍幅值以測定系統魯棒性。進一步測試時可以將窄方波脈沖當作沖激信號來輸入，因為賽場上的沖擊一般是被可以看作沖激的，RM這個比賽一定程度上檢驗的就是穩定性，對自己系統的穩定性界限心知肚明對一個電控隊員來說是很重要的。

評價輸出則根據超調量，靜差，恢復時間等參數作為指標。理想的輸出曲線自然是能夠又快又不超調的貼合上期望曲線，然后根據實際情況來調整參數，出現超調時適當衰減比例項，恢復時間過長時適當減小積分項，增大微分項等等。必須在調參的一開始就定好系統的靜態和動態性能指標，有的放矢才能提高效率。

最后是注意事項：記得給控制器的輸出限制幅度，切記，切記，切記，被鐵疙瘩狠狠打一下或者撞一下，輕則瘀傷，重則傷筋動骨，希望各位電控同學注意自己的生命安全。一般調車時我個人不會把車放在地上調，而是放在車架上，這樣可以在一定程度上避免跑飛帶來的危險。

另外可以適當考慮采用無線下載器，磁吸附線等，保護好自己的下載器也是很重要的，在越來越多的隊伍使用滑環做小陀螺的RM賽場上，云臺抽風打轉很有可能直接扯斷下載線......

結語

關于PID就先說這么多了，還是那句話，實踐出真知。掌握PID的理論可以幫助一個人更加科學地去調參，但是光有理論沒有實踐是沒有意義的，還是得多調，積累經驗才行。
編輯：hfy