作者：Charles Hymowitz

工程師們進行蒙特卡羅分析并評估其結(jié)果的方式有可能是不正確的，錯誤理解蒙特卡羅分析結(jié)果可能導致不正確的技術(shù)和商業(yè)決策。在電路蒙特卡羅分析中，分析人員設(shè)定了會影響結(jié)果的每個元件特性的概率，并運行多電路仿真來找出給定函數(shù)的各種可能的結(jié)果。

這可能會讓人感到意外，但工程師們進行蒙特卡羅分析并評估其結(jié)果的方式有可能是不正確的。錯誤理解蒙特卡羅分析結(jié)果可能導致不正確的技術(shù)和商業(yè)決策。當然，蒙特卡羅分析法是有幫助的，實際上有多種蒙特卡羅分析方法可以使用，你感到驚訝嗎？

蒙特卡羅分析法是一種多變量建模技術(shù)，你可以將其視為一系列的“假設(shè)”場景。它允許工程師進行多次實驗，并對一組給定結(jié)果定義概率分布或完成風險評估。在電路蒙特卡羅分析中，分析人員設(shè)定了會影響結(jié)果的每個元件特性的概率（一些元件具有很多不同的特性），并運行多個電路仿真來找出給定函數(shù)的各種可能的結(jié)果。

許多電路函數(shù)的參數(shù)變化不是單調(diào)的。因此，蒙特卡羅分析對于最壞情況電路分析（WCCA）很重要。僅進行極值分析（EVA）評估是不夠的，因為這會使許多分析不產(chǎn)生最壞的結(jié)果。最壞的情況往往不是在參數(shù)極端的情況下產(chǎn)生的，所以如果只做EVA，會錯過某些情況。

關(guān)于分析的順序存在許多錯誤觀念和錯誤的WCCA指南。要使用哪種分析方法取決于幾個因素，其中包括待評估函數(shù)的參數(shù)容差是否單調(diào)變化。

分析的順序并不一定是極值分析（EVA）、統(tǒng)計平方公差（RSS）和蒙特卡羅分析，即使這是許多指南所給出的順序。實際上，并沒有正式的“分析順序”。容差和分析方法基本上是相互獨立的，RSS容差可以應(yīng)用于靈敏度、參數(shù)EVA或蒙特卡羅分析方法。盡管極值分析可以是有價值的第一步，通常可以讓你了解哪些參數(shù)對輸出函數(shù)有最大影響，但它并不一定是第一或唯一使用的方法。

如果一個分析結(jié)果不合規(guī)，不要將蒙特卡洛分析視為“后備”。在許多情況下，降低保守性當然是有用的，但這不是最壞情況分析（為什么要進行最壞情況分析，請參見另一篇文章，《Why worst-case circuit analysis is challenging to perform》。對于許多類型的分析，包括穩(wěn)定性和總線/階躍負載瞬態(tài)分析，或者分析哪里存在大量參數(shù)容差，蒙特卡羅才是首選，也許是唯一需要完成的分析。

另一個誤解是蒙特卡洛分析需要完成大量的實驗。這不一定是對的。

蒙特卡洛分析示例

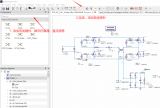
圖1顯示了一個使用狀態(tài)空間平均模型的蒙特卡羅分析示例，用來分析一個開關(guān)電源的穩(wěn)定性。仿真運行AC分析，看控制回路是否符合普遍接受的10dB增益裕度（頂部曲線）、30°相位裕度（中心曲線）的航天工業(yè)指南。圖中還顯示了與不穩(wěn)定奇點（-1,0）（底部圖）的距離。

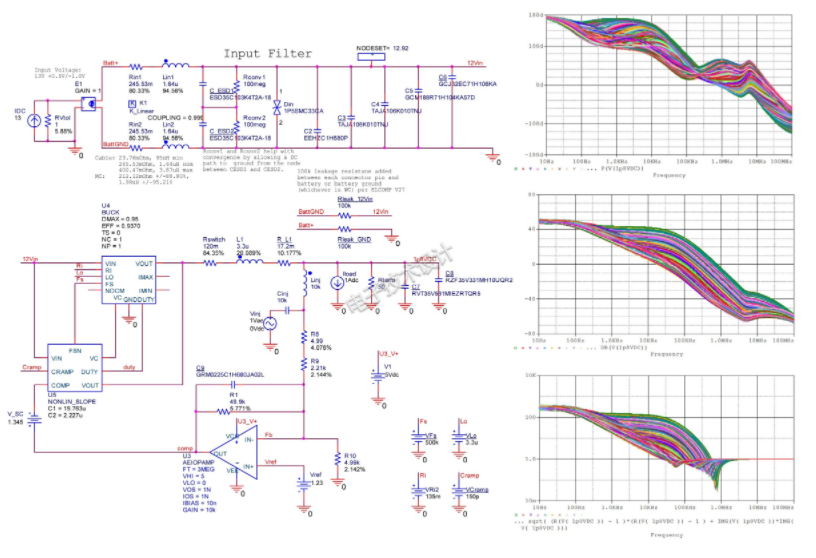
圖1：開關(guān)電源的蒙特卡羅分析顯示了（從上到下）增益裕度、相位裕度以及與不穩(wěn)定奇點的距離。

在這個例子中，我們?yōu)橛绊懘治鲚敵龊瘮?shù)的每個元件指定了一個容差范圍和分布——通常是高斯分布或均勻分布。然后仿真一些（非任意）情況，其中容差特性根據(jù)它們的分布而變化，并把待分析輸出函數(shù)的結(jié)果記錄下來。

我們記錄了對圖1中12V~1.8V穩(wěn)壓器進行AC穩(wěn)定性分析期間在到不穩(wěn)定奇點的距離上得到的增益、相位和穩(wěn)定性裕度。記錄每個輸出函數(shù)的統(tǒng)計數(shù)據(jù)（平均值和標準偏差）和最壞情況（終點）。若只做穩(wěn)定性分析，從圖2顯示的穩(wěn)定性裕度可以看出其性能。

圖2：穩(wěn)定性示例結(jié)果通常僅涉及相位和增益裕度。然而，穩(wěn)定性裕度可以更好更準確地評估穩(wěn)定性。為了方便起見，將與不穩(wěn)定奇點的距離轉(zhuǎn)換為度數(shù)，并與30°需求進行比較。

蒙特卡羅結(jié)果必須在有效的統(tǒng)計框架中進行評估。該框架包括一個置信區(qū)間以及一個與具體實例相關(guān)的置信水平（或確定性）組合。沒有此框架，就無法正確評估結(jié)果。

一個函數(shù)的容差區(qū)間基于總體的測量樣本，是一個存在某種可能性（或者感覺到某種程度的置信度）的區(qū)間，這種可能性就是總體的指定部分的值。

使用任意次運行后的最大和最小結(jié)果作為“最壞情況”，并不是執(zhí)行和評估蒙特卡羅分析的正確方法。這是因為，從統(tǒng)計學角度來說，你并不知道計算了什么樣的性能范圍。例如，不應(yīng)該只完成500次（或100或1000次等）實驗，并為了滿足規(guī)范要求而將終點作為“最壞情況”結(jié)果。以這種方式完成的蒙特卡羅分析很容易導致不正確的設(shè)計決策，因為結(jié)果有可能比預(yù)期更差，也有可能比預(yù)期更好。

對于航空航天和汽車領(lǐng)域的WCCA，可以使用以下兩種方法中的一種來執(zhí)行蒙特卡羅分析：正態(tài)分布容差區(qū)間法，其結(jié)果是平均值±幾個西格瑪；或與分布無關(guān)的容差區(qū)間法（非參數(shù)統(tǒng)計），其結(jié)果是最壞情況結(jié)果。在這兩種情況下，運行次數(shù)都與具體的確定性和總體覆蓋率相關(guān)聯(lián)。

對終點值的使用是有特殊規(guī)則的。根據(jù)所選擇的蒙特卡羅方法，結(jié)果的分布情況有可能重要，也可能并不重要。在圖2的情況下（穩(wěn)定性裕度直方圖），結(jié)果不是正態(tài)分布。因此，應(yīng)該使用與分布無關(guān)的方法。

對于正態(tài)分布容差區(qū)間法，被仿真的函數(shù)（穩(wěn)定性，階躍負載，紋波等）的平均值和標準偏差是根據(jù)蒙特卡羅結(jié)果計算得出的。然后使用范圍（平均值±幾個σ）計算性能，其中西格瑪?shù)膫€數(shù)基于總體（概率）覆蓋率/置信水平（確定性），通常為99.73％/99％，99.73％/95％，或99％/90％。航空航天讀者可能會看出99/90與用于小樣本輻射評估的統(tǒng)計數(shù)據(jù)相同。要使蒙特卡洛評估有效，這兩個數(shù)都必須定義，因為我們是在處理采樣數(shù)據(jù)系統(tǒng)。必須遵循“3σ”準則進行分析這種說法是不全面的。

置信水平

我們可以使用免費的在線工具來計算概率置信水平組合，表1對50個案例進行了蒙特卡羅分析，顯示了容差區(qū)間計算的結(jié)果。這個免費的Excel/在線工具可以設(shè)定總體覆蓋率和確定性的案例個數(shù)，確定標準偏差的正確個數(shù)。這里顯示了一個常用組合——50例，±4（3.942）σ，相當于99.73％/99％。輸出函數(shù)的分布必須是高斯分布。

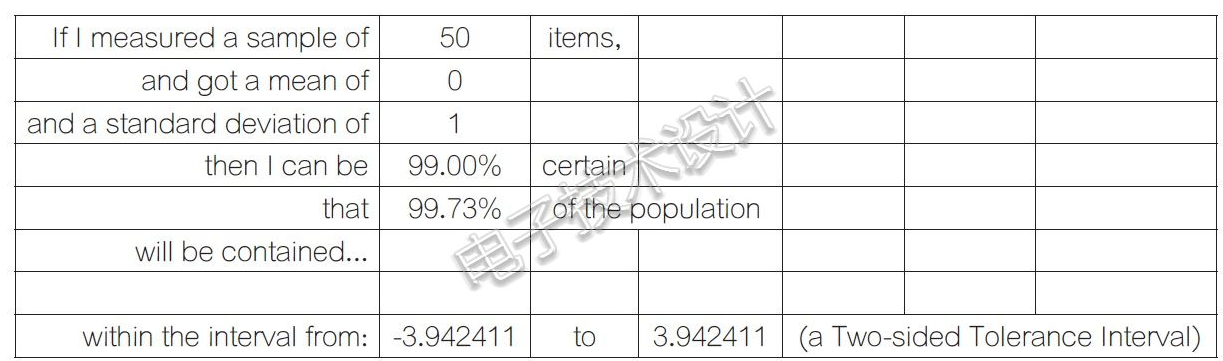
表1：50個例子的容差區(qū)間——99.73/99≈4σ，99/90≈3σ。

置信水平和總體覆蓋率互為反比。因此，給定相同的西格瑪數(shù)量可以表示無限數(shù)量的置信度/總體覆蓋率組合。對于99.9％的置信水平，總體覆蓋率為99.315％，例如，使用30個例子，其中均值=0，標準差=1。

在線Excel計算器根據(jù)有限樣本的均值和標準差，在假設(shè)最后的總體是正態(tài)分布（高斯）的情況下，計算出給定總體比例和任何指定置信水平的容差區(qū)間。在該示例中，99.73％/99％相當于大約4σ，99％/90％相當于3σ。

50個例子是隨便選的。運行的例子數(shù)量可以是任意的，對于選定的置信區(qū)間/總體覆蓋率，將產(chǎn)生特定數(shù)量的標準差。但50是一個比較實際的數(shù)字，它不會因為太大而在SPICE仿真過程中遇到收斂問題，也不會因太小而引起不熟悉這種方法的評審人的質(zhì)疑。對于最常選擇的置信區(qū)間和總體覆蓋率，它也恰好產(chǎn)生西格瑪約整數(shù)。

如上所述，對于正態(tài)分布容差區(qū)間法，最壞情況性能不是最大和最小終點仿真結(jié)果，而是平均值加上或減去指定的標準偏差數(shù)。

正態(tài)分布容差區(qū)間法的關(guān)鍵在于它只有在輸出函數(shù)結(jié)果的分布是正態(tài)或非常接近正態(tài)（例如不是偏態(tài)的）時才有效。正態(tài)性是可以測試的。如果分布是非正態(tài)的，則應(yīng)該使用與分布無關(guān)的容差區(qū)間法，因為輸出變量總體的去偏是一個很具挑戰(zhàn)的數(shù)學過程。

底層元件容差分布和輸出函數(shù)的靈敏度會極大地影響輸出函數(shù)的分布。例如，控制回路穩(wěn)定性通常高度依賴等效串聯(lián)電阻（ESR），其變化可達數(shù)量級。當ESR接近其最小值或規(guī)范最大值時，穩(wěn)定性的仿真結(jié)果可能會高度偏斜。

因此，蒙特卡羅穩(wěn)定性分析通常通過與分布無關(guān)的方法完成。均勻容差（分布平坦但被截斷）可以得出與高斯分布不同的結(jié)果（假定高斯具有無限概率尾）。顯然，如果已經(jīng)知道元件的容差分布，盡管這種情況很少發(fā)生，就應(yīng)采用它們。

在給定確定性和總體覆蓋率時，與分布無關(guān)的容差區(qū)間法提供了一種基礎(chǔ)，來選擇作為最差情況結(jié)果的仿真終點運行次數(shù)。與正態(tài)分布的容差區(qū)間不同，與分布無關(guān)指的是輸出函數(shù)的分布形態(tài)不會影響結(jié)果。然而，底層容差將影響結(jié)果，并且均勻概率分布將產(chǎn)生與高斯元件容差分布不同的結(jié)果（倒不一定更差）。

圖3中的曲線由R統(tǒng)計軟件包（distfree.cr）生成，它顯示了與分布無關(guān)的置信水平的適當運行次數(shù)。“與分布無關(guān)”意味著輸出結(jié)果的分布不必是高斯分布。使用指定的概率和確定性，將表現(xiàn)最差的情況（終點）視為性能范圍。

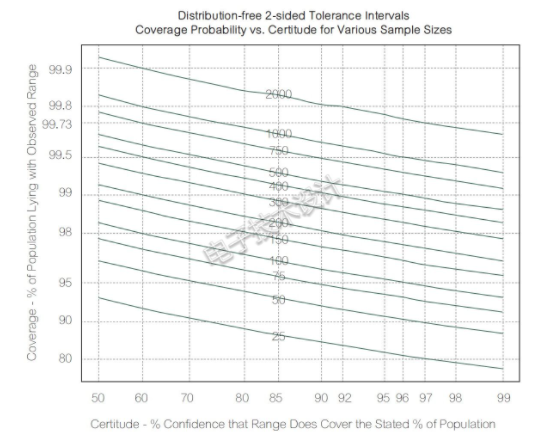
圖3：構(gòu)建與分布無關(guān)的雙側(cè)容差區(qū)間所需的最小樣本量。蒙特卡羅運行數(shù)量隨總體覆蓋率和確定性而變化。

表2顯示了使用99.73％/90％總體覆蓋率/確定性對最差情況范圍的計算，運行次數(shù)必須為1440。最差性能結(jié)果定義了范圍。

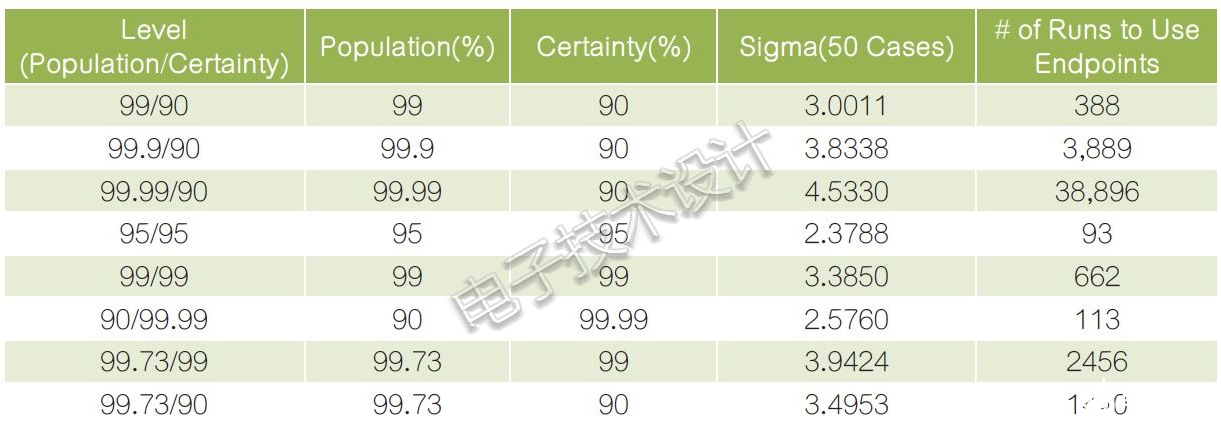
表2：常用的與分布無關(guān)的蒙特卡羅運行計數(shù)和標準偏差范圍，與總體覆蓋率和確定性的關(guān)系。

那么，什么是正確的總體覆蓋率和確定性呢？這通常取決于應(yīng)用、程序以及待評估的給定函數(shù)的性能期望水平。

結(jié)語

最差情況分析是一項很具挑戰(zhàn)的工作，它需要許多的專業(yè)知識。獲得結(jié)果的最佳方法并不總是顯而易見的。如果沒有選擇或使用正確的方法，就可能浪費大量時間并且結(jié)果還不正確。對于輸出與所有底層容差變量不是單調(diào)關(guān)系的任何評估，蒙特卡羅分析幾乎是必不可少的。通常，單調(diào)性是未知的。如果執(zhí)行蒙特卡洛分析，則必須定義總體覆蓋率和確定性以正確評估結(jié)果。無論是使用正態(tài)分布容差區(qū)間法還是與分布無關(guān)的容差區(qū)間法，都是如此。
編輯：hfy