機器學習中的監督學習本質上是給定一系列訓練樣本，嘗試學習的映射關系，使得給定一個，即便這個不在訓練樣本中，也能夠得到盡量接近真實的輸出。而損失函數（Loss Function）則是這個過程中關鍵的一個組成部分，用來衡量模型的輸出與真實的之間的差距，給模型的優化指明方向。

本文將介紹機器學習、深度學習中分類與回歸常用的幾種損失函數，包括均方差損失 Mean Squared Loss、平均絕對誤差損失 Mean Absolute Error Loss、Huber Loss、分位數損失 Quantile Loss、交叉熵損失函數 Cross Entropy Loss、Hinge 損失 Hinge Loss。主要介紹各種損失函數的基本形式、原理、特點等方面。

目錄

前言

均方差損失 Mean Squared Error Loss

平均絕對誤差損失 Mean Absolute Error Loss

Huber Loss

分位數損失 Quantile Loss

交叉熵損失 Cross Entropy Loss

合頁損失 Hinge Loss

總結

前言

在正文開始之前，先說下關于 Loss Function、Cost Function 和 Objective Function 的區別和聯系。在機器學習的語境下這三個術語經常被交叉使用。

- 損失函數 Loss Function 通常是針對單個訓練樣本而言，給定一個模型輸出和一個真實，損失函數輸出一個實值損失

- 代價函數 Cost Function 通常是針對整個訓練集（或者在使用 mini-batch gradient descent 時一個 mini-batch）的總損失

- 目標函數 Objective Function 是一個更通用的術語，表示任意希望被優化的函數，用于機器學習領域和非機器學習領域（比如運籌優化）

一句話總結三者的關系就是：A loss function is a part of a cost function which is a type of an objective function.

由于損失函數和代價函數只是在針對樣本集上有區別，因此在本文中統一使用了損失函數這個術語，但下文的相關公式實際上采用的是代價函數 Cost Function 的形式，請讀者自行留意。

均方差損失 Mean Squared Error Loss

基本形式與原理

均方差 Mean Squared Error (MSE) 損失是機器學習、深度學習回歸任務中最常用的一種損失函數，也稱為 L2 Loss。其基本形式如下

從直覺上理解均方差損失，這個損失函數的最小值為 0（當預測等于真實值時），最大值為無窮大。下圖是對于真實值，不同的預測值的均方差損失的變化圖。橫軸是不同的預測值，縱軸是均方差損失，可以看到隨著預測與真實值絕對誤差的增加，均方差損失呈二次方地增加。

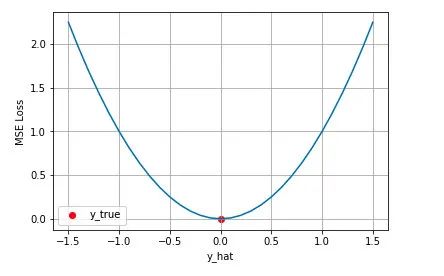
背后的假設

實際上在一定的假設下，我們可以使用最大化似然得到均方差損失的形式。假設模型預測與真實值之間的誤差服從標準高斯分布（），則給定一個模型輸出真實值的概率為

進一步我們假設數據集中 N 個樣本點之間相互獨立，則給定所有輸出所有真實值的概率，即似然 Likelihood，為所有的累乘

通常為了計算方便，我們通常最大化對數似然 Log-Likelihood

去掉與無關的第一項，然后轉化為最小化負對數似然 Negative Log-Likelihood

可以看到這個實際上就是均方差損失的形式。也就是說在模型輸出與真實值的誤差服從高斯分布的假設下，最小化均方差損失函數與極大似然估計本質上是一致的，因此在這個假設能被滿足的場景中（比如回歸），均方差損失是一個很好的損失函數選擇；當這個假設沒能被滿足的場景中（比如分類），均方差損失不是一個好的選擇。

平均絕對誤差損失 Mean Absolute Error Loss

基本形式與原理

平均絕對誤差 Mean Absolute Error (MAE) 是另一類常用的損失函數，也稱為 L1 Loss。其基本形式如下

同樣的我們可以對這個損失函數進行可視化如下圖，MAE 損失的最小值為 0（當預測等于真實值時），最大值為無窮大。可以看到隨著預測與真實值絕對誤差的增加，MAE 損失呈線性增長

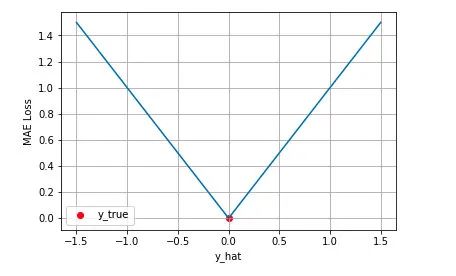
背后的假設

同樣的我們可以在一定的假設下通過最大化似然得到 MAE 損失的形式，假設模型預測與真實值之間的誤差服從拉普拉斯分布 Laplace distribution（），則給定一個模型輸出真實值的概率為

與上面推導 MSE 時類似，我們可以得到的負對數似然實際上就是 MAE 損失的形式

MAE 與 MSE 區別

MAE 和 MSE 作為損失函數的主要區別是：MSE 損失相比 MAE 通常可以更快地收斂，但 MAE 損失對于 outlier 更加健壯，即更加不易受到 outlier 影響。

MSE 通常比 MAE 可以更快地收斂。當使用梯度下降算法時，MSE 損失的梯度為，而 MAE 損失的梯度為，即 MSE 的梯度的 scale 會隨誤差大小變化，而 MAE 的梯度的 scale 則一直保持為 1，即便在絕對誤差很小的時候 MAE 的梯度 scale 也同樣為 1，這實際上是非常不利于模型的訓練的。當然你可以通過在訓練過程中動態調整學習率緩解這個問題，但是總的來說，損失函數梯度之間的差異導致了 MSE 在大部分時候比 MAE 收斂地更快。這個也是 MSE 更為流行的原因。

MAE 對于 outlier 更加 robust。我們可以從兩個角度來理解這一點：

第一個角度是直觀地理解，下圖是 MAE 和 MSE 損失畫到同一張圖里面，由于MAE 損失與絕對誤差之間是線性關系，MSE 損失與誤差是平方關系，當誤差非常大的時候，MSE 損失會遠遠大于 MAE 損失。因此當數據中出現一個誤差非常大的 outlier 時，MSE 會產生一個非常大的損失，對模型的訓練會產生較大的影響。

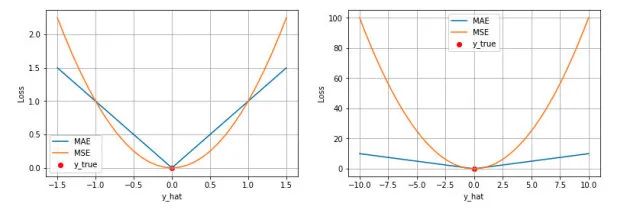
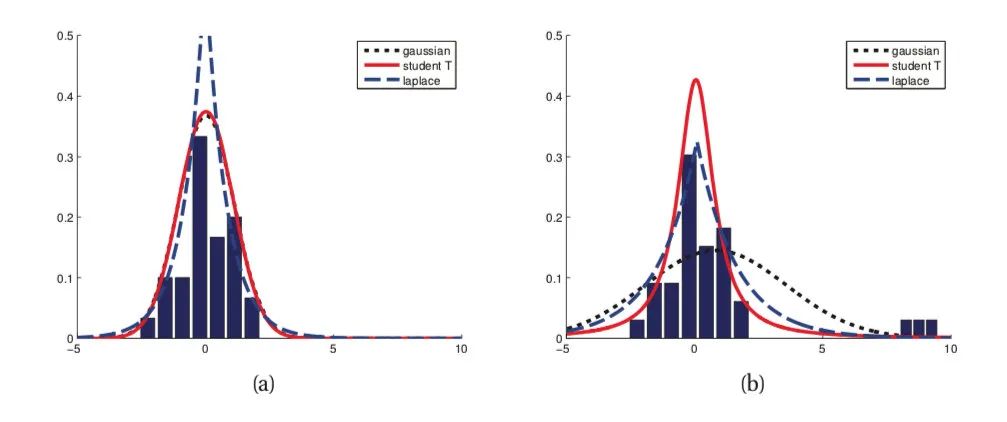
第二個角度是從兩個損失函數的假設出發，MSE 假設了誤差服從高斯分布，MAE 假設了誤差服從拉普拉斯分布。拉普拉斯分布本身對于 outlier 更加 robust。參考下圖（來源：Machine Learning: A Probabilistic Perspective 2.4.3 The Laplace distribution Figure 2.8），當右圖右側出現了 outliers 時，拉普拉斯分布相比高斯分布受到的影響要小很多。因此以拉普拉斯分布為假設的 MAE 對 outlier 比高斯分布為假設的 MSE 更加 robust。

Huber Loss

上文我們分別介紹了 MSE 和 MAE 損失以及各自的優缺點，MSE 損失收斂快但容易受 outlier 影響，MAE 對 outlier 更加健壯但是收斂慢，Huber Loss 則是一種將 MSE 與 MAE 結合起來，取兩者優點的損失函數，也被稱作 Smooth Mean Absolute Error Loss 。其原理很簡單，就是在誤差接近 0 時使用 MSE，誤差較大時使用 MAE，公式為

上式中是 Huber Loss 的一個超參數，的值是 MSE 和 MAE 兩個損失連接的位置。上式等號右邊第一項是 MSE 的部分，第二項是 MAE 部分，在 MAE 的部分公式為是為了保證誤差時 MAE 和 MSE 的取值一致，進而保證 Huber Loss 損失連續可導。

下圖是時的 Huber Loss，可以看到在的區間內實際上就是 MSE 損失，在和區間內為 MAE損失。

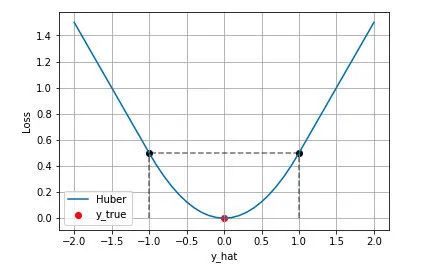
Huber Loss 的特點

Huber Loss 結合了 MSE 和 MAE 損失，在誤差接近 0 時使用 MSE，使損失函數可導并且梯度更加穩定；在誤差較大時使用 MAE 可以降低 outlier 的影響，使訓練對 outlier 更加健壯。缺點是需要額外地設置一個超參數。

分位數損失 Quantile Loss

分位數回歸 Quantile Regression 是一類在實際應用中非常有用的回歸算法，通常的回歸算法是擬合目標值的期望或者中位數，而分位數回歸可以通過給定不同的分位點，擬合目標值的不同分位數。例如我們可以分別擬合出多個分位點，得到一個置信區間，如下圖所示（圖片來自筆者的一個分位數回歸代碼 demo Quantile Regression Demo）

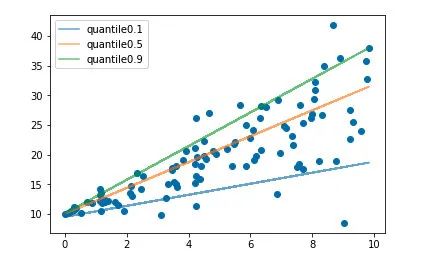
分位數回歸是通過使用分位數損失 Quantile Loss 來實現這一點的，分位數損失形式如下，式中的 r 分位數系數。

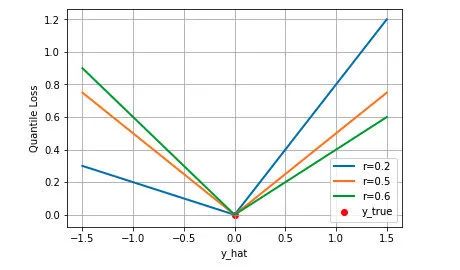
我們如何理解這個損失函數呢？這個損失函數是一個分段的函數 ，將（高估） 和（低估） 兩種情況分開來，并分別給予不同的系數。當時，低估的損失要比高估的損失更大，反過來當時，高估的損失比低估的損失大；分位數損失實現了分別用不同的系數控制高估和低估的損失，進而實現分位數回歸。特別地，當時，分位數損失退化為 MAE 損失，從這里可以看出 MAE 損失實際上是分位數損失的一個特例 — 中位數回歸（這也可以解釋為什么 MAE 損失對 outlier 更魯棒：MSE 回歸期望值，MAE 回歸中位數，通常 outlier 對中位數的影響比對期望值的影響小）。

下圖是取不同的分位點 0.2、0.5、0.6 得到的三個不同的分位損失函數的可視化，可以看到 0.2 和 0.6 在高估和低估兩種情況下損失是不同的，而 0.5 實際上就是 MAE。

交叉熵損失 Cross Entropy Loss

上文介紹的幾種損失函數都是適用于回歸問題損失函數，對于分類問題，最常用的損失函數是交叉熵損失函數 Cross Entropy Loss。

二分類

考慮二分類，在二分類中我們通常使用 Sigmoid 函數將模型的輸出壓縮到 (0, 1) 區間內，用來代表給定輸入，模型判斷為正類的概率。由于只有正負兩類，因此同時也得到了負類的概率。

將兩條式子合并成一條

假設數據點之間獨立同分布，則似然可以表示為

對似然取對數，然后加負號變成最小化負對數似然，即為交叉熵損失函數的形式

下圖是對二分類的交叉熵損失函數的可視化，藍線是目標值為 0 時輸出不同輸出的損失，黃線是目標值為 1 時的損失。可以看到約接近目標值損失越小，隨著誤差變差，損失呈指數增長。

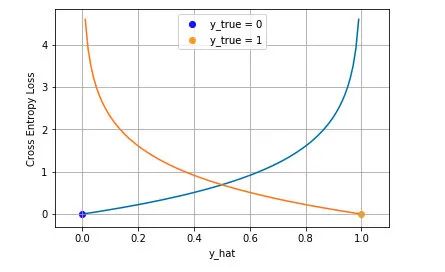
多分類

在多分類的任務中，交叉熵損失函數的推導思路和二分類是一樣的，變化的地方是真實值現在是一個 One-hot 向量，同時模型輸出的壓縮由原來的 Sigmoid 函數換成 Softmax 函數。Softmax 函數將每個維度的輸出范圍都限定在之間，同時所有維度的輸出和為 1，用于表示一個概率分布。

其中表示 K 個類別中的一類，同樣的假設數據點之間獨立同分布，可得到負對數似然為

由于是一個 one-hot 向量，除了目標類為 1 之外其他類別上的輸出都為 0，因此上式也可以寫為

其中是樣本的目標類。通常這個應用于多分類的交叉熵損失函數也被稱為 Softmax Loss 或者 Categorical Cross Entropy Loss。

Cross Entropy is good. But WHY？

分類中為什么不用均方差損失？上文在介紹均方差損失的時候講到實際上均方差損失假設了誤差服從高斯分布，在分類任務下這個假設沒辦法被滿足，因此效果會很差。為什么是交叉熵損失呢？有兩個角度可以解釋這個事情，一個角度從最大似然的角度，也就是我們上面的推導；另一個角度是可以用信息論來解釋交叉熵損失：

假設對于樣本存在一個最優分布真實地表明了這個樣本屬于各個類別的概率，那么我們希望模型的輸出盡可能地逼近這個最優分布，在信息論中，我們可以使用 KL 散度 Kullback–Leibler Divergence 來衡量兩個分布的相似性。給定分布和分布， 兩者的 KL 散度公式如下

其中第一項為分布的信息熵，第二項為分布和的交叉熵。將最優分布和輸出分布帶入和得到

由于我們希望兩個分布盡量相近，因此我們最小化 KL 散度。同時由于上式第一項信息熵僅與最優分布本身相關，因此我們在最小化的過程中可以忽略掉，變成最小化

我們并不知道最優分布，但訓練數據里面的目標值可以看做是的一個近似分布

這個是針對單個訓練樣本的損失函數，如果考慮整個數據集，則

可以看到通過最小化交叉熵的角度推導出來的結果和使用最大 化似然得到的結果是一致的。

合頁損失 Hinge Loss

合頁損失 Hinge Loss 是另外一種二分類損失函數，適用于 maximum-margin 的分類，支持向量機 Support Vector Machine (SVM) 模型的損失函數本質上就是 Hinge Loss + L2 正則化。合頁損失的公式如下

下圖是為正類， 即時，不同輸出的合頁損失示意圖

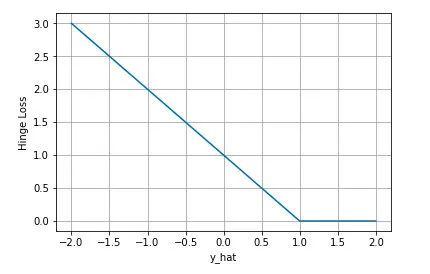
可以看到當為正類時，模型輸出負值會有較大的懲罰，當模型輸出為正值且在區間時還會有一個較小的懲罰。即合頁損失不僅懲罰預測錯的，并且對于預測對了但是置信度不高的也會給一個懲罰，只有置信度高的才會有零損失。使用合頁損失直覺上理解是要找到一個決策邊界，使得所有數據點被這個邊界正確地、高置信地被分類。

總結

本文針對機器學習中最常用的幾種損失函數進行相關介紹，首先是適用于回歸的均方差損失 Mean Squared Loss、平均絕對誤差損失 Mean Absolute Error Loss，兩者的區別以及兩者相結合得到的 Huber Loss，接著是應用于分位數回歸的分位數損失 Quantile Loss，表明了平均絕對誤差損失實際上是分位數損失的一種特例，在分類場景下，本文討論了最常用的交叉熵損失函數 Cross Entropy Loss，包括二分類和多分類下的形式，并從信息論的角度解釋了交叉熵損失函數，最后簡單介紹了應用于 SVM 中的 Hinge 損失 Hinge Loss。本文相關的可視化代碼在 這里。

受限于時間，本文還有其他許多損失函數沒有提及，比如應用于 Adaboost 模型中的指數損失 Exponential Loss，0-1 損失函數等。另外通常在損失函數中還會有正則項（L1/L2 正則），這些正則項作為損失函數的一部分，通過約束參數的絕對值大小以及增加參數稀疏性來降低模型的復雜度，防止模型過擬合，這部分內容在本文中也沒有詳細展開。讀者有興趣可以查閱相關的資料進一步了解。That’s all. Thanks for reading.

責任編輯：YYX