讀完本文，你可以去力扣解決：410.分割數(shù)組的最大值（Hard）

經(jīng)常有讀者問我，讀了之前的爆文二分查找框架詳解之后，二分查找的算法他寫的很溜了，但僅僅局限于在數(shù)組中搜索元素，不知道底怎么在算法題里面運用二分查找技巧來優(yōu)化效率。

那我先說結(jié)論，你想用二分查找技巧優(yōu)化算法，首先要把 for 循環(huán)形式的暴力算法寫出來，如果算法中存在如下形式的 for 循環(huán)：

//func(i)是i的單調(diào)函數(shù)（遞增遞減都可以） intfunc(inti); //形如這種for循環(huán)可以用二分查找技巧優(yōu)化效率 for(inti=0;i

如果func(i)函數(shù)是在i上單調(diào)的函數(shù)，一定可以使用二分查找技巧優(yōu)化 for 循環(huán)。

「在i上單調(diào)的函數(shù)」是指func(i)的返回值隨著i的增加而增加，或者隨著i的增加而減小。

為什么滿足這個條件就可以使用二分查找？因為這個邏輯和「在有序數(shù)組中查找一個元素」是完全一樣的呀！

在有序數(shù)組nums中查找某一個數(shù)target，是不是最簡單二分查找形式？我們看下普通的 for 循環(huán)遍歷算法：

//nums是一個有序數(shù)組 int[]nums; //target是要搜索的元素 inttarget; //搜索target在nums中的索引 for(inti=0;i

既然nums是有序數(shù)組，你把nums[i]看做函數(shù)調(diào)用，是不是可以理解為nums在參數(shù)i上是單調(diào)的？這是不是和之前說的func(i)函數(shù)完全一樣？

當然，前文二分查找框架詳解說過，二分查找算法還有搜索左側(cè)、右側(cè)邊界的變體，怎么運用到具體算法問題中呢？

還是注意觀察 for 循環(huán)形式，只是不一定是func(i) == target作為終止條件，可能是<=或者>=的關系，這個可以根據(jù)具體的題目意思來推斷，我們實操一下力扣第 410 題「分割數(shù)組的最大值」，難度Hard：

函數(shù)簽名如下：

intsplitArray(int[]nums,intm);

這個題目有點類似前文一道經(jīng)典動態(tài)規(guī)劃題目高樓扔雞蛋，題目比較繞，又是最大值又是最小值的。

簡單說，給你輸入一個數(shù)組nums和數(shù)字m，你要把nums分割成m個子數(shù)組。

肯定有不止一種分割方法，每種分割方法都會把nums分成m個子數(shù)組，這m個子數(shù)組中肯定有一個和最大的子數(shù)組對吧。

我們想要找一個分割方法，該方法分割出的最大子數(shù)組和是所有方法中最大子數(shù)組和最小的。

請你的算法返回這個分割方法對應的最大子數(shù)組和。

我滴媽呀，這個題目看了就覺得 Hard，完全沒思路，這題怎么能和二分查找算法扯上關系？

說個小插曲，快手面試有一道畫師畫畫的算法題，很難，就是以這道題為原型。當時我沒做過這道力扣題，面試有點懵，不過之前文章二分查找算法運用寫了兩道類似的比較簡單的題目，外加面試官的提示，把那道題做出來了。

面試做算法題的時候，題目一般都會要求算法的時間復雜度，如果你發(fā)現(xiàn) O(NlogN) 這樣存在對數(shù)的復雜度，一般都要往二分查找的方向上靠，這也算是個小套路。

言歸正傳，如何解決這道數(shù)組分割的問題？

首先，一個拍腦袋的思路就是用回溯算法框架暴力窮舉唄，我簡單說下思路：

你不是要我把nums分割成m個子數(shù)組，然后計算巴拉巴拉又是最大又是最小的那個最值嗎？那我把所有分割方案都窮舉出來，那個最值肯定可以算出來對吧？

怎么窮舉呢？把nums分割成m個子數(shù)組，相當于在len(nums)個元素的序列中切m - 1刀，對于每兩個元素之間的間隙，我們都有兩種「選擇」，切一刀，或者不切。

你看，這不就是標準的回溯暴力窮舉思路嘛，我們根據(jù)窮舉結(jié)果去計算每種方案的最大子數(shù)組和，肯定可以算出答案。

但是回溯的缺點就是復雜度很高，我們剛才說的思路其實就是「組合」嘛，時間復雜度就是組合公式：

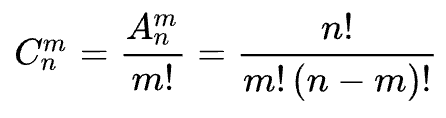
時間復雜度其實是非常高的，所以回溯算法不是一個好的思路，還是得上二分查找技巧，反向思考這道題。

現(xiàn)在題目是固定了m的值，讓我們確定一個最大子數(shù)組和；所謂反向思考就是說，我們可以反過來，限制一個最大子數(shù)組和max，來反推最大子數(shù)組和為max時，至少可以將nums分割成幾個子數(shù)組。

比如說我們可以寫這樣一個split函數(shù)：

//在每個子數(shù)組和不超過max的條件下， //計算nums至少可以分割成幾個子數(shù)組 intsplit(int[]nums,intmax);

比如說nums = [7,2,5,10]，若限制max = 10，則split函數(shù)返回 3，即nums數(shù)組最少能分割成三個子數(shù)組，分別是[7,2],[5],[10]。

如果我們找到一個最小max值，滿足split(nums, max)和m相等，那么這個max值不就是符合題意的「最小的最大子數(shù)組和」嗎？

現(xiàn)在就簡單了，我們只要對max進行窮舉就行，那么最大子數(shù)組和max的取值范圍是什么呢？

顯然，子數(shù)組至少包含一個元素，至多包含整個數(shù)組，所以「最大」子數(shù)組和的取值范圍就是閉區(qū)間[max(nums), sum(nums)]，也就是最大元素值到整個數(shù)組和之間。

那么，我們就可以寫出如下代碼：

/*主函數(shù)，計算最大子數(shù)組和*/ intsplitArray(int[]nums,intm){ intlo=getMax(nums),hi=getSum(nums); for(intmax=lo;max<=?hi;?max++)?{ ????????//?如果最大子數(shù)組和是?max， ????????//?至少可以把?nums?分割成?n?個子數(shù)組 ????????int?n?=?split(nums,?max); ????????//?為什么是?<=?不是?==?？ ????????if?(n?<=?m)?{ ????????????return?max; ????????} ????} ????return?-1; } /*?輔助函數(shù)，若限制最大子數(shù)組和為?max， 計算?nums?至少可以被分割成幾個子數(shù)組?*/ int?split(int[]?nums,?int?max)?{ ????//?至少可以分割的子數(shù)組數(shù)量 ????int?count?=?1; ????//?記錄每個子數(shù)組的元素和 ????int?sum?=?0; ????for?(int?i?=?0;?i?max){ //如果當前子數(shù)組和大于max限制 //則這個子數(shù)組不能再添加元素了 count++; sum=nums[i]; }else{ //當前子數(shù)組和還沒達到max限制 //還可以添加元素 sum+=nums[i]; } } returncount; } //計算數(shù)組中的最大值 intgetMax(int[]nums){ intres=0; for(intn:nums) res=Math.max(n,res); returnres; } //計算數(shù)組元素和 intgetSum(int[]nums){ intres=0; for(intn:nums) res+=n; returnres; }

這段代碼有兩個關鍵問題：

1、對max變量的窮舉是從lo到hi即從小到大的。

這是因為我們求的是「最大子數(shù)組和」的「最小值」，且split函數(shù)的返回值有單調(diào)性，所以從小到大遍歷，第一個滿足條件的值就是「最小值」。

2、函數(shù)返回的條件是n <= m，而不是n == m。按照之前的思路，應該n == m才對吧？

其實，split函數(shù)采用了貪心的策略，計算的是max限制下至少能夠?qū)ums分割成幾個子數(shù)組。

舉個例子，輸入nums = [2,1,1], m = 3，顯然分割方法只有一種，即每個元素都認為是一個子數(shù)組，最大子數(shù)組和為 2。

但是，我們的算法會在區(qū)間[2,4]窮舉max，當max = 2時，split會算出nums至少可以被分割成n = 2個子數(shù)組[2]和[1,1]。

當max = 3時算出n = 2，當max = 4時算出n = 1，顯然都是小于m = 3的。

所以我們不能用n == m而必須用n <= m來找到答案，因為如果你能把nums分割成 2 個子數(shù)組（[2],[1,1]），那么肯定也可以分割成 3 個子數(shù)組（[2],[1],[1]）。

好了，現(xiàn)在 for 循環(huán)的暴力算法已經(jīng)寫完了，但是無法通過力扣的判題系統(tǒng)，會超時。

由于split是單調(diào)函數(shù)，且符合二分查找技巧進行優(yōu)化的標志，所以可以試圖改造成二分查找。

那么應該使用搜索左側(cè)邊界的二分查找，還是搜索右側(cè)邊界的二分查找呢？這個還是要看我們的算法邏輯：

intlo=getMax(nums),hi=getSum(nums); for(intmax=lo;max<=?hi;?max++)?{ ????int?n?=?split(nums,?max); ????if?(n?<=?m)?{ ????????return?max; ????} }

可能存在多個max使得split(nums, max)算出相同的n，因為我們的算法會返回最小的那個max，所以應該使用搜索左側(cè)邊界的二分查找算法。

現(xiàn)在，問題變?yōu)椋涸陂]區(qū)間[lo, hi]中搜索一個最小的max，使得split(nums, max)恰好等于m。

那么，我們就可以直接套用搜索左側(cè)邊界的二分搜索框架改寫代碼：

intsplitArray(int[]nums,intm){ //一般搜索區(qū)間是左開右閉的，所以hi要額外加一 intlo=getMax(nums),hi=getSum(nums)+1; while(lom){ //最大子數(shù)組和上限低了，增加一些 lo=mid+1; } } returnlo; } intsplit(int[]nums,intmax){/*見上文*/} intgetMax(int[]nums){/*見上文*/} intgetSum(int[]nums){/*見上文*/}

這段二分搜索的代碼就是標準的搜索左側(cè)邊界的代碼框架，如果不理解可以參見前文二分查找框架詳解，這里就不展開了。

至此，這道題就通過二分查找技巧高效解決了。假設nums元素個數(shù)為N，元素和為S，則split函數(shù)的復雜度為O(N)，二分查找的復雜度為O(logS)，所以算法的總時間復雜度為O(N*logS)

責任編輯：lq