基礎(chǔ)數(shù)據(jù)結(jié)構(gòu)的融合是成為龐大系統(tǒng)的基石。比如Redis中的跳躍表,數(shù)據(jù)庫索引B+樹等,只有對基礎(chǔ)的數(shù)據(jù)結(jié)構(gòu)足夠的熟悉才能更容易去理解稍微復雜的結(jié)構(gòu),就仿佛我們闖關(guān)打怪一樣,一步一步解鎖直到結(jié)局。今天想和大家一起分享的是常見數(shù)據(jù)結(jié)構(gòu)以及面試中的高頻手撕算法題,一定要去手動寫這些代碼,可說百分之七八十都是這些題,一定要好好掌握。
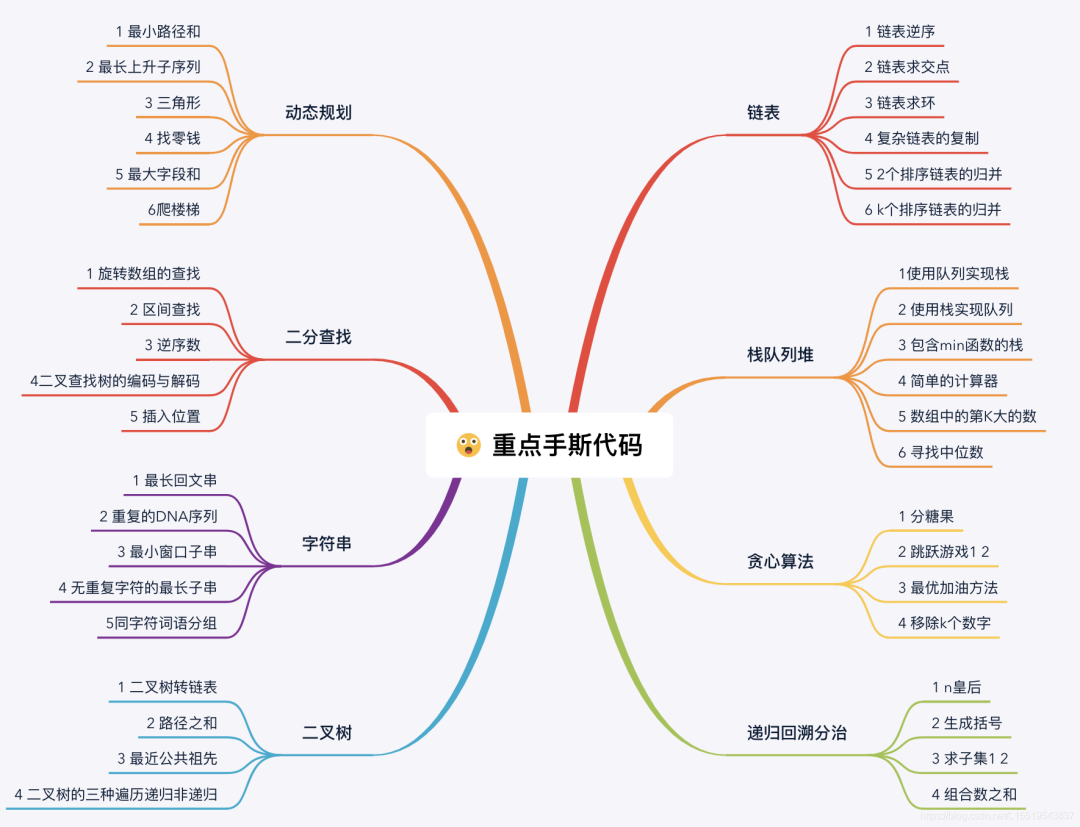
高頻手撕算法合集
1、數(shù)據(jù)結(jié)構(gòu)
鏈表屬于數(shù)據(jù)結(jié)構(gòu)中的線性結(jié)構(gòu)的一種,我們先看看什么是數(shù)據(jù)結(jié)構(gòu)
數(shù)據(jù)結(jié)構(gòu)是:結(jié)構(gòu)的定義+結(jié)構(gòu)的操作
想必大伙兒應該玩兒過拼圖,拼圖之前我們先看看說明書,看看包含幾個部分,然后對這些部分進行拼裝,隨后拼好候進行組合直到完成。
那么數(shù)據(jù)結(jié)構(gòu)中的結(jié)構(gòu)定義是這個數(shù)據(jù)結(jié)構(gòu)長什么樣子,有些什么性質(zhì)?結(jié)構(gòu)的操作意思是這個結(jié)構(gòu)可以支持什么操作,但是不管你怎么的操作,不能破壞了它的結(jié)構(gòu)
2、鏈表定義
一個鏈表是由1個或者多個節(jié)點組成,每個節(jié)點包含兩個信息,一個是數(shù)據(jù)信息,用來存儲數(shù)據(jù),一個是地址信息,用來存儲下個節(jié)點的地址。

鏈表節(jié)點
鏈表結(jié)構(gòu)由一個個節(jié)點組成,我們不需要對結(jié)構(gòu)做任何改變,只需要按照需求修改鏈表結(jié)構(gòu)中的數(shù)據(jù)域即可。從上圖我們知道此事數(shù)據(jù)域類型為整型763,指針域為0x56432,這個地址正好是第二個節(jié)點的地址,所以這兩個節(jié)點在邏輯上是有個指向關(guān)系,也是通過這種方式將兩個節(jié)點進行了關(guān)聯(lián)。
第二個節(jié)點中的指針域為0x0,這是一個特殊的地址,叫做空地址,指向空地址意味著它是這個鏈表結(jié)構(gòu)的最后一個節(jié)點。
那在代碼中是什么樣子呢
structNode{ intdata; structNode*next; };
這個結(jié)構(gòu)很清晰,數(shù)據(jù)域根據(jù)我們的需求而定,想存整型就改成整型,想存字符串就寫字符串。而指針域用來維護整個鏈表結(jié)構(gòu),一般來說直接用即可,如果需要內(nèi)存中的鏈表結(jié)構(gòu),一定要修改節(jié)點內(nèi)部next指針域中存儲的地址值
3、鏈表操作
說到鏈表結(jié)構(gòu),我們習慣性的和數(shù)組聯(lián)系在一起。只是數(shù)組結(jié)構(gòu)在內(nèi)存中是連續(xù)的,而鏈表結(jié)構(gòu)因為指針域的存在,每個節(jié)點在內(nèi)存中存儲的位置未必連續(xù)。下面我們按照數(shù)組的方式給鏈表也編個號。

單鏈表
下面我們定義一個向鏈表插入節(jié)點的函數(shù)
structNode*insert(structNode*head,intind,structNode*a);
第一個參數(shù)為待操作的鏈表的頭結(jié)點地址,也就是第一個節(jié)點的地址
第二個參數(shù)為插入位置
第三個參數(shù)為指針變量,指向要插入的新節(jié)點
簡單的說就是向 head 指向的鏈表的 ind 位置插入一個由 a 指向的節(jié)點,返回值為插入新節(jié)點后的表頭地址。為什么要返回它呢?因為我們插入的節(jié)點很可能在頭部,此時就會改變鏈表的結(jié)構(gòu)且改變頭結(jié)點地址,所以需要返回。
那么我們插入一個元素,顯然會改變鏈表的節(jié)點,操作方法為修改鏈表節(jié)點的 next 指針域即可,那么為了插入成功,我們需要修改哪些節(jié)點呢?
首先是讓 ind - 1 位置的節(jié)點指向 a 節(jié)點,然后是 a 節(jié)點指向原 ind 位置的節(jié)點,也就是說,涉及到兩個節(jié)點的 next 指針域的值的修改,一個是 ind - 1 位置的節(jié)點,一個是 a 節(jié)點自身。我們就可以先找到 ind - 1 位置的節(jié)點,然后再進行相關(guān)操作即可。
structNode*insert(structNode*head,intind,structNode*a){ structNoderet,*p=&ret; ret.next=head; //從虛擬頭節(jié)點開始向后走ind步 while(ind--)p=p->next; //完成節(jié)點的插入操作 a->next=p->next; p->next=a; //返回真正的鏈表頭節(jié)點地址 returnret.next; }
這里非常關(guān)心且非常重要的是虛擬節(jié)點。我們?yōu)槭裁匆胩摂M節(jié)點?是為了讓我們的插入操作統(tǒng)一化?什么是統(tǒng)一化?舉個例子,假設我們現(xiàn)在是在第5個位置插入元素,我們自然需要從頭遍歷到第四個節(jié)點,確定了第四個節(jié)點后,修改相關(guān)的next指針域,也就是如果我們想插入到 nid 位,就需要從頭節(jié)點向后移動 ind-1 步,那么如果插入的位置為0呢?我們總不能走-1步吧,所以這個時候我們只好對ind=0的情況進行單獨的判斷了,這樣明顯是不完美了,所以我們?yōu)榱私y(tǒng)一ind在等于0和不等于0時的情況,引入虛擬節(jié)點。
ok,我們看看是不是方便了。增加了虛擬節(jié)點,如果插入第5個位置,我們只需要向后移動5位,如果插入到0號位置,向后移動0步即可,即p指針指向虛擬節(jié)點不懂,直接將新的節(jié)點插入到虛擬頭結(jié)點后面完事兒。
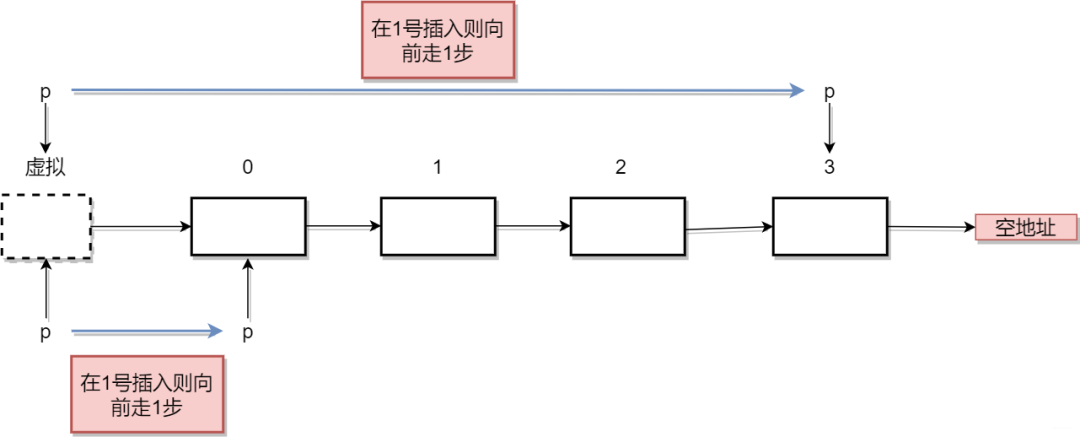
虛擬節(jié)點
好勒,這里出現(xiàn)了第一個重要的技巧。在我們插入鏈表節(jié)點的時候,加上虛擬節(jié)點是個實用技巧。
那么我們看看插入和刪除的操作動態(tài)以及實現(xiàn)方式
3、案例
案例1
我們看個題吧,定義一個快樂數(shù),什么是快樂數(shù),所謂快樂數(shù)即通過有限次變換后等于1 的數(shù)字。怎么變換呢,給出一個非1的數(shù)字,然后出去位數(shù),求各個位數(shù)的平方和,得到數(shù)字A,假設A不死1,那就繼續(xù)對元素A的每一位進行平方和,得到數(shù)字B。。。。知道最后能夠=1
例如,一開始的數(shù)字是 19,經(jīng)過變換規(guī)則 ,得到數(shù)字 82;因為不是 1 ,所以接著做變換,就是 ,再做一次變換 ,最后一次做變換,得到了 1 以后,停止
這個題的難點不是判斷數(shù)是不是快樂數(shù),而是如何判斷一個數(shù)不是快樂數(shù),如果不是快樂數(shù),說明沒有辦法通過有限的次數(shù)到達數(shù)字1,那么到底是 經(jīng)過多少次呢?1k次,10w次?很難確定上限。在說這個問題之前我們先看幾個高頻鏈表練習題
例題1 用數(shù)組判斷鏈表中是否有環(huán)
在上面我們介紹了最后一個節(jié)點指向空,可是你有沒有想過如果鏈表的最后一個節(jié)點不是空地址而是指向鏈表中的一個節(jié)點,這不就是環(huán)了?
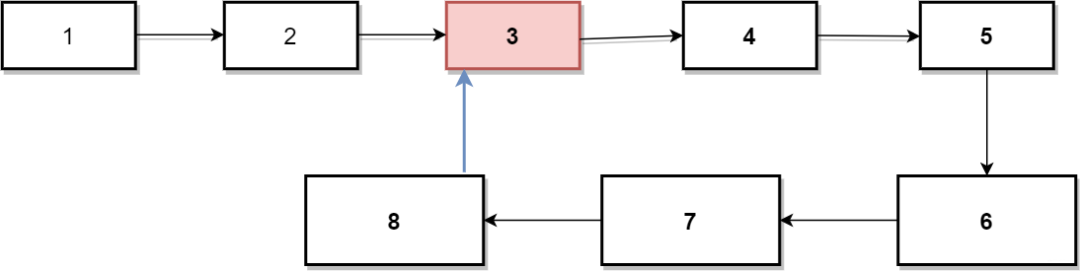
鏈表環(huán)
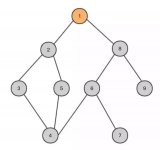
如上圖所示,節(jié)點8指向了3,這樣形成了3,4,5,6,7,8的環(huán)狀結(jié)構(gòu),此時使用指針遍歷鏈表將永無止境。那通過什么辦法判斷是否有環(huán)呢?
使用數(shù)組標記的方法。記錄出現(xiàn)過的節(jié)點信息,每次遍歷新節(jié)點就去數(shù)組查看記錄,這樣的時間復雜度不給力。經(jīng)過第一個節(jié)點,需要在數(shù)組查找0次,第2個節(jié)點,數(shù)組查找1次,第i個節(jié)點,在數(shù)組查找i-1次,直到遍歷第n+1個節(jié)點,查找的總次數(shù)為(n + 1) * n / 2,這樣時間復雜度為O(n^2)。太慢了,給我優(yōu)化
快慢指針法
AB兩位同學跑步,A同學速度快,B同學速度慢,他們并不知道跑道是環(huán)形的,如果是環(huán)形,跑得快的,在足夠的時間終究會從速度慢的B同學經(jīng)過,形成相遇的情況。如果不是環(huán)形,速度快的先到重點,不會相遇---快慢指針法。
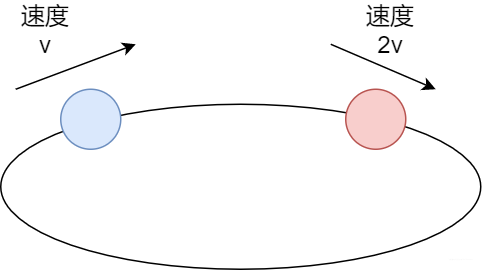
快慢指針
在這里,我們將鏈表當做跑道,跑道上兩個指針,指針A每次走兩步,指針B每次走兩步,如果快的指針先跑到終點注定沒有環(huán),如果兩指針相遇則有環(huán)。
inthasCycle(structNode*head){ if(head==NULL)return0; //p是慢指針,q是快指針 structNode*p=head,*q=head; //每次循環(huán),p走1步,q走2步 do{ p=p->next; q=q->next; if(q==NULL)return0; q=q->next; }while(p!=q&&q); returnp==q; }
3、二分查找初探
說到二分查找,這里就有個笑話了。
小孫同學去圖書館借書,一次性了借了40本書,出圖書館的時候報警了,不知道哪一本書沒有消磁,然后把書放在地上,準備一本本嘗試。
女生的操作被旁邊的阿姨看見了,阿姨說你這樣操作多慢啊,我來教你。于是將樹分為兩摞,拿出第一luo過一下安檢,安檢機器想了,于是阿姨將這摞書分成兩部分,拿出一部分繼續(xù)嘗試,就這樣,阿姨每次減少一半,沒幾次就找到了沒有消磁的書。阿姨嘚瑟的來一句:小姑涼,這就是書中的二分查找算法,你這還得好好學習哇,第二天,圖書館發(fā)現(xiàn)丟了39本書。哈哈哈哈
4、二分查找基礎(chǔ)
最簡單的二分算法即在一個有序數(shù)組中,查找一個數(shù)字X是否存在。注意有序性。那么如何在數(shù)組中查找一個數(shù)
從頭到尾一個一個查找,找到即有數(shù)字x
二分算法即通過確定一個區(qū)間,然后查找區(qū)間的一半和x比較,如果比x大則在x前半段查找。如果比x小則在后半段查找,只需要log2n的比較即可確定結(jié)果。

二分初探
圖中呢,我們以查找 17 這個數(shù)字為例,L 和 R 所圈定的,就是當前的查找區(qū)間,一開始 L= 0,R = 6,mid 所指向的就是數(shù)組的中間位置,根據(jù) L 和 R 計算得到 mid 的值是 3。查看數(shù)組第 3 位的值是 12,比待查找值 17 要小,說明如果 17 在這個有序數(shù)組中,那它一定在 mid 所指向位置的后面,而 mid 本身所指向的數(shù)字已經(jīng)確定不是 17 了,所以下一次我們可以將查找區(qū)間,定位到 mid + 1 到 R,也就是將 L 調(diào)整到 mid + 1 (即數(shù)組第 4
位)的位置。
1 第一種小白寫法
intBinarySerach(vector
面試官發(fā)話了
方法二優(yōu)化版
如果right和left比較的時候,兩者之和可能溢出。那么改進的方法是mid=left+(right-left)/2.還可以繼續(xù)優(yōu)化,我們將除以2這種操作轉(zhuǎn)換為位運算mid=left+((right-left)>>1).
哪有這么簡單的事兒,大多數(shù)的筆試面試中可能會出現(xiàn)下面的幾種情況。
四 、二分的各種變種
這里主要是看看原始數(shù)組有重復數(shù)的情況。
二分
1 查找第一個值等于給定值的情況(查找元素7)
首先7與中間值a[4]比較,發(fā)現(xiàn)小于7,于是在5到9中繼續(xù)查找,中間a[7]=7,但是這個數(shù)7不是第一次出現(xiàn)的。那么我們檢查這個值的前面是不是等于7,如果等于7,說明目前這個值不是第一次出現(xiàn)的7,此時更新rihgt=mid-1。ok我們看看代碼
intBinarySerach(vector
2 查找最后一個值等于給定值的情況
假設nums[mid]這個值已經(jīng)是最后一個元素了,那么它肯定是要找到最后一個值。如果nums[mid]的下一個不等于value,那說明nums[mid]就是我們需要找到最后一個等于給定值的值。
intBinarySerach(vector
3 查找第一個大于等于給定值的情況
如果nums[mid]小于要查找的值,那么我們需要查找在[mid+1,right]之間,所以此時更新為left=mid+1
如果nums[mid]大于給定值value,這個時候需要查看nums[mid]是不是我們需要找的第一個值大于等于給定值元素,如果nums[mid]前面沒有元素或者前面一個元素小于查找的值,那么nums[mid]就是我們需要查找的值。相反
如果nums[mid-1]也是大于等于查找的值,那么說明查找的元素在[left,mid-1]之間,所以我們需要將right更新為mid-1
intBinarySerach(vector
4 查找第一個大于等于給定值的情況
如果nums[mid]小于要查找的值,那么我們需要查找在[mid+1,right]之間,所以此時更新為left=mid+1
如果nums[mid]大于給定值value,這個時候需要查看nums[mid]是不是我們需要找的第一個值大于等于給定值元素,如果nums[mid]前面沒有元素或者前面一個元素小于查找的值,那么nums[mid]就是我們需要查找的值。相反
如果nums[mid-1]也是大于等于查找的值,那么說明查找的元素在[left,mid-1]之間,所以我們需要將right更新為mid-1
intBinarySerach(vector
5 查找最后一個小于等于給定值的情況
如果nums[mid]小于查找的值,那么需要查找的值肯定在[mid+1,right]之間,所以我們需要更新left=mid+1
如果nums[mid]大于等于給定的value,檢查nums[mid]是不是我們的第一個值大于等于給定值的元素
intBinarySerach(vector
4、隊列
例子:滑動窗口最大值
隊列回憶:
火車站買票應該都經(jīng)歷過,窗口小姐姐每次服務排在最前面的那個人,買完票則從頭部離開,后面人往前一步接替離開的人繼續(xù)購票,這就是典型的隊列結(jié)構(gòu)。
計算機中的隊列和其類似,先到先得,先入先出,每個元素從尾部入隊,從頭部處理完出隊
隊列定義
單調(diào)隊列
假設將學生從高年級到低年級排列,隨著時間的推移,高年級同學從隊列頭部畢業(yè),低年級從尾部進入。大部分學校都有校隊,假設小林高三,我高二,小七高一,小林畢業(yè)接班的是我,我畢業(yè),很可能就是小七接班,而當我進隊的那一刻,小七即使進的早但是戰(zhàn)斗力沒我高,所以小七是永遠沒計劃被選中啦。所以,縱觀全隊,不僅有著隊列的性質(zhì),也有著單調(diào)的性質(zhì),所以就是單調(diào)隊列。
為什么需要單調(diào)隊列
比較明顯的作用是,用來維護隊列處理順序中的區(qū)間最大值。
高頻面試題----滑動窗口最大值
滑動窗口沒向后滑動一位,就有一個元素從隊首出隊,同時也會有個元素從隊尾入隊。這個題需要求區(qū)間的最大值:意味著需要維護在隊列處理順序中的區(qū)間最大值,直接上代碼附上注釋
#defineMAX_N1000 intq[MAX_N+5],head,tail; voidinterval_max_number(int*a,intn,intm){ head=tail=0; for(inti=0;i=m){ printf("interval(%d,%d)",i-m+1,i); printf("=%d ",a[q[head]]); } } return; }
5、棧與單調(diào)棧
棧結(jié)構(gòu)對應于隊列,可以將棧想象為一個只有單出口的羽毛球筒,羽毛球只能從單一的入口放入和取出。假設我們將1,2,3三個球放進球桶,如果取出來此時就是3,2,1。性質(zhì)就很明顯了,先進后出的結(jié)構(gòu)
棧結(jié)構(gòu)本身維護的是一種完全包含的關(guān)系。這種包含關(guān)系在函數(shù)之間的運行體現(xiàn)的玲離盡致,也就是一種包含關(guān)系,如果主函數(shù)調(diào)用函數(shù)B,那么函數(shù)B一定會在主函數(shù)結(jié)束之前結(jié)束。
單調(diào)棧
此時應該了解了棧和隊列,那么我問你,你覺得棧和隊列最大的區(qū)別是啥?
你可能毫不猶豫的可以回答棧是先進后出,隊列是先進先出。ok,那我再問你,堵住了出口的單調(diào)隊列和棧有什么區(qū)別?這是不是就沒什么區(qū)別了,單調(diào)隊列為了維護其單調(diào)性,在入隊的時候會將違反單調(diào)性的元素彈出去,這就相當于棧的同一段進出,是的,堵住出口的單調(diào)隊列就是我們現(xiàn)在要說的單調(diào)棧,目前以單調(diào)遞減棧為例
單調(diào)棧
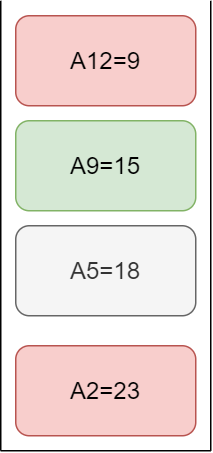
當序列中的12號元素入棧以后,此時單調(diào)棧有4個元素,從棧底到棧頂分別為23,18,15,9,按照原始序列為2 5 9 12。此時我們關(guān)注12號元素和9號元素的關(guān)系。如果12號元素入棧,為了保證棧的單調(diào)遞減性,最終放在9號上面,此時我們雖然不是第十個元素和十一號元素值多少,但是這兩個元素的值一定是比9號元素小,這就是單調(diào)棧的性質(zhì)。所以,單調(diào)隊列是用來維護區(qū)最值的高效結(jié)構(gòu),單調(diào)棧呢是維護最近大于或小于的高效結(jié)構(gòu)。下面看個例子
題目:判斷括號序列是否合法
示例 合法
({})
示例 非合法
([)]
publicbooleanisValid(Strings){ Stack
6、遞推套路
在分享遞推之前,先和大家分享與之緊密的數(shù)學原理:容斥原理
在計數(shù)問題中,為了保證計數(shù)的準確程度,通常會保證兩個問題,第一個問題是沒有重復,第二個問題是沒有遺漏。這兩個問題相對來說,第二點比較容易做到。比如對某地區(qū)進行爆炸式轟炸,為了保證炸的覆蓋面,足夠多的炸彈即可,但是如果保障一塊土地只能炸一次就比較難搞了。那么容斥原理就是解決這個問題
容斥原理是什么?
先不考慮重疊的情況,先將所有對象數(shù)目計算出來,然后將重復計算的排斥出去,是的,計算的結(jié)果不僅不遺漏也不重復。簡單的說就是在計算的過程中,如果加多了就減去多的部分,如果減多了就加回來一部分,直到不多不少。
我們看一個兔子繁殖問題
假設有一片草原上,莫名其妙來了一只外星兔子,這種外星兔子呢,第一個月的時候是幼體,第二個月成長為成體,從第三個月開始,成體兔子每個月都會產(chǎn)生出一只克隆體的幼體兔子,而且這種兔子不會衰老,一旦成體以后,就會一直生下去。按照這種情況,請你計算出第 n 個月,草原上有多
此時給出前面6個月的情況
六個月兔子情況
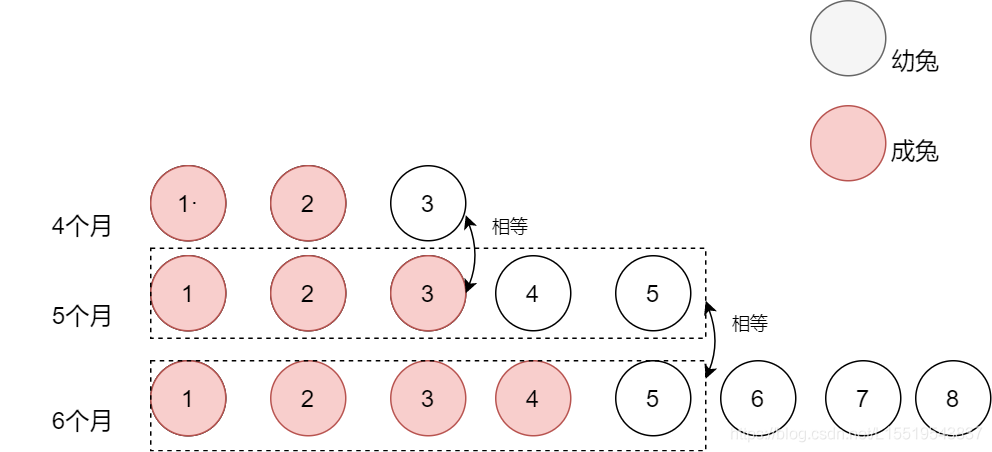
從上圖我們可以發(fā)現(xiàn),從第一個月到第六個月,草原上的兔子數(shù)量分別為1,1,2,3,5,8
第六個月共有8只兔子,其中包含5只成兔,3只幼兔,為什么是5只成兔,因為第六個月的兔子數(shù)量等于第五個月的兔子總數(shù),六個月的3只幼兔是等于第四個月的兔子數(shù)量
后三個月情況
結(jié)論就比較清晰了:從第三個月開始,第n個月的兔子數(shù)量等于該月的成兔數(shù)量與幼兔數(shù)量之和,也就是等于第n-1個月的兔子數(shù)量與第n-2兔子數(shù)量之和。這種根據(jù)前面的數(shù)量來推后面的數(shù)量的情況叫做遞推,那么遞推算法套路通常是怎么樣呢
確定遞推的狀態(tài),多畫圖前面幾步
推導遞推公式
程序的編寫
我們根據(jù)三步走的方式來闡釋解決兔子的這個問題
f(n)表示n個月兔子的數(shù)量
遞推公式(第一個月合第二個月兔子的數(shù)量為1,到了第三個月即等于前面兩個月之和)
遞推公式
案例2 湊錢幣問題
用 1 元、2 元、5 元、10 元、20 元、50 元和 100
確定遞推狀態(tài),需要分析自變量與因變量,自變量兩個分別為幣種種類和拼湊的錢幣數(shù)量,因變量1個為方案總數(shù),因此我們的狀態(tài)定義為f(i,j),i種錢幣,拼湊j元錢的方案總數(shù)。比如f [3][10]即使用三種錢幣,湊出10元的方案總數(shù)
假設我們不使用第三種錢幣,那么此時等價于使用前兩種錢幣拼湊10元錢的方案總數(shù),即f[2][10]。如果使用至少1張5塊錢,那么我們在這些方案中去掉一張5元錢,剩下的方案數(shù)為f[3][5],所以此時的遞推公式為f[3][10] = f[2][10] + f[3][5]。這只是一般情況,假設我們沒有使用第i種錢幣,拼湊j元的方案為f(i-1,j),代表使用前i-1種錢幣的方案總數(shù)。剩下的使用了第i中錢幣,由于都存在第i錢幣1張,假設第i種錢幣的面額為val[i],那么此時我們的前i種錢幣,湊j-val[i]的錢數(shù),此時方案總數(shù)為f(i,j-val[i]);所以公式為f(i,j)=f(i-1,j)+f(i,j-val[i])
推理
7、動態(tài)規(guī)劃
動態(tài)規(guī)劃通常簡稱DP(dynamic programming),如果按照問題類型來劃分,將分為線性DP、區(qū)間DP,數(shù)位DP等等,每當說到動態(tài)規(guī)劃就會想最優(yōu)子結(jié)構(gòu),重疊子問題等等,這些詞匯苦澀難懂,不要慌,再難的問題也是建立在基礎(chǔ)問題上,逐步拆分,這也是動態(tài)規(guī)劃的思想,相信通過下面動態(tài)規(guī)劃四步走的方式,加上習題的練習,一定會讓你對動態(tài)規(guī)劃有個新的理解。
四個步驟分為:狀態(tài)定義,狀態(tài)轉(zhuǎn)移方程,正確性的證明和實現(xiàn)
狀態(tài)定義
其實上面說遞推的時候就已經(jīng)有所涉及狀態(tài)定義,通常在推導的過程中,如果感覺推不下去了,很有可能就是我們的狀態(tài)定義出現(xiàn)了問題。
第一個狀態(tài):dp[i][j]代表從起始點到(I,j)路徑的最大值
第二個狀態(tài):dp[i][j]代表從底邊的某個點出發(fā),到達(i,j)路徑的最大值
狀態(tài)轉(zhuǎn)移方程
上面的兩種狀態(tài)定義對應這里兩個轉(zhuǎn)移方向。
狀態(tài)轉(zhuǎn)移過程
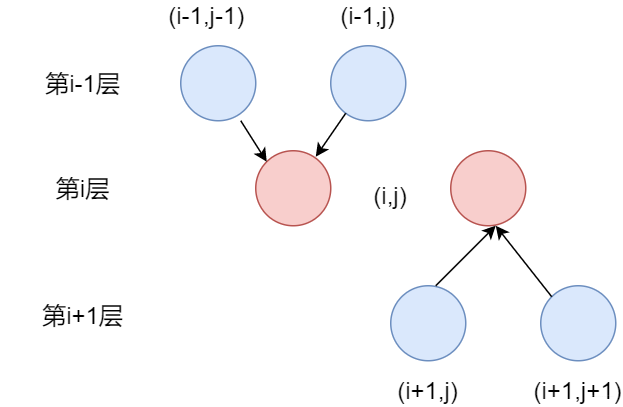
如上圖所示,我們想要求得dp[i][j],需要知道dp|[i-1]|[j-1]和dp[i-1][j]的值。因為只有(i - 1, j - 1) 和 (i - 1, j) 這兩個點,才能能走到 (i, j)此時的狀態(tài)轉(zhuǎn)移方程為
第一種狀態(tài)轉(zhuǎn)移方程dp[i][j] = max(dp[i - 1][j - 1], dp[i - 1][j]) + val[i][j]
第二冊中狀態(tài)轉(zhuǎn)移方程dp[i][j] = max(dp[i + 1][j], dp[i + 1][j + 1]) + val[i][j]
從這里可以知道我們的狀態(tài)定義不一樣,我們的轉(zhuǎn)移方程就很不一樣吧
正確性證明
數(shù)學歸納法通常采用三步走的方式,常用的正確性證明方法為數(shù)學歸納法。
第一步,第一個階段所有dp值可以輕松獲得,也就是初始化dp[1][1],等于val[1][1]
第二步,假設如果第i-1階段的所有狀態(tài)值都正確得到,那么根據(jù)狀態(tài)方程dp[i][j]=max(dp[i - 1][j], dp[i - 1][j + 1]) + val[i][j] 來說,此時就可以計算得到第i階段中的素有狀態(tài)值
第三步:得出結(jié)論,所有的狀態(tài)值計算正確
我們繼續(xù)分析動態(tài)規(guī)劃問題中的0/1背包問題,通常分為三類,0/1背包問題,完全背包問題和多重背包問題。
0/1背包問題是另外兩種背包問題的基礎(chǔ),簡單描述一下,假設有個背包,載重上限為W,此時有n個物品,第i個物品的重量是wi,價值為vi,那么在不超過背包重量上限的前提下,能獲得的最大物品價值總和?同樣我們采用四步走的方式
狀態(tài)定義
首先分析背包問題中的自變量和因變量,其中因變量比較好確定,就是所求最大價值總和,自變量呢,在此自變量為物品種類和背包承重上限,因為這兩者會影響價值總和的最大值,所以我們設置一個二維狀態(tài)。dp[i][j]代表使用前i個物品,背包最大載重為j的情況下最大價值總和。
狀態(tài)方程
說白了就是找映射函數(shù),dp[i][j]的表達式。我們將dp[i][j]分為兩大類,第一類是不選擇第i個物品最大價值和,第二類為選擇了第i個物品的最大價值和。然后在兩者中選擇最大值就是價值更大的方案。
如果選擇第i個物品,此時的最大價值為dp[i-1][j-wi]+vi,既然選擇了第i個商品,那么就需要留出一個位置,那么此時對于剩余的i-1個商品的載重空間就只剩下j-wi了,此時i-1個物品選擇的最大價值和為dp[i-1][j-wi],然后加上vi就是當前獲得最大價值和。所以轉(zhuǎn)移方程為
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i])
正確性證明
首先dp[0][j]=0,意味著沒有物品的時候,無論背包限重多少,能夠得到的最大價值和都是0,所以k0爭取
其次,假設我們已經(jīng)獲取i-1個物品的價值最大值,所有dp[i-1]的值,那么根據(jù)狀態(tài)方程,我們能知道所有dp[i]的值
最后兩步聯(lián)合,整個求解對于任意dp[i][j]成立
實現(xiàn)
#defineMAX_V10000 #defineMAX_N100 intv[MAX_N+5],w[MAX_N+5]; intdp[MAX_N+5][MAX_V+5]; intget_dp(intn,intW){ //初始化dp[0]階段 for(inti=0;i<=?W;?i++)?dp[0][i]?=?0; ????//?假設?dp[i?-?1]?成立,計算得到?dp[i] ????//?狀態(tài)轉(zhuǎn)移過程,i?代表物品,j?代表背包限重 ????for?(int?i?=?1;?i?<=?n;?i++)?{ ???????????for?(int?j?=?0;?j?<=?W;?j++)?{ ????????//?不選擇第?i?種物品時的最大值 ????????dp[i][j]?=?dp[i?-?1][j]; ????????//?與選擇第?i?種物品的最大值作比較,并更新 ????????if?(j?>=w[i]&&dp[i][j]
8、貪心
其實我們大學學習的好幾種應用都是采用了貪心的算法啊,比如Huffman Coding,Prim最小生成樹等
先來看一道之前美團的一道筆試題--跳一跳
有n個盒子排成一行,每個盒子上面有一個數(shù)字a[i],表示最多能向右跳a[i]個盒子;小林站在左邊第一個盒子,請問能否到達最右邊的盒子?比如說:[1, 2, 3, 0, 4] 可以到達第5個盒子;[3, 2, 1, 0, 4] 無法到達第5個盒子;
思路:自然而然的想法,盡可能的往右邊跳,看最后能夠到達,從第一個盒子開始從右遍歷,對于每個經(jīng)過的盒子,不斷地更新maxRight值。那么貪心算法的思考過程通常是怎么樣的?
類似于動態(tài)規(guī)劃,大事化小,小事化了。所謂大事化小,將大的問題,找到和子問題的重復部分,將復雜問題拆分為小的問題。小事化了,通過對小事的打磨找到較為核心的策略。上例子
分糖果問題
我們有 m 個糖果和 n 個孩子。我們現(xiàn)在要把糖果分給這些孩子吃,但是糖果少,孩子多(m
對于一個孩子來說,如果小的糖果可以滿足,那么就沒必要用更大的糖果
對糖果的大小需求的孩子更容易被滿足,所以我們可以從需求小得孩子開始分配糖果
因為滿足一個需求大的孩子跟滿足一個需求小的孩子,對我們期望值的貢獻是一樣的
我們每次從剩下的孩子中,找出對糖果大小需求最小的,然后發(fā)給他剩下的糖果中能滿足他的最小的糖果,這樣得到的分配方案,也就是滿足的孩子個數(shù)最多的方案
#include
責任編輯:lq
思路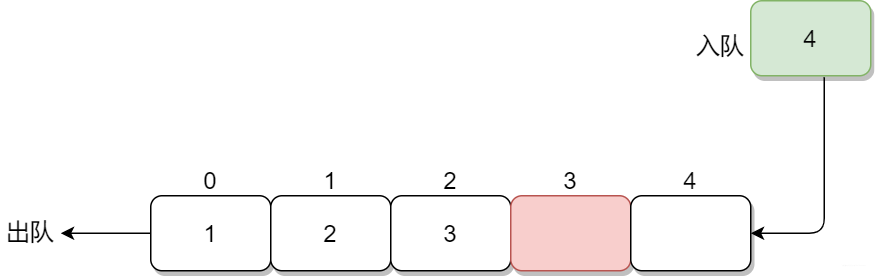
{()}
(((){}
少只兔子?

元湊成 1000 元錢,總共有多少種方案
-
算法
+關(guān)注
關(guān)注
23文章
4601瀏覽量
92677 -
數(shù)據(jù)結(jié)構(gòu)
+關(guān)注
關(guān)注
3文章
573瀏覽量
40095 -
鏈表
+關(guān)注
關(guān)注
0文章
80瀏覽量
10547
原文標題:高頻手撕算法合集來了!
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數(shù)據(jù)結(jié)構(gòu)】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
DDC264配置寄存器數(shù)據(jù)寫入和320 DCLK時鐘脈沖后的回讀數(shù)據(jù)結(jié)構(gòu)是什么?
視覺軟件HALCON的數(shù)據(jù)結(jié)構(gòu)
常見手插元件識別

嵌入式常用數(shù)據(jù)結(jié)構(gòu)有哪些
電路中怎樣消除高頻干擾
面試嵌入式工作,會被問什么問題?

揭秘編程核心:基本數(shù)據(jù)結(jié)構(gòu)與算法思想詳解




 常見數(shù)據(jù)結(jié)構(gòu)以及面試中的高頻手撕算法題
常見數(shù)據(jù)結(jié)構(gòu)以及面試中的高頻手撕算法題











評論