系統和設計工程師通常使用噪聲系數來確保最佳信號性能。但是,在信號鏈中使用混頻器給直接的噪聲圖分析帶來了挑戰。本教程首先檢查噪聲系數的基本定義,然后繼續對包括混頻器的級聯模塊進行基于方程的分析,然后再采用典型的實驗室技術來測量噪聲系數。在探索將Y因子方法用于混頻器噪聲圖測量之前,本教程還涵蓋了噪聲溫度和Y因子噪聲測量的概念。討論了雙邊帶(DSB)和單邊帶(SSB)噪聲圖測量的示例。
簡介
本教程解決了現代無線電接收機中的噪聲系數問題。它討論了導致接收機系統中NF的最常見因素,以及有助于實現所需測量結果的數學方法。探索了無線電接收機的不同部分,并重點介紹了每個部分的NF分析。
噪聲系數的一般概念已得到系統和電路設計人員的充分理解并廣泛使用。特別是,它用于傳達產品定義者和電路設計人員對噪聲性能的要求,并預測接收器系統的整體靈敏度。
當混頻器是信號鏈的一部分時,就會出現噪聲圖分析的主要困難。所有實際混頻器將RF頻譜折疊在本地振蕩器(LO)頻率附近,從而產生一個輸出,其中包含根據fOUT = | fRF – fLO |兩側頻譜的總和。在外差架構中,這些貢獻之一通常被認為是虛假的,而另一貢獻是預期的。因此,很可能采用圖像拒絕濾波或圖像消除方案來大大消除這些響應之一。在直接轉換接收器中,情況有所不同。兩個邊帶(高于和低于fRF = fLO)都被轉換并用于有用信號。因此,這確實是混頻器的雙邊帶(DSB)應用。
工業中通常使用的各種定義在不同程度上解釋了噪聲折疊。例如,傳統的單邊帶噪聲因子FSSB假設允許來自兩個邊帶的噪聲折疊成輸出信號。但是,只有一個邊帶可用于傳送所需信號。假定兩個響應的轉換增益相等,自然會導致噪聲系數增加3dB。相反,DSB噪聲系數假定混頻器的兩個響應都包含有用信號的一部分,因此,噪聲折疊(以及相應的信號折疊)不會影響噪聲系數。DSB噪聲系數可用于直接轉換接收器以及射電天文接收器中。然而,更深入的分析表明,對于設計人員來說,僅針對給定的應用選擇合適的噪聲系數“風味”,然后在標準Friis方程中替換相應的數字是不夠的。這樣做會導致分析上的錯誤,如果在確定系統噪聲系數時,混頻器或混頻器之后的組件起著不可忽略的作用,則分析可能會變得尤為嚴重。
混合器噪聲的概念模型
可視化混合器噪聲貢獻的一種方法是考慮混合器的概念模型(圖1)。該模型基于安捷倫Genesys仿真程序提供的模型。
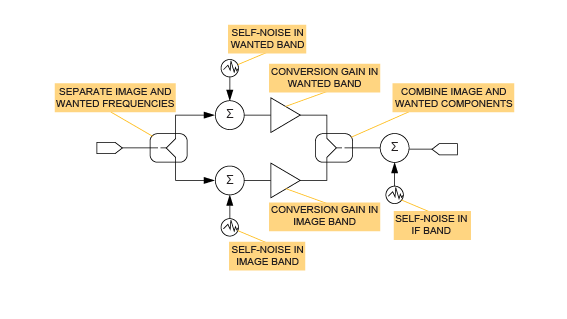
混頻器噪聲貢獻。
在此模型中,輸入信號分為兩個獨立的信號路徑,一個代表LO上方的RF頻率,另一個代表LO下方的頻率。每條路徑在混頻器中都要經過獨立的加性噪聲??處理,并且要應用獨立量的轉換增益。最后,兩條路徑被轉換為IF頻率,并與混頻器輸出級中可能產生的其他噪聲貢獻相加。在所需頻帶和圖像頻帶中,每單位帶寬的自噪聲功率可能會不同;相應的轉換增益也可能不同。
為方便起見,我們可以將所有噪聲源引用到輸出,并以全局噪聲項NA進行收集,NA表示從混頻器輸出端口獲得的每單位帶寬的總附加噪聲功率。
NA = NSGS + NIGI + NIF
請注意,NA完全不取決于混頻器輸入端口上信號的存在與否。
總結了混頻器的內部噪聲源之后,我們現在來看歸因于源端接的噪聲(圖2)。我們確定了兩個離散的噪聲源,分別代表由于輸入端在所需頻率和鏡像頻率處的輸入而引起的輸入噪聲密度。我們必須將它們視為獨立的數量,因為應用電路會導致其中一個衰減,而另一個會以低損耗傳輸到混頻器的RF輸入端口。如果圖像和所需的RF頻率很好地分開并且采用了頻率選擇匹配,則可能是這種情況。
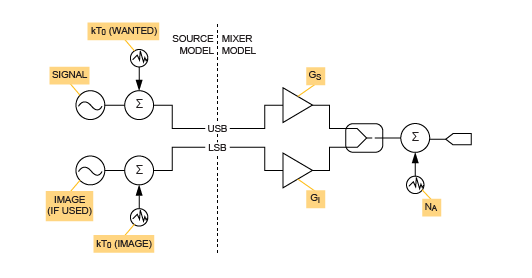
源噪聲和混頻器噪聲貢獻。
在寬帶匹配的情況下,我們可以寫為NOUT = NA + kT0GS + kT0GI。但是,如果在所需的RF頻率下對混頻器進行高Q頻率選擇匹配,則由于源端接在鏡像頻率處而在輸出端產生的噪聲可能可以忽略不計,從而導致NOUT = NA + kT0GS。通常,我們可以將系數α分配給在鏡像頻率下可用于混頻器輸入端口的輸入源端接噪聲功率的有效分數。因此,NOUT = NA + kT0GS +αkT0GI,其中α是0≤α≤1范圍內的特定應用系數。稍后我們將看到應用中的有效噪聲系數取決于α的值。
異源接收器
我們可以通過圖3中的示例看到如何在較大的級聯分析中應用有效噪聲系數。要計算整個鏈的級聯噪聲系數,我們需要封裝混頻器及其相關的LO和圖像抑制濾波,如下所示:具有特定增益和噪聲系數的等效兩端口網絡。該兩端口網絡的有效噪聲因子為FSSBe = 2(FDSB – 1)+ 1,因為前面的濾波器很好地抑制了圖像頻率處的終端噪聲。
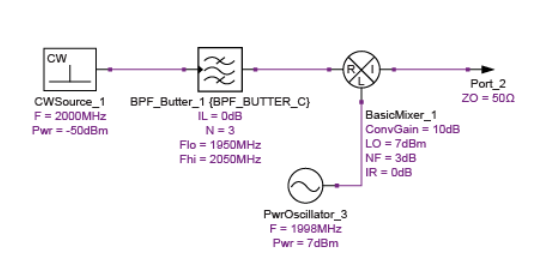
在相鄰系統塊的上下文中,外差混頻器。
請注意,適用的噪聲系數既不是混頻器的DSB噪聲也不是SSB噪聲系數。相反,它是一個有效的噪聲系數,介于這兩個值之間。在這種情況下,DSB噪聲系數為3dB,如上所述,兩端口網絡的等效噪聲系數可以計算為4.757dB。如下表所示,在整體級聯計算中使用該值會導致系統噪聲系數為7.281dB。手動計算表明,此結果與標準Friis方程式一致,混頻器噪聲系數為4.757dB。

系統中外差混頻器的級聯性能模擬
通常,當用等效的兩端口網絡代替混頻器及其相鄰組件時,輸入端口應該是信號流中拒絕圖像響應的最新節點。輸出端口應該是圖像和所需響應組合在一起的最早節點(通常是混頻器的輸出端口)。如果該架構無法有效地抑制混頻器的圖像響應,則未經修改就無法使用Friis方程。
結論
在本教程中,我們看到,在混頻器屬于接收器級聯的一部分的情況下,使用混頻器噪聲系數的DSB或SSB版本,級聯噪聲因子的Friis公式通常無效。如果使用濾波器在很大程度上消除了接收器的圖像響應,則可以用等效的兩端口網絡代替混頻器,濾波器和LO子系統。但是,必須考慮到耦合到混頻器輸入端口的源端接的頻率選擇性,由DSB噪聲系數計算得出的噪聲系數。
我們還發現,相同的物理結構可能具有不同的有效噪聲系數,具體取決于信號是分布在LO周圍還是完全分布在LO的一側(即,應用分別是DSB或SSB)。通過在LIF模式下使用復雜的接收器而導致的SNR的3dB損失可以(通常)通過適當使用鏡像抑制合并,復雜濾波或等效基帶處理來恢復。
Y因子測量將評估混頻器的DSB噪聲系數,除非采取特殊措施濾除鏡像頻率處的寬帶噪聲刺激。這是與先前導出的級聯方程一起使用的適當值。當使用濾波器嘗試獲得SSB噪聲系數時,有必要考慮所用濾波器的插入損耗。此外,通過濾波器抑制源端接圖像噪聲的程度可能會導致偏離SSB噪聲系數的經典定義。匹配衰減器的使用可以在很大程度上克服此問題,前提是所使用的衰減量與噪聲源的ENR相比不會過多。
編輯:hfy
-
濾波器
+關注
關注
160文章
7749瀏覽量
177737 -
接收器
+關注
關注
14文章
2458瀏覽量
71808 -
混頻器
+關注
關注
10文章
679瀏覽量
45621
發布評論請先 登錄
相關推薦
無線時鐘接收器怎么連接
無線充電接收器原理是什么
無線充電接收器怎么使用
單邊帶調制和雙邊帶調制的區別
模擬無源濾波器設計:兩種不同的90°移相網絡
ATA-4051高壓功率放大器在仿生水下聲接收器設計中的應用
單邊低噪聲放大器設計方案
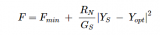
AM、FM、SSB全模式30kHz SDR接收器設計
SRRC新規開始實施,諾思新品可提升WiFi 2.4G邊帶抑制




 接收器的雙邊帶(DSB)和單邊帶(SSB)噪聲圖測量示例
接收器的雙邊帶(DSB)和單邊帶(SSB)噪聲圖測量示例











評論