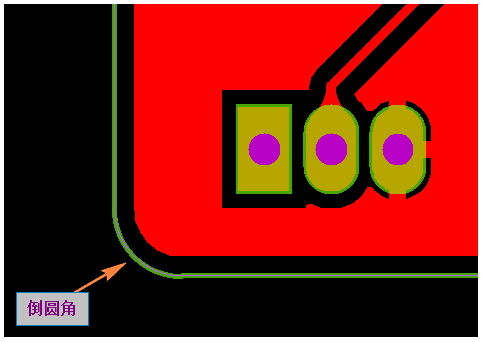
當 PCB 外形是直角時， 通常工程制作外形 （鑼帶） 時， 會將直角或尖角的地方倒成圓角， 主要是為了防止板邊容易劃傷板且容易扎傷人

所以當客戶沒有特殊要求時， PCB 外形是直角一般會默認倒角 0.5mm 圓角（如下圖所示）

一。 PCB 板邊倒圓角點分析

原 PCB 外形 如下圖圖示： 看了這個 PCB 外形， 產(chǎn)生有 2 個問題點。

1. 外形中哪些點需倒圓角？

2. 如何怎么倒圓角？

1. 外形中哪些點需倒圓角？

看下圖： PCB 外形倒圓角的點， 剛好就是我們凸包需求出的點， 接下來我們將玩轉(zhuǎn)凸包了， 只要求出凸包， 那么就可以實現(xiàn) PCB 板邊倒圓角啦。

求凸包的算法： 我們可以借鑒算法導論中的查找凸包的算法（加以改進得到新的求凸包方法， 詳見［方法一］ 與［方法二］ ）

2. 如何怎么倒圓角？

在下面有說明倒角方法。

二。 求凸點

方法一求凸點：［采用多輪遍歷， 一遍一遍將凹點踢除， 剩于的即是凸點］

方法一求凸點： 代碼

/// 《summary》

/// 求最大多邊形最大凸包 1 ［采用多輪遍歷將凹點踢除， 剩于的即是凸點］

/// 《/summary》

/// 《param name=“gSur_Point_list”》《/param》

/// 《returns》《/returns》

public List《gSur_Point》 s_convex_polyon1（List《gSur_Point》 gSur_Point_list）

{

add addCOM = new add（）;

bool isOK = true;

List《gSur_Point》 PointList = new List《gSur_Point》（）;

var isCCW = s_isCCW（gSur_Point_list）;

int sum = gSur_Point_list.Count（） - 1;

int n = gSur_Point_list.Count（）;

for （int i = 0; i 《n; i++）

{

int IndexPre = （i - 1） % sum;

if （IndexPre == -1） IndexPre = sum - 1;

int IndexCurrent = i % sum;

int IndexNext = （i + 1） % sum;

if （gSur_Point_list［IndexPre］.type_point》 0） continue;

if （gSur_Point_list［IndexCurrent］.type_point》 0） continue;

var multiVal = multi（gSur_Point_list［IndexPre］.p， gSur_Point_list［IndexCurrent］.p， gSur_Point_list［IndexNext］.p）;

if （（isCCW && multiVal》 0） || （！isCCW && multiVal 《0））

PointList.Add（gSur_Point_list［IndexCurrent］）;

else

isOK = false;

}

List《gSur_Point》 Point2List = new List《gSur_Point》（PointList）;

while （！isOK）

{

isOK = true;

PointList.Clear（）;

PointList.AddRange（Point2List）;

Point2List.Clear（）;

sum = PointList.Count（） - 1;

n = PointList.Count（）;

for （int i = 0; i 《n; i++）

{

int IndexPre = （i - 1） % sum;

if （IndexPre == -1） IndexPre = sum - 1;

int IndexCurrent = i % sum;

int IndexNext = （i + 1） % sum;

var multiVal = multi（PointList［IndexPre］.p， PointList［IndexCurrent］.p， PointList［IndexNext］.p）;

if （（isCCW && multiVal》 0） || （！isCCW && multiVal 《0））

Point2List.Add（PointList［IndexCurrent］）;

else

isOK = false;

}

}

return Point2List;

}

方法二求凸包：［采用一邊遍歷找出凸點并加入隊列， 并同時將隊列中的凸點隊列中找出凹點踢除］

方法二求凸包代碼：

/// 《summary》

/// 求最大多邊形最大凸包 2 ［采用一邊遍歷找出凸點并加入隊列， 并同時將隊列中的凸點隊列中找出凹點踢除］

/// 《/summary》

/// 《param name=“gSur_Point_list”》《/param》

/// 《returns》《/returns》

public List《gSur_Point》 s_convex_polyon2（List《gSur_Point》 gSur_Point_list）

{

Stack《gSur_Point》 StackPoint = new Stack《gSur_Point》（）;

var isCCW = s_isCCW（gSur_Point_list）;

int sum = gSur_Point_list.Count（） - 1;

int n = gSur_Point_list.Count（）;

for （int i = 0; i 《n; i++）

{

int IndexPre = （i - 1） % sum;

if （IndexPre == -1） IndexPre = sum - 1;

int IndexCurrent = i % sum;

int IndexNext = （i + 1） % sum;

if （gSur_Point_list［IndexPre］.type_point》 0） continue;

if （gSur_Point_list［IndexCurrent］.type_point》 0） continue;

var multiVal = multi（gSur_Point_list［IndexPre］.p， gSur_Point_list［IndexCurrent］.p， gSur_Point_list［IndexNext］.p）;

if （（isCCW && multiVal》 0） || （！isCCW && multiVal 《0））

{

L1：

if （StackPoint.Count》 1）

{

var Top1Point = StackPoint.Pop（）;

var Top2Point = StackPoint.Peek（）;

multiVal = multi（Top2Point.p， Top1Point.p， gSur_Point_list［IndexCurrent］.p）;

if （（isCCW && multiVal》 0） || （！isCCW && multiVal 《0））

StackPoint.Push（Top1Point）;

else

goto L1;

}

StackPoint.Push（gSur_Point_list［IndexCurrent］）;

}

}

return StackPoint.Reverse（）.ToList（）;

}

方法三求凸包：［按算法導論 Graham 掃描法 各節(jié)點按方位角 + 距離 逆時針排序 依次檢查， 當不屬凸點于則彈出］

方法三求凸包代碼

/// 《summary》

/// 求最大多邊形最大凸包 5 ［按算法導論 Graham 掃描法 各節(jié)點按方位角 + 距離 逆時針排序 依次檢查， 當不屬凸點于則彈出］

/// 由于把各點的排列順序重新排序了， 只支持折線節(jié)點（當存在弧節(jié)點時會出異常 ！！！）

/// 《/summary》

/// 《param name=“gSur_Point_list”》《/param》

/// 《returns》《/returns》

public List《gSur_Point》 s_convex_polyon3（List《gSur_Point》 gSur_Point_list）

{

var LeftBottomPoint = gSur_Point_list.OrderBy（tt =》 tt.p.y）.ThenBy（tt =》 tt.p.x）.FirstOrDefault（）;

gSur_Point_list.RemoveAt（gSur_Point_list.Count - 1）;

gSur_Point_list.ForEach（tt =》

{

tt.Value = p2p_di（LeftBottomPoint.p， tt.p）;

tt.Angle = p_ang（LeftBottomPoint.p， tt.p）;

}

）;

gSur_Point_list = gSur_Point_list.OrderBy（tt =》 tt.Angle）.ThenBy（tt =》 tt.Value）.ToList（）;

gSur_Point_list.Add（gSur_Point_list［0］）;

Stack《gSur_Point》 StackPoint = new Stack《gSur_Point》（）;

var isCCW = true;

int sum = gSur_Point_list.Count（） - 1;

int n = gSur_Point_list.Count（）;

for （int i = 0; i 《n; i++）

{

int IndexPre = （i - 1） % sum;

if （IndexPre == -1） IndexPre = sum - 1;

int IndexCurrent = i % sum;

int IndexNext = （i + 1） % sum;

var multiVal = multi（gSur_Point_list［IndexPre］.p， gSur_Point_list［IndexCurrent］.p， gSur_Point_list［IndexNext］.p）;

if （isCCW && multiVal》 0）

{

L1：

if （StackPoint.Count》 1）

{

var Top1Point = StackPoint.Pop（）;

var Top2Point = StackPoint.Peek（）;

multiVal = multi（Top2Point.p， Top1Point.p， gSur_Point_list［IndexCurrent］.p）;

if （isCCW && multiVal》 0）

StackPoint.Push（Top1Point）;

else

goto L1;

}

StackPoint.Push（gSur_Point_list［IndexCurrent］）;

}

}

return StackPoint.Reverse（）.ToList（）;

}

公共方法與數(shù)據(jù)結(jié)構(gòu)

/// 《summary》

/// Surface 坐標泛型集類 1

/// 《/summary》

public class gSur_Point

{

public gSur_Point（）

{ }

public gSur_Point（double x_val， double y_val， byte type_point_）

{

this.p.x = x_val;

this.p.y = y_val;

this.type_point = type_point_;

}

public gSur_Point（gPoint p， byte type_point_）

{

this.p = p;

this.type_point = type_point_;

}

public gPoint p;

/// 《summary》

/// 0 為折點 1 為順時針 2 為逆時針

/// 《/summary》

public byte type_point { get; set; } = 0;

/// 《summary》

/// 值

/// 《/summary》

public double Value { get; set; } = 0;

/// 《summary》

/// 角度

/// 《/summary》

public double Angle { get; set; } = 0;

/// 《summary》

/// 標記

/// 《/summary》

public bool isFalg { get; set; }

}

/// 《summary》

/// 點 數(shù)據(jù)類型 （XY）

/// 《/summary》

public struct gPoint

{

public gPoint（gPoint p_）

{

this.x = p_.x;

this.y = p_.y;

}

public gPoint（double x_val， double y_val）

{

this.x = x_val;

this.y = y_val;

}

public double x;

public double y;

public static gPoint operator +（gPoint p1， gPoint p2）

{

p1.x += p2.x;

p1.y += p2.y;

return p1;

}

public static gPoint operator -（gPoint p1， gPoint p2）

{

p1.x -= p2.x;

p1.y -= p2.y;

return p1;

}

public static gPoint operator +（gPoint p1， double val）

{

p1.x += val;

p1.y += val;

return p1;

}

public static bool operator ==（gPoint p1， gPoint p2）

{

return （p1.x == p2.x && p1.y == p2.y）;

}

public static bool operator ！=（gPoint p1， gPoint p2）

{

return ！（p1.x == p2.x && p1.y == p2.y）;

}

}

/// 《summary》

/// 求叉積 判斷［點 P 與線 L］ 位置關(guān)系［小于 0］ 在右邊 ［大于 0］ 在左邊 ［等于 0］ 共線

/// 《/summary》

/// 《param name=“ps”》《/param》

/// 《param name=“pe”》《/param》

/// 《param name=“p”》《/param》

/// 《returns》［小于 0］ 在右邊 ［大于 0］ 在左邊 ［等于 0］ 共線《/returns》

public double multi（gPoint ps， gPoint pe， gPoint p）

{

return （（ps.x - p.x） * （pe.y - p.y） - （pe.x - p.x） * （ps.y - p.y））;

}

/// 《summary》

/// 檢測 Surface 是否逆時針

/// 《/summary》

/// 《param name=“gSur_Point_list”》《/param》

/// 《returns》《/returns》

public bool s_isCCW（List《gSur_Point》 gSur_Point_list）

{

double d = 0;

int n = gSur_Point_list.Count（） - 1;

for （int i = 0; i 《n; i++）

{

if （gSur_Point_list.type_point》 0） continue;

int NextI = i + 1 + （gSur_Point_list［i + 1］.type_point》 0 ？ 1 ： 0）;

d += -0.5 * （gSur_Point_list［NextI］.p.y + gSur_Point_list.p.y） * （gSur_Point_list［NextI］.p.x - gSur_Point_list.p.x）;

}

return d》 0;

}

/// 《summary》

/// 返回兩點之間歐氏距離

/// 《/summary》

/// 《param name=“p1”》《/param》

/// 《param name=“p2”》《/param》

/// 《returns》《/returns》

public double p2p_di（gPoint p1， gPoint p2）

{

return Math.Sqrt（（p1.x - p2.x） * （p1.x - p2.x） + （p1.y - p2.y） * （p1.y - p2.y））;

}

/// 《summary》

/// 求方位角

/// 《/summary》

/// 《param name=“ps”》《/param》

/// 《param name=“pe”》《/param》

/// 《returns》《/returns》

public double p_ang（gPoint ps， gPoint pe）

{

double a_ang = Math.Atan（（pe.y - ps.y） / （pe.x - ps.x）） / Math.PI * 180;

// 象限角 轉(zhuǎn)方位角 計算所屬象限 并求得方位角

if （pe.x》= ps.x && pe.y》= ps.y） //↗ 第一象限

{

return a_ang;

}

else if （！（pe.x》= ps.x） && pe.y》= ps.y） // ↖ 第二象限

{

return a_ang + 180;

}

else if （！（pe.x》= ps.x） && ！（pe.y》= ps.y）） //↙ 第三象限

{

return a_ang + 180;

}

else if （pe.x》= ps.x && ！（pe.y》= ps.y）） // ↘ 第四象限

{

return a_ang + 360;

}

else

{

return a_ang;

}

}

View Code

三。 板邊凸點倒圓角方法

方法一。 也最簡單的倒角方法， 我們將 PCB 板邊凸點找出來后， 可以直接借助 genesis 倒角功能就可以實現(xiàn)了

當然但偶爾會報錯的， 且當 N 個小線段組成的尖角倒角會出錯（要實現(xiàn)完美效果只有自己寫倒角算法啦）

方法二： 自己寫倒角算法， 這個算法和加內(nèi)角孔算法類似 （這里只是介紹簡單的倒角） 考慮特殊的需要擴展

四。 凸點加倒圓角實現(xiàn)效果

編輯：hfy