古斯塔夫·基希霍夫(Gustav Kirchhoff)的電壓定律是我們可用于電路分析的第二個基本定律。他的電壓定律指出,對于閉環串聯路徑,電路中任何閉環周圍的所有電壓的代數和等于零。這是因為電路回路是閉合的導電路徑,因此不會損失任何能量。
換句話說,環路周圍所有電位差的代數和必須等于零,例如:ΣV= 0。在此注意,術語“代數和”是指考慮電源的極性和符號以及環路周圍的電壓降。
基爾霍夫(Kirchhoff)的想法通常被稱為能量守恒(Energy of Conservation),因為它在閉環或電路中移動,最終會回到電路中的起始位置,因此回到相同的初始電勢,而電路周圍沒有電壓損失。循環。因此,環路周圍的任何電壓降必須等于沿途遇到的任何電壓源。
因此,在將基爾霍夫電壓定律應用于特定電路元件時,重要的是我們要特別注意元件兩端的電壓降和源的電動勢的代數符號(+和-),否則我們的計算可能是錯誤的。
但是,在我們進一步仔細研究基爾霍夫電壓定律(KVL)之前,首先要了解單個元件(例如電阻器)上的壓降。
單回路元件
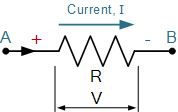
對于這個簡單的示例,我們將假定電流I與正電荷流(即常規電流)的方向相同。
在這里,流經電阻的電流從A點到B點,即從正極端子到負極端子。因此,當我們沿著與電流流動方向相同的方向行進時,電阻元件兩端的電位將下降,從而導致其兩端的-IR電壓降。
如果電流從B點到A點的方向相反,那么當我們從-電位轉變為+電位時,電阻元件兩端的電位會升高,從而給我們帶來+ I * R壓降。
因此,要將基爾霍夫電壓定律正確地應用于電路,我們必須首先了解極性的方向,并且如我們所見,跨阻性元件的電壓降的符號將取決于流過該元件的電流方向。通常,您將沿元件的相同電流方向釋放電勢,并隨著向電動勢源方向移動而獲得電勢。
可以假定閉合電路周圍的電流方向為順時針或逆時針,并且可以選擇其中一個。如果選擇的方向與電流的實際方向不同,則結果仍將是正確且有效的,但將導致代數答案的符號為負。
為了進一步理解這個想法,讓我們看一個電路回路,看看基爾霍夫的《電壓定律》是否成立。
單回路
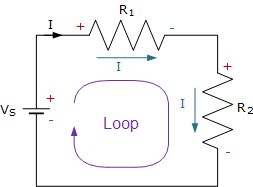
基爾霍夫(Kirchhoff)的電壓定律規定,任何環路中的電勢差的代數和必須等于零,例如:ΣV=0。由于兩個電阻R 1和R 2串聯連接在一起,因此它們都是電阻的一部分。相同的環路,因此相同的電流必須流經每個電阻器。
因此,電阻上的壓降R 1 = I * R 1,電阻上的壓降R 2 = I * R 2由KVL給出:
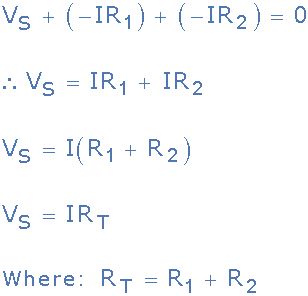
我們可以看到,將Kirchhoff的電壓定律應用于該單個閉環,可以得出串聯電路中等效或總電阻的公式,我們可以對此進行擴展以找到環路周圍的壓降值。
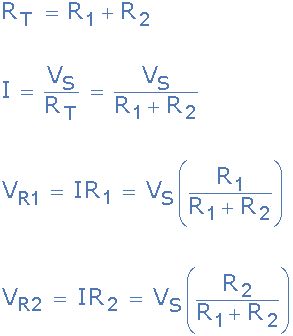
基爾霍夫電壓定律第1例
三個電阻值分別為10歐姆,20歐姆和30歐姆串聯連接在12伏電池電源上。計算:a)總電阻,b)電路電流,c)通過每個電阻器的電流,d)每個電阻器兩端的壓降,e)驗證基爾霍夫的電壓定律KVL成立。
a)總電阻(R T)
R T= R 1+ R 2+ R 3 =10Ω+20Ω+30Ω=60Ω
那么總電路電阻R T等于60Ω
b)電路電流(I)
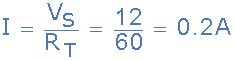
因此,總電路電流I等于0.2安培或200mA
c)每個電阻的電流
電阻串聯連接在一起,它們都是同一回路的一部分,因此每個電阻承受的電流量相同。從而:
I R1= I R2= I R3= I SERIES = 0.2安培
d)每個電阻兩端的壓降
V R1= I x R 1= 0.2 x 10 = 2伏
V R2= I x R 2= 0.2 x 20 = 4伏
V R3= I x R 3= 0.2 x 30 = 6伏
e)驗證基爾霍夫電壓定律
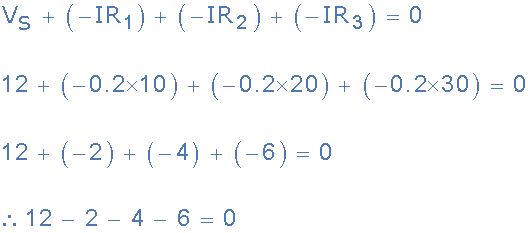
因此,基爾霍夫的電壓定律成立,因為閉環周圍的各個電壓降之和等于總電壓。
基爾霍夫的循環賽
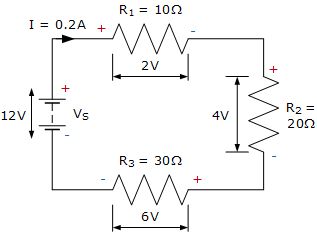
我們在這里已經看到基爾霍夫的電壓定律,KVL是基爾霍夫的第二定律,并指出了所有電壓降的代數和,即當您從某個固定點繞到閉合回路并返回到同一點時,并考慮了極性,始終為零。那就是ΣV= 0
基爾霍夫第二定律背后的理論也稱為電壓守恒定律,在處理串聯電路時,這對我們特別有用,因為串聯電路還充當分壓器,而分壓器電路是許多串聯的重要應用電路
責任編輯:lq
-
電路
+關注
關注
172文章
5852瀏覽量
171942 -
電流
+關注
關注
40文章
6765瀏覽量
131910 -
電壓定律
+關注
關注
0文章
3瀏覽量
2789
原文標題:基爾霍夫的電壓定律和能量守恒分析
文章出處:【微信號:A1411464185,微信公眾號:multisim】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 基爾霍夫的電壓定律和能量守恒分析
基爾霍夫的電壓定律和能量守恒分析










評論