本文講述了數(shù)據(jù)分析師應(yīng)當(dāng)了解的五個(gè)統(tǒng)計(jì)基本概念：統(tǒng)計(jì)特征、概率分布、降維、過采樣/欠采樣、貝葉斯統(tǒng)計(jì)方法。 從高的角度來看，統(tǒng)計(jì)學(xué)是一種利用數(shù)學(xué)理論來進(jìn)行數(shù)據(jù)分析的技術(shù)。象柱狀圖這種基本的可視化形式，會(huì)給你更加全面的信息。但是，通過統(tǒng)計(jì)學(xué)我們可以以更富有信息驅(qū)動(dòng)力和針對(duì)性的方式對(duì)數(shù)據(jù)進(jìn)行操作。所涉及的數(shù)學(xué)理論幫助我們形成數(shù)據(jù)的具體結(jié)論，而不僅僅是猜測(cè)。 利用統(tǒng)計(jì)學(xué)，我們可以更深入、更細(xì)致地觀察數(shù)據(jù)是如何進(jìn)行精確組織的，并且基于這種組織結(jié)構(gòu)，如何能夠以最佳的形式來應(yīng)用其它相關(guān)的技術(shù)以獲取更多的信息。今天，我們來看看數(shù)據(jù)分析師需要掌握的5個(gè)基本的統(tǒng)計(jì)學(xué)概念，以及如何有效地進(jìn)行應(yīng)用。 01特征統(tǒng)計(jì) 特征統(tǒng)計(jì)可能是數(shù)據(jù)科學(xué)中最常用的統(tǒng)計(jì)學(xué)概念。它是你在研究數(shù)據(jù)集時(shí)經(jīng)常使用的統(tǒng)計(jì)技術(shù)，包括偏差、方差、平均值、中位數(shù)、百分?jǐn)?shù)等等。理解特征統(tǒng)計(jì)并且在代碼中實(shí)現(xiàn)都是非常容易的。請(qǐng)看下圖：

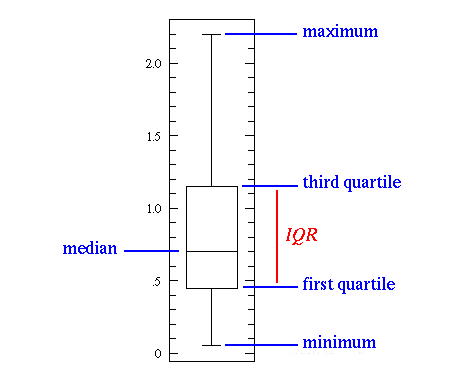
上圖中，中間的直線表示數(shù)據(jù)的中位數(shù)。中位數(shù)用在平均值上，因?yàn)樗鼘?duì)異常值更具有魯棒性。第一個(gè)四分位數(shù)本質(zhì)上是第二十五百分位數(shù)，即數(shù)據(jù)中的25%要低于該值。第三個(gè)四分位數(shù)是第七十五百分位數(shù)，即數(shù)據(jù)中的75%要低于該值。而最大值和最小值表示該數(shù)據(jù)范圍的上下兩端。 箱形圖很好地說明了基本統(tǒng)計(jì)特征的作用:

當(dāng)箱形圖很短時(shí)，就意味著很多數(shù)據(jù)點(diǎn)是相似的，因?yàn)楹芏嘀凳窃谝粋€(gè)很小的范圍內(nèi)分布;

當(dāng)箱形圖較高時(shí)，就意味著大部分的數(shù)據(jù)點(diǎn)之間的差異很大，因?yàn)檫@些值分布的很廣;

如果中位數(shù)接近了底部，那么大部分的數(shù)據(jù)具有較低的值。如果中位數(shù)比較接近頂部，那么大多數(shù)的數(shù)據(jù)具有更高的值。基本上，如果中位線不在框的中間，那么就表明了是偏斜數(shù)據(jù);

如果框上下兩邊的線很長(zhǎng)表示數(shù)據(jù)具有很高的標(biāo)準(zhǔn)偏差和方差，意味著這些值被分散了，并且變化非常大。如果在框的一邊有長(zhǎng)線，另一邊的不長(zhǎng)，那么數(shù)據(jù)可能只在一個(gè)方向上變化很大

02概率分布 我們可以將概率定義為一些事件將要發(fā)生的可能性大小，以百分?jǐn)?shù)來表示。在數(shù)據(jù)科學(xué)領(lǐng)域中，這通常被量化到0到1的區(qū)間范圍內(nèi)，其中0表示事件確定不會(huì)發(fā)生，而1表示事件確定會(huì)發(fā)生。那么，概率分布就是表示所有可能值出現(xiàn)的幾率的函數(shù)。請(qǐng)看下圖：

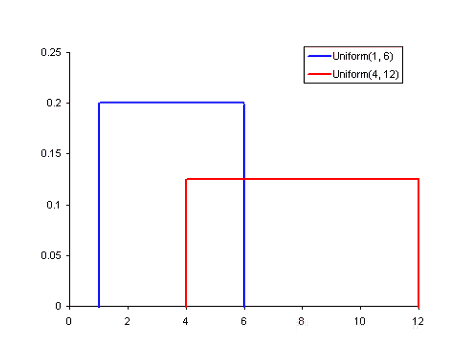
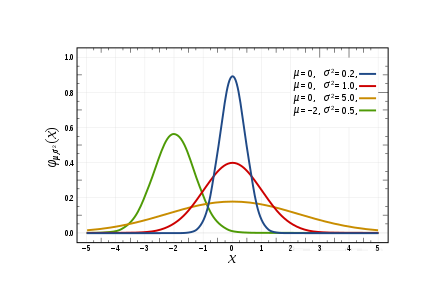
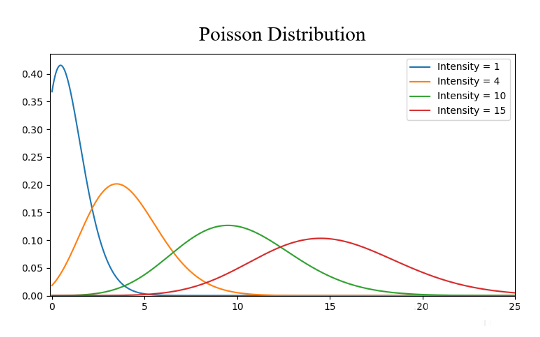
常見的概率分布，均勻分布(上)、正態(tài)分布(中間)、泊松分布(下)：

均勻分布是其中最基本的概率分布方式。它有一個(gè)只出現(xiàn)在一定范圍內(nèi)的值，而在該范圍之外的都是0。我們也可以把它考慮為是一個(gè)具有兩個(gè)分類的變量：0或另一個(gè)值。分類變量可能具有除0之外的多個(gè)值，但我們?nèi)匀豢梢詫⑵淇梢暬癁槎鄠€(gè)均勻分布的分段函數(shù)。

正態(tài)分布，通常也稱為高斯分布，具體是由它的平均值和標(biāo)準(zhǔn)偏差來定義的。平均值是在空間上來回變化位置進(jìn)行分布的，而標(biāo)準(zhǔn)偏差控制著它的分布擴(kuò)散范圍。與其它的分布方式的主要區(qū)別在于，在所有方向上標(biāo)準(zhǔn)偏差是相同的。因此，通過高斯分布，我們知道數(shù)據(jù)集的平均值以及數(shù)據(jù)的擴(kuò)散分布，即它在比較廣的范圍上擴(kuò)展，還是主要圍繞在少數(shù)幾個(gè)值附近集中分布。

泊松分布與正態(tài)分布相似，但存在偏斜率。象正態(tài)分布一樣，在偏斜度值較低的情況下，泊松分布在各個(gè)方向上具有相對(duì)均勻的擴(kuò)散。但是，當(dāng)偏斜度值非常大的時(shí)候，我們的數(shù)據(jù)在不同方向上的擴(kuò)散將會(huì)是不同的。在一個(gè)方向上，數(shù)據(jù)的擴(kuò)散程度非常高，而在另一個(gè)方向上，擴(kuò)散的程度則非常低。

如果遇到一個(gè)高斯分布，那么我們知道有很多算法，在默認(rèn)情況下高思分布將會(huì)被執(zhí)行地很好，因此首先應(yīng)該找到那些算法。如果是泊松分布，我們必須要特別謹(jǐn)慎，選擇一個(gè)在空間擴(kuò)展上對(duì)變化要有很好魯棒性的算法。 03降維 降維這個(gè)術(shù)語可以很直觀的理解，意思是降低一個(gè)數(shù)據(jù)集的維數(shù)。在數(shù)據(jù)科學(xué)中，這是特征變量的數(shù)量。請(qǐng)看下圖：

上圖中的立方體表示我們的數(shù)據(jù)集，它有3個(gè)維度，總共1000個(gè)點(diǎn)。以現(xiàn)在的計(jì)算能力，計(jì)算1000個(gè)點(diǎn)很容易，但如果更大的規(guī)模，就會(huì)遇到麻煩了。然而，僅僅從二維的角度來看我們的數(shù)據(jù)，比如從立方體一側(cè)的角度，可以看到劃分所有的顏色是很容易的。通過降維，我們將3D數(shù)據(jù)展現(xiàn)到2D平面上，這有效地把我們需要計(jì)算的點(diǎn)的數(shù)量減少到100個(gè)，大大節(jié)省了計(jì)算量。 另一種方式是我們可以通過特征剪枝來減少維數(shù)。利用這種方法，我們刪除任何所看到的特征對(duì)分析都不重要。例如，在研究數(shù)據(jù)集之后，我們可能會(huì)發(fā)現(xiàn)，在10個(gè)特征中，有7個(gè)特征與輸出具有很高的相關(guān)性，而其它3個(gè)則具有非常低的相關(guān)性。那么，這3個(gè)低相關(guān)性的特征可能不值得計(jì)算，我們可能只是能在不影響輸出的情況下將它們從分析中去掉。 用于降維的最常見的統(tǒng)計(jì)技術(shù)是PCA，它本質(zhì)上創(chuàng)建了特征的向量表示，表明了它們對(duì)輸出的重要性，即相關(guān)性。PCA可以用來進(jìn)行上述兩種降維方式的操作。 04過采樣和欠采樣 過采樣和欠采樣是用于分類問題的技術(shù)。例如，我們有1種分類的2000個(gè)樣本，但第2種分類只有200個(gè)樣本。這將拋開我們嘗試和使用的許多機(jī)器學(xué)習(xí)技術(shù)來給數(shù)據(jù)建模并進(jìn)行預(yù)測(cè)。那么，過采樣和欠采樣可以應(yīng)對(duì)這種情況。請(qǐng)看下圖：

在上面圖中的左右兩側(cè)，藍(lán)色分類比橙色分類有更多的樣本。在這種情況下，我們有2個(gè)預(yù)處理選擇，可以幫助機(jī)器學(xué)習(xí)模型進(jìn)行訓(xùn)練。 欠采樣意味著我們將只從樣本多的分類中選擇一些數(shù)據(jù)，而盡量多的使用樣本少的分類樣本。這種選擇應(yīng)該是為了保持分類的概率分布。我們只是通過更少的抽樣來讓數(shù)據(jù)集更均衡。 過采樣意味著我們將要?jiǎng)?chuàng)建少數(shù)分類的副本，以便具有與多數(shù)分類相同的樣本數(shù)量。副本將被制作成保持少數(shù)分類的分布。我們只是在沒有獲得更多數(shù)據(jù)的情況下讓數(shù)據(jù)集更加均衡。 05貝葉斯統(tǒng)計(jì) 完全理解為什么在我們使用貝葉斯統(tǒng)計(jì)的時(shí)候，要求首先理解頻率統(tǒng)計(jì)失敗的地方。大多數(shù)人在聽到“概率”這個(gè)詞的時(shí)候，頻率統(tǒng)計(jì)是首先想到的統(tǒng)計(jì)類型。它涉及應(yīng)用一些數(shù)學(xué)理論來分析事件發(fā)生的概率，明確地說，我們唯一計(jì)算的數(shù)據(jù)是先驗(yàn)數(shù)據(jù)(prior data)。

假設(shè)我給了你一個(gè)骰子，問你擲出6點(diǎn)的幾率是多少，大多數(shù)人都會(huì)說是六分之一。 但是，如果有人給你個(gè)特定的骰子總能擲出6個(gè)點(diǎn)呢?因?yàn)轭l率分析僅僅考慮之前的數(shù)據(jù)，而給你作弊的骰子的因素并沒有被考慮進(jìn)去。 貝葉斯統(tǒng)計(jì)確實(shí)考慮了這一點(diǎn)，我們可以通過貝葉斯法則來進(jìn)行說明:

在方程中的概率P(H)基本上是我們的頻率分析，給定之前的關(guān)于事件發(fā)生概率的數(shù)據(jù)。方程中的P(E|H)稱為可能性，根據(jù)頻率分析得到的信息，實(shí)質(zhì)上是現(xiàn)象正確的概率。例如，如果你要擲骰子10000次，并且前1000次全部擲出了6個(gè)點(diǎn)，那么你會(huì)非常自信地認(rèn)為是骰子作弊了。 如果頻率分析做的非常好的話，那么我們會(huì)非常自信地確定，猜測(cè)6個(gè)點(diǎn)是正確的。同時(shí)，如果骰子作弊是真的，或者不是基于其自身的先驗(yàn)概率和頻率分析的，我們也會(huì)考慮作弊的因素。正如你從方程式中看到的，貝葉斯統(tǒng)計(jì)把一切因素都考慮在內(nèi)了。當(dāng)你覺得之前的數(shù)據(jù)不能很好地代表未來的數(shù)據(jù)和結(jié)果的時(shí)候，就應(yīng)該使用貝葉斯統(tǒng)計(jì)方法。

責(zé)任編輯：xj

原文標(biāo)題：5個(gè)基本概念，從統(tǒng)計(jì)學(xué)到機(jī)器學(xué)習(xí)

文章出處：【微信公眾號(hào)：深度學(xué)習(xí)自然語言處理】歡迎添加關(guān)注！文章轉(zhuǎn)載請(qǐng)注明出處。