使用 MNIST 數(shù)據(jù)集對 0 到 9 之間的數(shù)字進行手寫數(shù)字識別是神經(jīng)網(wǎng)絡的一個典型入門教程。
該技術在現(xiàn)實場景中是很有用的,比如可以把該技術用來掃描銀行轉帳單或支票,其中帳號和需要轉賬的金額可以被識別處理并寫在明確定義的方框中。
在本教程中,我們將介紹如何使用 Julia 編程語言和名為 Flux 的機器學習庫來實現(xiàn)這一技術。為什么使用 Flux 和 Julia?本教程為什么想使用 Flux(https://fluxml.ai/) 和 Julia(https://julialang.org/) ,而不是像 Torch、PyTorch、Keras 或 TensorFlow 2.0 這樣的知名框架呢?一個很好的原因是因為 Flux 更易于學習,而且它提供更好的性能和擁有有更大的潛力,另外一個原因是,Flux 在仍然是一個小庫的情況下實現(xiàn)了很多功能。Flux 庫非常小,因為它所做的大部分工作都是由 Julia 編程語言本身提供的。例如,如果你查看 Gorgonia ML 庫(https://github.com/gorgonia/gorgonia) 中的 Go 編程語言,你將看到,它明確地展示了其他機器學習庫如何構建一個需要執(zhí)行和區(qū)分的表達式圖。在 Flux 中,這個圖就是 Julia 本身。Julia 與 LISP 非常相似,因為 Julia 代碼可以很容易地表示為數(shù)據(jù)結構,可以對其進行修改和計算。機器學習概論如果你是機器學習的新手,你可以跟著本教程來學習,但并不是所有的東西對你來說都是有價值的。你也可以看看我以前關于 Medium 的一些文章,它們可能會解釋你一些新手的疑惑:線性代數(shù)的核心思想。(https://medium.com/@Jernfrost/the-core-idea-of-linear-algebra-7405863d8c1d)線性代數(shù)基本上是關于向量和矩陣的,這是你在機器學習中經(jīng)常用到的東西。使用引用。(https://medium.com/@Jernfrost/working-with-and-emulating-references-in-julia-e02c1cae5826)它看起來有點不太好理解,但是如果你想理解像 Flux 這樣的 ML 庫,那么理解 Julia 中的引用是很重要的。Flux 的實現(xiàn)。(https://medium.com/@Jernfrost/implementation-of-a-modern-machine-learning-library-3596badf3be)如何實現(xiàn) Flux-ML 庫的初學者指南。機器學習簡介。(https://medium.com/@Jernfrost/machine-learning-for-dummies-in-julia-6cd4d2e71a46) 機器學習概論。簡單多層感知機我們要編程的人工神經(jīng)網(wǎng)絡被稱為簡單的多層感知機,這是神經(jīng)網(wǎng)絡(ANN)的基礎,大多數(shù)教科書都會從它開始。我先展示整個程序,然后我們再更詳細地講解不同的部分。using Flux, Flux.Data.MNIST, Statistics
using Flux: onehotbatch, onecold, crossentropy, throttle
using Base.Iterators: repeated
# Load training data. 28x28 grayscale images of digits
imgs = MNIST.images()
# Reorder the layout of the data for the ANN
imagestrip(image::Matrix{<:Gray}) = Float32.(reshape(image, :))
X = hcat(imagestrip.(imgs)...)
# Target output. What digit each image represents.
labels = MNIST.labels()
Y = onehotbatch(labels, 0:9)
# Defining the model (a neural network)
m = Chain(
Dense(28*28, 32, relu),
Dense(32, 10),
softmax)
loss(x, y) = crossentropy(m(x), y)
dataset = repeated((X, Y), 200)
opt = ADAM()
evalcb = () -> @show(loss(X, Y))
# Perform training on data
Flux.train!(loss, params(m), dataset, opt, cb = throttle(evalcb, 10))
探索輸入數(shù)據(jù)數(shù)據(jù)預處理通常是數(shù)據(jù)科學中最大的工作之一。通常情況下,數(shù)據(jù)的組織或格式化方式與將其輸入算法所需的方式不同。我們首先將 MNIST 數(shù)據(jù)集加載為 60000 個 28x28 像素的灰度圖像:imgs = MNIST.images()
現(xiàn)在,如果你這樣處理數(shù)據(jù),你可能不知道輸出的數(shù)據(jù)是怎么樣子的,但使用 Julia 研究,我們只需檢查一下:julia> size(imgs)
(60000,)
輸出說明了 imgs 是一個包含 60000 個元素的一維數(shù)組。但這些元素是什么?julia> eltype(imgs)
Array{Gray{FixedPointNumbers.Normed{UInt8,8}},2}
你可能看不懂,但我可以簡單地告訴你這是什么:julia> eltype(imgs) <: Matrix{T} where T <: Gray
true
這告訴我們 imgs 中的每個元素都是某種值矩陣,這些值屬于某種類型 T,它是 Gray 類型的子類型。什么是 Gray 類型?我們可以在 Julia 在線文檔中查找:help?> Gray
Gray is a grayscale object. You can extract its value with gray(c).
如果我們想知道這些灰度值矩陣的維數(shù),則可以:julia> size(imgs[1])
(28, 28)
julia> size(imgs[2])
(28, 28)
這告訴我們它們的尺寸為 28x28 像素。我們可以通過簡單地繪制其中的一些圖來進一步驗證這一點。Julia 的 Plots 庫使你可以繪制函數(shù)和圖像。julia> using Plots
julia> plot(imgs[2])
但是,你可能會發(fā)現(xiàn)了解更多的數(shù)據(jù)看起來是更有用。我們可以很容易地一起繪制幾個圖像:imgplots = plot.(imgs[1:9])
plot(imgplots...)
現(xiàn)在我們知道了數(shù)據(jù)是什么樣的了。準備輸入數(shù)據(jù)然而,我們不能像這樣將數(shù)據(jù)輸入到我們的神經(jīng)網(wǎng)絡(ANN),因為每個神經(jīng)網(wǎng)絡輸入必須是列向量,而不是矩陣。這是因為神經(jīng)網(wǎng)絡期望一個矩陣作為輸入,矩陣中的每一列都是輸入。ANN 所看到的三乘十矩陣對應于十個不同的輸入,其中每個輸入包含三個不同的值或者更具體地說是三個不同的特征,因此,我們將 28x28 灰度圖像轉換為 28x28=784 的長像素帶。其次,我們的神經(jīng)網(wǎng)絡并不知道什么是灰度值,它是對浮點數(shù)據(jù)進行操作的,所以我們必須同時轉換數(shù)據(jù)的維度和元素類型。數(shù)組中的列和行數(shù)稱為其形狀。很多人提到了張量,雖然它并不完全精確,但它是一個涵蓋了標量、向量、矩陣、立方體或任何等級的數(shù)組(基本上是數(shù)組的所有維度)的概念。在 Julia 中,我們可以使用 reshape 函數(shù)來改變數(shù)組的形狀。下面是一些你如何使用它的例子。這將創(chuàng)建一個包含四個元素的列向量 A:julia> A = collect(1:4)
4-element Array{Int64,1}:
1
2
3
4
通過 reshape 我們把它變成一個二乘二的矩陣 B:julia> B = reshape(A, (2, 2))
2×2 Array{Int64,2}:
1 3
2 4
矩陣可以再次轉換為列向量:julia> reshape(B, 4)
4-element Array{Int64,1}:
1
2
3
4
找出一個列向量到底有多少個元素是不切實際的,你可以讓 Julia 只通過寫來計算合適的長度。julia> reshape(B, :)
4-element Array{Int64,1}:
1
2
3
4
有了這些信息,應該更容易看到 imagestrip 函數(shù)的實際功能了,它將 28x28 的灰度矩陣轉換為 784 個 32 位浮點值的列向量。imagestrip(image::Matrix{<:Gray}) = Float32.(reshape(image, :))
該.符號用于將函數(shù)應用于數(shù)組的每個元素,因此 Float32.(xs)與 map(Float32, xs)是相同的。接下來,我們將 imagestrip 函數(shù)應用于 6 萬張灰度圖像中的每一張,生成 784x6000 個輸入矩陣 X。X = hcat(imagestrip.(imgs)...)
這是如何運作的?可以想象為 imagestrip.(imgs)將圖像轉換為單個輸入值的數(shù)組,例如[X?, X?, X?, ..., X?],其中 n = 60,000,每個 X?都是 784 個浮點值。使用 splat 運算符...,我們將其轉換為所有這些列向量的水平連接,以產(chǎn)生模型輸入。X = hcat(X?, X?, X?, ..., X?)
如果要驗證尺寸,則可以運行 size(X)。接下來,我們加載標簽。labels = MNIST.labels()
標簽是我們稱之為監(jiān)督學習中觀察的"答案"部分。在我們的任務中,標簽是從 0 到 9 的數(shù)字。手繪數(shù)字的每一個圖像都應歸類為十個不同的數(shù)字之一,例如,如果這是一個包含不同花卉品種的花瓣長度和花瓣寬度的虹膜數(shù)據(jù)集,那么該品種的名稱就是標簽。X?代表我們所有的特征向量,用機器學習的術語來說,每個像素的灰度值都是一個特征。你可以將標簽與我們繪制的圖像進行比較。imgplots = plot.(imgs[1:9])
plot(imgplots...)
labels[1:9]
獨熱編碼每個圖像一個標簽,則有 60000 個標簽,然而神經(jīng)網(wǎng)絡不能直接輸出標簽。例如,如果你正試圖對貓和狗的圖像進行分類,那么一個網(wǎng)絡不能輸出字符串“dog”或“cat”,因為它是使用浮點值的。如果標簽是一個不一定有用的數(shù)字,例如如果輸出是一系列郵政編碼,那么將 3000 的郵政編碼視為 1500 的郵政編碼的兩倍是沒有意義的,同樣,當使用神經(jīng)網(wǎng)絡從圖像中預測數(shù)字時,4 的大小是 2 的兩倍并不重要,數(shù)字也可能是字母,因此它們的值不重要。我們在機器學習中處理這個問題的方法是使用所謂的獨熱編碼,這意味著,如果我們有標簽 A、B 和 C,并且我們想用獨熱編碼來表示它們,那么 A 是[1、0、0],B 是[0、1、0],C 是[0、0、1]。這看起來很浪費空間,但在 Julia one hot 數(shù)組內部,它只跟蹤元素的索引,并不保存所有的零。下面是一些正在使用的編碼示例:julia> Flux.onehot('B', ['A', 'B', 'C'])
3-element Flux.OneHotVector:
0
1
0
julia> Flux.onehot("foo", ["foo", "bar", "baz"])
3-element Flux.OneHotVector:
1
0
0
但是,我們不會使用 onehot 函數(shù),因為我們正在創(chuàng)建一批獨熱編碼標簽,我們將把 60000 張圖片作為一個批次來處理。機器學習的批次指的是在我們模型(神經(jīng)網(wǎng)絡)的權值或參數(shù)更新之前必須完成的最小樣本數(shù)量。Y = onehotbatch(labels, 0:9)
這將創(chuàng)建目標輸出。在理想情況下,模型(X)==Y,但在現(xiàn)實中,即使經(jīng)過模型的訓練,也會有一些偏差。我們已經(jīng)討論完數(shù)據(jù)準備,現(xiàn)在讓我們用人工神經(jīng)網(wǎng)絡來構造我們的模型。構造神經(jīng)網(wǎng)絡模型模型是真實世界的簡化表示,就像我們可以建立簡化的物理模型一樣,我們也可以用數(shù)學或代碼來創(chuàng)建物理世界的模型,現(xiàn)實中存在許多這樣的數(shù)學模型。例如,統(tǒng)計模型可以使用統(tǒng)計數(shù)據(jù)來模擬人們一天中是如何到達商店的。一般來說,人們會以一種遵循特定概率分布的方式到達。在我們的例子中,我們試圖用神經(jīng)網(wǎng)絡來模擬現(xiàn)實世界中的一些東西,當然,這只是對現(xiàn)實世界的一種近似。當我們建立一個神經(jīng)網(wǎng)絡時,我們有很多可以玩的東西。網(wǎng)絡是由多個層連接而成的,每一層通常都有一個激活函數(shù)。建立一個神經(jīng)網(wǎng)絡的挑戰(zhàn)是選擇合適的層和激活函數(shù),并決定每層應該有多少個節(jié)點。我們的模型非常簡單,定義如下:m = Chain(
Dense(28^2, 32, relu),
Dense(32, 10),
softmax)
這是一個三層的神經(jīng)網(wǎng)絡。Chain 用于將各個層連接在一起。第一層 Dense(28^2, 32, relu)有 784(28x28)個輸入節(jié)點,對應于每個圖像中的像素數(shù)。它使用校正線性單元(ReLU)函數(shù)作為激活函數(shù)。在經(jīng)典的神經(jīng)網(wǎng)絡文獻中,通常會介紹 sigmoid 和 tanh。relu 等激活函數(shù),這些激活函數(shù)在大多數(shù)情況下都工作得很好,包括圖像的分類。下一層是我們的隱藏層,它接受 32 個輸入,因為前一層有 32 個輸出,隱藏節(jié)點的數(shù)量沒有明確的對錯選擇。但輸出的數(shù)量根據(jù)不同任務是不一樣的,因為我們希望每個數(shù)字有一個輸出,這也就是“獨熱編碼”發(fā)揮作用的地方。Softmax 函數(shù)最后一層,是 softmax 函數(shù),它以前一層的輸出的矩陣作為輸入,并沿著每一列進行歸一化。標準化將 60000 列中的每一列轉換為概率分布。那到底是什么意思?概率是 0 到 1 之間的值,0 表示事件永遠不會發(fā)生,1 是肯定會發(fā)生。與 min-max 歸一化一樣,softmax 將所有輸入歸一化為 0 到 1 之間的值,但是與 min max 不同的是它會確保所有值的和為一。這需要一些例子來說明。假設我創(chuàng)建了 10 個從 1 到 10 的隨機值,我們可以放任意范圍和任意數(shù)量的值。julia> ys = rand(1:10, 10)
10-element Array{Int64,1}:
9
6
10
5
10
2
6
6
7
9
現(xiàn)在讓我們使用不同的歸一化函數(shù)歸一化這個數(shù)組,我們將使用來自 LinearAlgebra 模塊的 normalize,因為它與 Julia 捆綁在一起。但首先使用 softmax:julia> softmax(ys)
10-element Array{Float64,1}:
0.12919082661651196
0.006432032517257137
0.3511770763952676
0.002366212528045101
0.3511770763952676
0.00011780678490667763
0.006432032517257137
0.006432032517257137
0.017484077111717768
0.12919082661651196
如你所見,所有值都在 0 到 1 之間。現(xiàn)在看一下如果我們把它們加起來會發(fā)生什么:julia> sum(softmax(ys))
0.9999999999999999
它們基本上變成了 1。現(xiàn)在將其與 normalize 的功能進行對比:julia> using LinearAlgebra
julia> normalize(ys)
10-element Array{Float64,1}:
0.38446094597254243
0.25630729731502827
0.4271788288583805
0.21358941442919024
0.4271788288583805
0.0854357657716761
0.25630729731502827
0.25630729731502827
0.2990251802008663
0.38446094597254243
julia> sum(normalize(ys))
2.9902518020086633
julia> norm(normalize(ys))
1.0
julia> norm(softmax(ys))
0.52959100847191
如果對用 normalize 歸一化的值求和,它們只會得到一些隨機值,然而如果我們把結果反饋給 norm,我們得到的結果正好是 1.0。不同之處在于,normalize 將向量中的值進行了歸一化,以便它們可以表示單位向量,即長度正好為一的向量。norm 給出向量的大小。相比之下,softmax 不會將這些值視為向量,而是將其視為概率分布,每個元素表示輸入圖像為該數(shù)字的概率。假設我們有 A,B 和 C 的圖像作為輸入,如果你從 softmax 得到一個輸出值是[0.1,0.7,0.2],那么輸入圖像有 10%的可能性是 A 的圖形,有 70%的可能性是 B 的圖形,最后有 20%的可能性是 C 的圖形。這就是為什么我們希望 softmax 作為最后一層的原因。用神經(jīng)網(wǎng)絡不能絕對確定輸入圖像是什么,但是我們可以給出一個概率分布,它表示更有可能是哪個數(shù)字。定義損失函數(shù)當訓練我們的神經(jīng)網(wǎng)絡(模型)給出準確的預測時,我們需要定義人工神經(jīng)網(wǎng)絡(ANN)的評估指標。為此,我們使用所謂的損失函數(shù)。損失函數(shù)有很多名字,20 年前當我被教授神經(jīng)網(wǎng)絡時,我們曾稱之為誤差函數(shù),也有人稱之為成本函數(shù)。然而,歸根結底,這是一種表達我們的預測與現(xiàn)實相比有多正確的方式。loss(x, y) = crossentropy(m(x), y)
訓練神經(jīng)網(wǎng)絡實際上是最小化這個函數(shù)的輸出,所以這是一個優(yōu)化問題。訓練是一個反復調整模型中參數(shù)(權重)的過程,直到損失函數(shù)的輸出變低,或者換句話說,直到我們的預測誤差變低。均方誤差函數(shù)(MSE)是計算預測錯誤程度的經(jīng)典方法,這就意味著取差的平方,然而,MSE 更適合于線性回歸(將一條或多條直線擬合到某些觀測值)。在這種情況下,我們改用交叉熵函數(shù)。當你的最后一層是 softmax,進行分類而不是線性回歸時,這是我比較推薦的選擇。指定 Epoch 在機器學習術語中,Epoch 是訓練算法進行一次完整的迭代,換句話說:一個 Epoch 處理一個批次并更新權重因此,如果我們使用 10 個 Epoch 來進行訓練,那么模型的參數(shù) / 權重將更新 / 調整 10 次。為了得到 200 個 Epoch,我們使用 repeat 重復我們的批處理 200 次。它實際上不會重復我們的數(shù)據(jù) 200 次,它只是用迭代器創(chuàng)建了這樣的錯覺。dataset = repeated((X, Y), 200)
在數(shù)據(jù)集中,我們得到的數(shù)組如下:dataset = [(X1, Y1), (X2, Y2), ..., (X200, Y200)]
優(yōu)化器最常見和最著名的訓練神經(jīng)網(wǎng)絡策略是梯度下降算法,這是由 Julia 中的 Descent 類型提供的。然而,在我們的例子中,當我們處理大量帶有相當數(shù)量噪聲的數(shù)據(jù)時,建議改用 ADAM 優(yōu)化器,這就是所謂的隨機優(yōu)化。opt = ADAM()
進行訓練我們終于可以進行訓練了,但我們希望在訓練進行的過程中得到一些反饋。我們定義了一個回調函數(shù),在每次迭代(epoch)時,它將輸出 loss 函數(shù)的值,從而顯示錯誤。我們希望每次迭代時都能看到這個錯誤。evalcb = () -> @show(loss(X, Y))
觀察錯誤發(fā)展的一個有用的地方是,你可以看到是否有振蕩。人工神經(jīng)網(wǎng)絡過快地朝著最低值過渡,會導致它朝相反的方向移動,如果速度太快,則會向相反的方向超調,振蕩會變得更加劇烈,直到誤差變?yōu)闊o窮大。這是一個切換優(yōu)化算法或降低學習率的提示。不管怎樣,這就是你訓練的方式。注意,回調是可選的:Flux.train!(loss, params(m), dataset, opt, cb = throttle(evalcb, 10))
評價模型預測精度經(jīng)過訓練后,我們可以測試模型在預測方面的表現(xiàn)。我們定義了這樣一個函數(shù):accuracy(x, y) = mean(onecold((m(x))) .== onecold(y))
然后我們用輸入數(shù)據(jù)和標簽作為輸入?yún)?shù)來調用它:@show accuracy(X, Y)
至于什么是 onecold?在某種程度上,它與 onehot 實現(xiàn)的效果是相反的。我們的輸出 m(X)都是概率分布,而我們的目標 Y 都是獨熱向量。它們不能直接比較,所以我們需要使用 onecold 來做一個轉換。給定概率分布,它選擇最可能的候選:julia> onecold([0.1, 0.7, 0.2])
2
julia> onecold([0.9, 0.05, 0.05])
1
因此,使用 onecold(m(X))我們可以得到預測的標簽,這可以與實際的標簽 onecold(y)進行比較。用測試數(shù)據(jù)驗證模型到目前為止,我們只根據(jù)我們使用的訓練數(shù)據(jù)來驗證了我們的模型,然而,如果該模型不適用于新的數(shù)據(jù),它將是完全無用的。因此,在訓練網(wǎng)絡時,我們通常將數(shù)據(jù)分為訓練數(shù)據(jù)和測試數(shù)據(jù)。測試數(shù)據(jù)不是訓練的一部分,只有在訓練完成后才能進行測試。tX = hcat(float.(reshape.(MNIST.images(:test), :))...)
tY = onehotbatch(MNIST.labels(:test), 0:9)
@show accuracy(tX, tY)
最后我希望這能幫助你理解建立神經(jīng)網(wǎng)絡的過程。太多的教程傾向于跳過向初學者解釋的內容,從而所有的新概念都會很快變得令人困惑。我希望這為初學者在進一步探索機器學習之前提供了一個起點,特別是基于 Julia 的機器學習,因為我認為 Julia 有著光明的未來。
審核編輯 黃昊宇
-
神經(jīng)網(wǎng)絡
+關注
關注
42文章
4762瀏覽量
100540 -
數(shù)字識別
+關注
關注
2文章
19瀏覽量
10135 -
python
+關注
關注
56文章
4782瀏覽量
84453 -
FLUX
+關注
關注
0文章
3瀏覽量
5714
發(fā)布評論請先 登錄
相關推薦
使用Python卷積神經(jīng)網(wǎng)絡(CNN)進行圖像識別的基本步驟
【PYNQ-Z2申請】基于PYNQ-Z2的神經(jīng)網(wǎng)絡圖形識別
【PYNQ-Z2試用體驗】神經(jīng)網(wǎng)絡基礎知識
【PYNQ-Z2試用體驗】基于PYNQ-Z2的神經(jīng)網(wǎng)絡圖形識別[結項]
人工神經(jīng)網(wǎng)絡手寫數(shù)字識別系統(tǒng)的詳細資料概述
谷歌向神經(jīng)網(wǎng)絡手寫數(shù)字識別發(fā)起挑戰(zhàn),竟用量子計算識別

使用PyhonFluxJulia實現(xiàn)手寫數(shù)字識別的神經(jīng)網(wǎng)絡入門教程
用Python從頭實現(xiàn)一個神經(jīng)網(wǎng)絡來理解神經(jīng)網(wǎng)絡的原理1
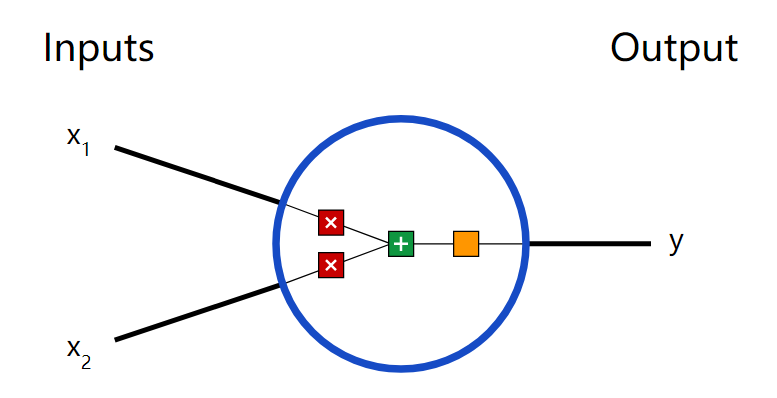
用Python從頭實現(xiàn)一個神經(jīng)網(wǎng)絡來理解神經(jīng)網(wǎng)絡的原理2
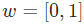
用Python從頭實現(xiàn)一個神經(jīng)網(wǎng)絡來理解神經(jīng)網(wǎng)絡的原理3

用Python從頭實現(xiàn)一個神經(jīng)網(wǎng)絡來理解神經(jīng)網(wǎng)絡的原理4





 神經(jīng)網(wǎng)絡入門:使用Python+Flux+Julia來實現(xiàn)手寫數(shù)字識別
神經(jīng)網(wǎng)絡入門:使用Python+Flux+Julia來實現(xiàn)手寫數(shù)字識別










評論