復(fù)數(shù)最直觀的理解就是旋轉(zhuǎn)!
4*i*i = -4
就是“4”在數(shù)軸上旋轉(zhuǎn)了 180 度。
那么 4*i 就是旋轉(zhuǎn)了 90 度。
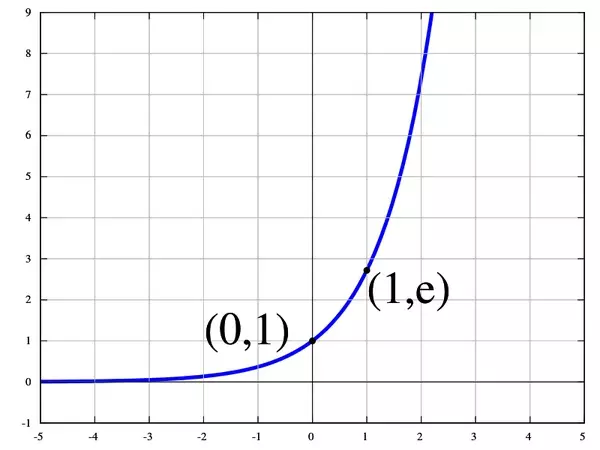
另外,e^t 是什么樣呢?
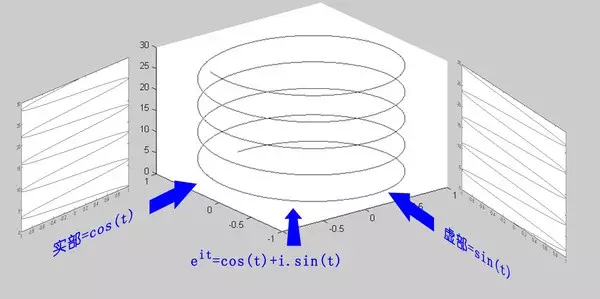
但當(dāng)你在指數(shù)上加上 i 之后呢?
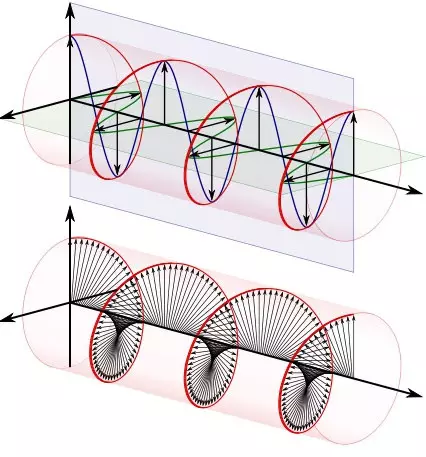
變成了一個螺旋線。是不是和電磁場很像?(想拿歐拉公式去跟女生炫學(xué)術(shù)的男生注意了:她們,真的,不 CARE)
當(dāng)然,更重要的意義在于復(fù)數(shù)運(yùn)算保留了二維信息。
假如我讓你計算 3+5,雖然你可以輕松的計算出 8,但是如果讓你分解 8 你會有無數(shù)種分解的方法,3 和 5 原始在各自維度上的信息被覆蓋了。
但是計算 3+5i 的話,你依然可以分解出實(shí)部和虛部,就像上圖那樣。
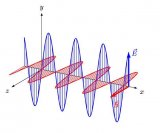
基于以上兩個理由,用復(fù)數(shù)來描述電場與磁場簡直完美到爆棚!
我們即可以讓電場強(qiáng)度與復(fù)數(shù)磁場強(qiáng)度相加而不損失各自的信息,又滿足了電場與磁場 90 度垂直的要求。另外,一旦我們需要讓任何一個場旋轉(zhuǎn) 90 度,只要乘一個“i”就可以了
補(bǔ)充一點(diǎn):
正弦波在頻域可以看作是自然數(shù)中的“1”,可以構(gòu)成其他數(shù)字的基礎(chǔ)元素。當(dāng)你需要 5 的時候,你可以看成是 1*5(基礎(chǔ)元素的五倍)也看以看成 2+3(一個基礎(chǔ)元素 2 倍與基礎(chǔ)元素 3 倍的和)。這些用基礎(chǔ)元素構(gòu)成新元素的運(yùn)算是線性運(yùn)算。
但是現(xiàn)在你如何用線性運(yùn)算吧 2sin(wt)變換成 4sin(wt+pi/6)呢?
利用歐拉公式,我們可以將任何一個正弦波看作其在實(shí)軸上的投影。假如兩個不同的正弦波,可以用數(shù)學(xué)表達(dá)為:
好了,現(xiàn)在如果我想用第一個正弦波利用線性變換為第二個,我們就只需要將 A 乘對應(yīng)的系數(shù)使其放大至 B(本例為乘 2),然后將θ1 加上一定的角度使其變?yōu)棣?(本例為加 30 度),然后將得到的第二個虛數(shù)重新投影回實(shí)軸,就完成了在實(shí)數(shù)中完全無法做到的變換。
這種利用復(fù)指數(shù)來計算正弦波的方法也對電磁波極其適用,因?yàn)殡姶挪ǘ际钦也ǎ?dāng)我們需要一個電磁波在時間上延遲 / 提前,或是在空間上前移 / 后移,只需要乘一個復(fù)指數(shù)就可以完成對相位的調(diào)整了。
-
電磁場
+關(guān)注
關(guān)注
0文章
790瀏覽量
47232 -
電場強(qiáng)度
+關(guān)注
關(guān)注
0文章
11瀏覽量
7391
發(fā)布評論請先 登錄
相關(guān)推薦
交流電與電磁波的關(guān)系
哪種物質(zhì)可以屏蔽電磁波
密閉的金屬容器屏蔽電磁波原理是什么
為什么金屬可以屏蔽電磁波的原因
毫米波雷達(dá)是聲波還是電磁波
雷達(dá)水位監(jiān)測的原理是基于電磁波的反射和傳播特性
基于電磁波的遙感系統(tǒng)
電磁波輻射測試儀怎么使用
電磁屏蔽技術(shù)的原理解析
電磁波是什么的電流
為什么電磁波具有光粒二象性?
電磁波如何探測?
為什么電磁波的頻率范圍要比聲波寬廣?
三大電磁場仿真軟件有哪些
電磁波是怎么產(chǎn)生的 電磁波的激發(fā)原理




 一文解析電磁場與電磁波中復(fù)數(shù)的物理意義
一文解析電磁場與電磁波中復(fù)數(shù)的物理意義

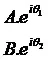










評論