使用聯想鏈條和幾何直觀，輔以從實際需求衍生概念的思考模式，詳解什么是傅立葉變換，為什么要做傅立葉變換等，幫助記憶和理解，目的當然是標題所說：讓你永遠忘不了傅里葉變換這個公式。另，這篇博客還從側面一定程度上回答了另一個問題：為什么要研究復數

本篇博客為形象展示傅里葉變換和歐拉公式與初等群論兩個視頻的筆記結合，希望通過此篇讓所有讀者對傅立葉變換有一個全新的認知，并且宣傳一波 3b1b 良心視頻系列！重塑對未知和知識的渴求

知乎相關問題鏈接，小伙伴們求點贊！沒有功勞也有苦勞啊！

歐拉公式與旋轉

在開始一步一步接近【傅立葉變換】前，先說一下群論 提前說明，此部分有地方會提到【群論】這個概念，但博主并不是要試圖把什么環、域、向量空間、代數結構、線性代數群、李群等等一大堆很抽象的概念灌輸給大家，我們只是為了利用群論的概念，加深或者說建立一個對【理解傅立葉變換】極度有幫助的直觀概念：指數函數（逆操作對數函數同理）是加法和乘法運算的橋梁，在自變量包含復數時表示旋轉。 以具體的一個例子來說: e^(πi)表示的是在單位圓上逆時針在旋轉180°這個變換。 等等，這不是排行世界上最偉大的十個公式第二名的歐拉公式（上帝公式）嘛？（BTW，我們今天的主角【傅立葉變換】排行第七，這陣容著實強大）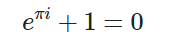

是的，這第一部分，捎帶，會帶你更進一步的重新認識這個公式的偉大

對稱性 symmetry

首先，假設我們有以下陳述：正方形是對稱圖形 那么從數學（定義 or 公式）角度上來說，怎么描述【對稱】這個概念呢？我們作為【人】，肯定會想，不就是看著左右一樣嘛？不夠嚴謹，不夠優雅，繼續深入，可以這么考慮： 你能對正方形做些什么，并且在這個操作后，保持正方形的形態和操作前相同我們把具有上述性質的操作都列出來，放在mi一起，如下面動圖所示（左右旋轉90°，旋轉180°，四個軸對稱，不變，這八個操作），就構成了一個有限群【對稱群】，更專業的叫法是【八階二面體群 Dihedral group of order 8】

有了上面的直觀理解，還有一個無限群需要了解，即【旋轉群】，表示的是所有旋轉操作，當然，因為角度可以無限細分，這個操作也是無限的，比如：順時針旋轉 此時，能總結出一個巧合的現象，按照順序進行上面8個操作的某兩個，恰好等同于8個操作中的其他的某一個（旋轉群同理），如下面的動圖所示，把這些組合放到一起，才真正的表達了【群】這個概念

很多不同的概念都能從對稱性和對稱性的符合構建得到，如下圖所示，其中，數字本身有兩種表達方式（操作），加法和乘法

對于【數】這個集合來說，加法對應數軸的平移變換（一個操作），乘法對應著數軸的伸縮變換（一個操作） 把這個數軸的概念拓展到平面坐標系，1D ? 2D。如果我們要把一個點，比如（1,0）移動到另一個點，應該如何操作？簡單的說，只需要先在橫軸方向上平移，再在縱軸方向上平移即可（核心思想類比于正方形的幾個操作） 同理，除了平移外，使用伸縮加旋轉也可以完成同樣的事情（將任意一點移動到另一個位置），伸縮是乘法顯而易見，但是旋轉怎么表示呢？（當然直接改變坐標軸的定義也是能做到的，例子就是極坐標系，但我們并不想這么做），我們構造以下思考鏈條：

考慮一個特例操作：一個點變到另一個點：（1,0）通過伸縮和旋轉到（-1,0），長度不用變，只需旋轉即可

此時，注意到了一個形式很有特點的定義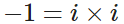：，-1 就是我們需要的目標位置，那如何從（1,0）出發進行兩次同樣的操作可以得到（-1,0）呢？（這個操作即?ii?這個虛數單位定義的操作）答案即：一個單位?ii?表示旋轉90°即可

更意外的發現，進行一次ii操作，如果是逆時針旋轉90°，正好會落在二維平面y軸的（0,1）與單位長度不謀而合

更大膽的假設，如果y軸自帶虛數單位，如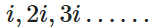，就有旋轉操作了，是不是就就能通過乘法來描述處在這個平面上的所有變換了

以上都是假設和推理，剝絲抽繭后，最關鍵的部分：如何使用單位i表示逆時針旋轉90°，并且給出了一種可能的映射規則，x軸平移表示伸縮，y軸平移表示旋轉，這樣就可以保證群的特性？（幾種操作一定可以組合成其他某個操作，有一個學名：保持群結構）i怎么可能表示旋轉呢？怎么看都像啊，此時陷入了死胡同，不妨換個角度來思考，旋轉到底是什么？旋轉，是沿著一個圓弧（有圓心，轉過的角度）運動的過程 如果你對泰勒公式非常熟悉，就可以通過一系列公式推導得到一個完美橋梁：【指數函數】，形如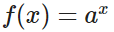 如果底數 a=e ，通過泰勒展開式，可以完成一個十分優美的變形，如下：

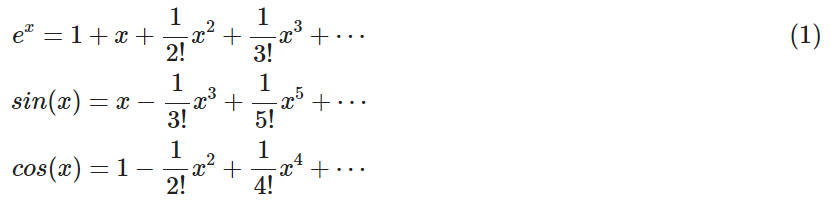
將 x=iθ帶入（1）式（這里的 θ是一個未知數，即自變量），整理項，移動，結合 cos(x) 和sin(x) 的泰勒展開式，還有虛數單位的定義 i=?1×?1 ， 有下列推導：

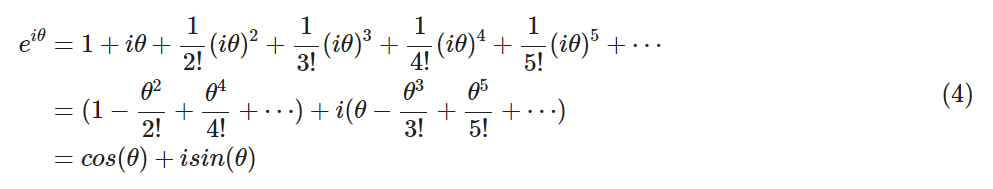
這個公式有什么用呢？可視化后，如下圖所示

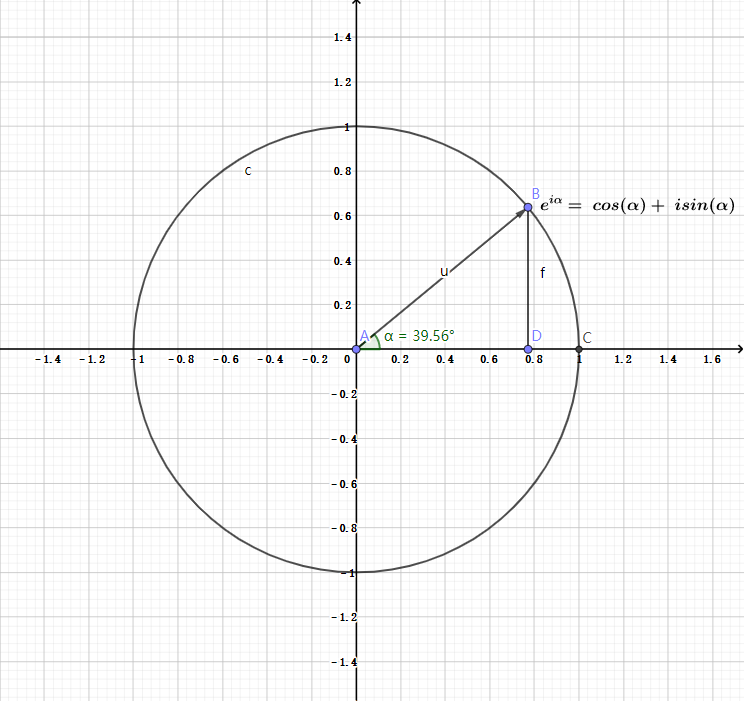
假設縱坐標自帶虛數單位 i （復平面），那么，sin(θ)為縱坐標（自帶虛數單位 i ），cos(θ)為橫坐標，則可以發現：e^(iθ)表示一個圓心在原點，半徑為1的單位圓（圖中是 α ，因為作圖軟件的限制，換不成 θ ，但不影響） e^(iθ)這個公式等價于一種旋轉，θθ為旋轉角的度數（統一單位，弧度制，即把°轉換成實數）θ=2π即為360°，是單位圓 我們已經優雅的找到了這個橋梁，接下來仔細研究一下它意味著什么

指數函數 Exponentiation

指數函數有一個非常重要的特性：加法變乘法，即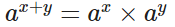 也就是說通過指數函數，可以做到使用平移變換來描述伸縮變換，這具體是什么意思呢？參考下面的動圖

上方的數軸，表示的是平移變換-1（左移一個單位） 和 2（右移兩個單位）（加法），下方的數軸將兩個數作為輸入，代入到一個指數函數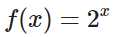中，對于函數來說，這個輸出值，就是兩次伸縮變換?（乘法），一次是收縮為原來的?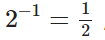，另一次是拉伸成原來的?倍 ? 注意，所謂可以變的意思是說，加法運算可以成立，意味著先往左平移1單位，再往右平移一單位，組合起來的左右就是往右平移一到位（-1+2=1, 群論的保持結構特性) ,? 而乘法運算成立也要滿足這個特性?? ?

復平面 Complex Plane

至此，構造復平面，把虛數單位ii加到縱軸上。我們就同時擁有了伸縮和旋轉，最關鍵的是，有了這兩個操作，我們同時也可以維持的群的特性（使用乘法） 如下面動圖所示，在復平面內，以指數函數為橋梁，實軸橫向平移對應伸縮，虛軸縱向平移對應旋轉

橫坐標紅線，橫向平移映射到伸縮操作的可視化 縱坐標虛數單位，縱向平移映射到旋轉操作的可視化，正為逆時針旋轉 現在使用的橋梁是底數為2的指數函數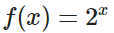，我們知道e^(πi)代表的半個圓周，我們希望把底數變成?e ,?這樣更加方便表達圓的概念 每走一個單位的縱向位移，在圓周上旋轉的圓弧長度就是1，參照下面的動圖，e^(πi)?恰好代表逆時針旋轉180°，并且落在的位置為（-1,0），這就是歐拉公式，或者說是歐拉公式的幾何直觀可視化

總結

這第一部分到底干了啥？其實就是想建立一個觀念（或者說常識）e^x 在復平面，或者說 x=ai（a為某個常數，就是弧度制的圓周長度）代表的變換是：旋轉如果你之前學過傅立葉變換，那么會明白為什么需要花費這么大篇幅來講這個，因為公式中， e^(iπ)那是可是相當重要的一部分啊

傅里葉變換

正式進入傅立葉變換的部分，老規矩，先做一下基本信息整理

什么是傅立葉變換

首先，還是先弄清楚我們理解的目標是什么 傅立葉變換（如果不加限定，這個詞對應的是連續傅立葉變換）
傅立葉級數 傅立葉變換還有很多其他的內容：離散時間傅立葉變換，離散傅立葉變換，傅立葉逆變換，快速傅立葉變換等，進一步的拉普拉斯變換，小波變換，z變換等

[ 公式表示 ]

傅立葉變換，變換作用是時域映射到頻域，公式是長這樣的：

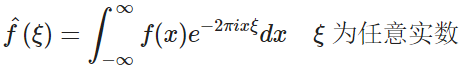
很多時候，這里的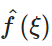會寫成 F(w) 或 F(f) 表示角速度或者頻率，當然后面的公式的量綱也需要對應的修改；后面的自變量 x 大多數時候都是寫成 t 表示時間。當然，他們表示的都是同一個東西 ?

[ 聯想鏈條 ]

既然是為了【理解】和【記憶】，那么我們還是需要定義一個聯想鏈條： 傅立葉變換 ? 分解聲音的過程 這么抽象實在是因為拆字法真的很難聯想出什么東西來（傅里葉？變換？嗯，很難的樣子），只能這樣了。 接下來就是精華部分：3b1b的傅立葉變換講解內的核心內容！在筆記完成后，會給出結合直觀理解的完整聯想鏈條，目的當然是【讓你永遠忘不了】嘍，點題！

【看到】傅立葉變換

[ 聲音的表示 ]我們是如何記錄聲音的呢？如果你測量的是揚聲器旁的氣壓，那么它會是一個隨時間以正弦函數形態不斷震蕩的圖像，一個標準音 A（下圖黃色），它的頻率是440Hz，表示每秒鐘振動440次，比它低一些的D（下圖紫紅），是294Hz，振動的慢一些。如果這兩個音同時發出，產生的氣壓隨時間曲線怎么決定呢？如下動圖，其實就是把所有時間點的振幅加起來

那么如果給你隨意一段隨時間變化的氣壓曲線，你如何找到這些原有的組成音符呢？這就是我們的目的，參考下面的動圖，感覺有點像是把一盤混好的原料分成組成它的單獨的顏色，感覺不那么容易吧？

下面就需要一步一步把這件事情做出來[ 可視化方法]首先，假設我們有一個每秒鐘3拍子的聲音信號（440Hz實在太快了），它的圖像如下（Intensity為強度，可以同理成氣壓），并且，我們只關注前面的4.5秒（即圖像中畫出來的部分）

1. 繞圈記錄法：同一事物的不同角度

千萬不要眨眼！下面是最關鍵的一步，是【看到】傅立葉變換的核心部分，如下面動圖所示

首先把黃色曲線纏繞到一個圓上，大小就是原本信號的振幅

圓周圍的圖像由白色的箭頭繪制而成，速度可變，上圖中的白色箭頭移動速度是每秒鐘轉過半圈（這個速度是對于下面的圓形圖像來說，每秒鐘在圓形圖像中轉半圈），對應上面的則是虛線表示一圈走到的位置，0.5拍子/秒

此時，有兩個頻率在起作用，一個是信號的頻率：3次震蕩/秒，另一個是圖像纏繞中心圓的頻率，為0.5圈/秒，第二個頻率可以自由改變，相當于一個變量，下面的動圖直觀的展現了纏繞速度變化時的可視化表現

從最開始的 0.79圈/秒（注意這里的速度是指繞單位圓的白色箭頭的滑動速度）一直變化到1.55圈/秒，再到最后的恰好是3圈/秒，和原來的信號3拍/秒相同，此時會出現一個非常穩定的圖像，我們可以理解成，同步，這個繞圈圖像記錄了原信號的幅值變化并且每一圈都相同（周期性） 其實，我們只是把一個水平的軸纏繞到一個單位圓上，并用另一個速度的記錄標尺（白色箭頭）來畫圖，從另一個角度（維度）來看我們的信號

2. 質心記錄法：新維度的特征提取

雖然新圖像挺好看的，但是現在感覺并沒法從中看出什么。也不盡然，我們直觀的發現，當白色箭頭記錄的速度在某些特定的值時，畫出來的圖形非常穩定，形態清晰。那如何表現這個特征呢？ 從兩個角度來思考 （1）自變量是什么？（輸入特征） 輸入是一個可變化的轉圈速度，既然可變，不妨把它看作自變量，即f(x)中的x （2）輸出（新的圓圈圖）有什么特征？（輸出特征） 觀察到，當圖像很混沌（沒有規律，混亂的）時候，圖像基本關于原點對稱；穩定時，其實是“頭重腳輕”的。描述“頭重腳輕”最好的方法當然是用【質心】（它描述了物體的空間分布特征） ，下面的動圖直觀展現了質心特征對圖像特征的描述能力（紅色點為質心）

考慮到質心其實是一個二維坐標，這里為了簡潔和直觀，取質心的橫坐標來表示質心的特征 【輸入（橫坐標）】?【進行采樣的（白色箭頭）的繞圈速度】 【輸出（縱坐標）】?【圓圈圖的質心位置的橫坐標】 按照上面的說明來記錄繪出圖像，記錄每個纏繞頻率（速度）對應的質心位置，參看下列動圖，隨著圖像的繪制到3圈/秒這個位置的時候，是不是感到似曾相識呢？

我們可以看到，新圖像的橫坐標寫的是【頻率 Frequency】，即纏繞圓圈的記錄速度，所以強烈建議看到頻率，想起速度，并且抽象為圍著圓圈跑的速度（個人感受，對理解【頻率】的概念有助益） 好！有了這個工具，先把它應用到兩個聲音的組合圖像中看看效果：（這是我最喜歡的一張動圖）

什么？還是沒看清上面的振動圖像如何變成圓圈圖的？看下面的動圖，纏繞圓圈速度為2圈/秒的白色箭頭將時間信息映射到圓圈圖中的的可視化。再次重復，白色箭頭以一定的速度（頻率，一秒幾圈）在上圖中向右橫移，同時，在下面的單位圓內被轉換成類似鐘表指針移動的圓圈運動，并記錄振幅，畫出圖像

BTW，圖形的一部分有點像動畫EVA中某個使徒的臉，帶給人一種詭異的儀式感。數學之令人敬畏，可能在這一刻熠熠生輝，刺的人睜不開眼[ 公式表示 ]大家也發現了，我們已經通過這樣一個纏繞機器完成了時域到頻域的轉換，總得來說，參看下面的動圖

這是一種【近傅立葉變換】，為什么是【近】，后面會提到。先考慮，那如何數學語言表達這個【轉圈記錄機制（工具 or 機器）】呢？

第一步：旋轉的表示

如下面的動圖所示，在這個工具中，非常關鍵的就是轉圈，即表達旋轉這種運動，根據第一大部分，這個橋梁，就是復平面，其背后的原理是指數函數結合泰勒公式

更進一步，指數函數中，以ee為底的函數有著特殊的性質，如下面動圖所示，ππ單位的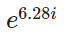就表示一個單位圓的360°旋轉，則表示的就是一秒鐘一圈的旋轉方程，感覺速度有點太快了，所以加一個 f?頻率，控制旋轉的速度?，圖中為?1/10 , 合起來表示一秒鐘十分之一圈

第二步：纏繞的表示

首先，依據下面的動圖所示，在傅立葉變換中，我們規定旋轉是順時針的（規定只是為了統一標準，并且有時候也會考慮書寫簡潔和方便計算），所以先加一個負號。假設原來的函數是g(t)，將兩者的幅值相乘就能得到纏繞圖像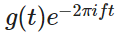，，可以說是相當機智了！

第三步：質心的表示

那如何表示質心這一概念呢？粗略想一下感覺挺難的，但是看起來很難的問題，有一種解決問題的途徑是【演繹推理】，先從簡單的特例出發，推廣到一般，最后證明正確性即可 考慮如何求一個正方形的質心位置，我們只需在邊框上取n個等距離分布的點，并且算這幾個點的位置的平均值。那么推廣到一般情況，也使用類似的采樣點的方式解決，如下面動圖所示（紫紅色的點即采樣點），得到

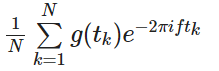
隨著采樣點的增加，需要使用積分來求解這個問題，如下面動圖所示，得到

最終步：整理積分限和系數

看到常數項系數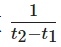，如果忽略表達倍數關系的系數，對應的含義也會發生變化，不再是質心，而是信號存在的時間越久，位置是質心位置乘以一個倍數，它的值就越大。參看下面的動圖，持續時長為3秒，那么新的位置就是原來質心位置的三倍；為6秒，就是原來的6倍

而去掉系數的幾何直觀動圖變為（紅色箭頭為去掉系數后的長度表示），最本質的區別是：可以使得最后繪制的圖像更集中在對應的頻率的附近，或者說在對應的頻率位置的值更大

繼續考慮上下限。我們知道，一般傅立葉變換公式的上下限是正負無窮，那它的幾何直觀是什么呢？參看下面動圖，其實就是看看信號持續時間無窮大是什么樣子的

說實話，這個動圖解答了我大學時代的一個疑惑，音樂文件不都是有時間長度的嘛，我就一直不懂，憑什么對負無窮到正無窮做傅立葉變換？原來真實情況是，負無窮到0，音樂結尾到正無窮，就像上面的動圖，其實都沒有振動幅值（電信號幅值）與之對應，再結合纏繞圓圈的思想：原來，從音樂開始到結束傅立葉變換和從負無窮到正無窮做傅立葉變換，是特么的一回事啊！（吐槽完畢）

補充

[ 相位 ]在表示質心的時候，我們只取用了x軸坐標，下面的圖中的藍色曲線就是縱坐標（y軸 or 虛部）的可視化,紅色曲線是橫坐標（x軸 or 實部）

那么相位是如何表示的呢？如下面動圖所示，其中紅色的部分為質心，長度為振幅大小，對應的角度就是相位

[ 原信號的長度 ]

再追根究底一些，因為之前已經提到過，假設我們的信號有4.5s。 那么考慮原信號的長度的變化呢？首先，假設信號的長度很長，那么纏繞圓上的線就會更多，每次接近穩定圖像質心的變化速度更快（即頻域圖像更加密集），參看下面動圖

那么對應的，如果原信號的長度縮短呢？如下面動圖所示，頻域圖像會更加稀疏。原因同理，當纏繞的內容少的時候，重心變化的速度也相應的變慢了

總得來說，基本就上述內容就詳細解釋了下面的現象：

時域的信號周期越長，那么頻域就越集中，越不容易發生混疊，越容易抽象出時間信號的周期性重復信息，此時自然而然的，周期性這個詞就出現了。 另外，可以自己思索一下，比如無窮時間的周期時域信號呢？又比如一個恒定振幅（一個電平）的時域信號呢？其實這里就給出了一個提示有關為什么傅立葉變換有那么多需要考慮的變形了，因為在纏繞這件事情發生的過程中，有幾種情況是特別的（這部分3B1B視頻并沒有講解，可能需要未來再更新了）

總結

講了這么長，至此全部結束。估計讀者都已經暈了，那么，在這里為【看到】傅立葉變換做一個總結，就來總得說說我們從頭到尾都干了些啥？參看下面動圖

（1）e^(πi)表示單位圓，添加自變量即可表示旋轉

（2）與原函數相乘纏繞到單位圓上

（3）為求質心的特征，進行積分計算

一步一步寫出傅立葉變換公式的聯想鏈條

一個逆時針旋轉360°畫成的圓 ?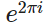

表示運動，需要原函數的自變量，時間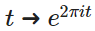

表示旋轉速度，需要自變量，頻率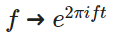

規定變換的采樣方向為順時針，加負號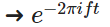

乘以原函數纏繞到單位圓并記錄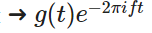（此處使用g符號標識原函數是為了和頻率符號區分

為了計算質心特征，積分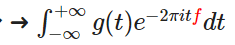

自變量為頻率ff，寫出函數表達式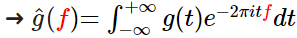

責任編輯：xj

原文標題：讓你永遠忘不了的傅里葉變換解析

文章出處：【微信公眾號：嵌入式ARM】歡迎添加關注！文章轉載請注明出處。